基于自适应增量调制的语音延时电路设计

陈 峰，陈嘉鹏，苏郁秋

（中国电子科技集团公司第58研究所，江苏 无锡 214035）

1 引言

普通的声音信号为模拟信号，要实现延时功能，须先用调制器将其转换成数字信号，经数字延时后，再通过解调器还原成模拟信号输出。

传统的PCM即脉冲编码调制，对每个采样信号的幅度进行量化编码，具有对任意波形量化的能力，但忽略了相邻样值的相关性，需要较长的码，结构复杂。DM（Delta Modulation）即增量调制，是对实际与预测的采样信号之差的极性进行编码，用一位码即可表示相邻抽样值的相对大小。自适应增量调制ADM（Adaptive Delta Modulation）是在DM上的一种改进，通过自动调整步距，使调制的信号失真更小，噪声更低。理论研究表明，在信号速率低于40kb/s时，ADM效果优于PCM，而且采用ADM方式的调制解调电路都相对简单[5]。

2 增量调制（DM）

增量调制是一种预测编码技术，它对实际采样信号与预测采样信号之差的极性进行编码，采用一位编码，如果实际采样值大于预测采样值则用“1”表示，如果实际采样信号值小于预测采样值则用“0”表示，接收端每收到一个“1”码就使输出上升一个Δ值，每收到一个“0”码就使输出下降一个Δ值，连续收到“1”码（或“0”码）就使输出一直上升（或下降），这样就可以近似地复制出阶梯波形，此时再用低通滤波器滤除其中的高频分量，即可还原出原始输入信号[4]。

DM存在量化噪声，通常有两种。一种为斜率过载（Slope Overload），是由于步距Δ值太小，以至于预测信号跟不上斜率较陡峭的模拟信号；另一种为一般量化噪声，又叫粒状噪声（Granular Noise），是由于在信号斜率较平缓的地方，编码输出序列为交替的“1”和“0”，如图1所示。

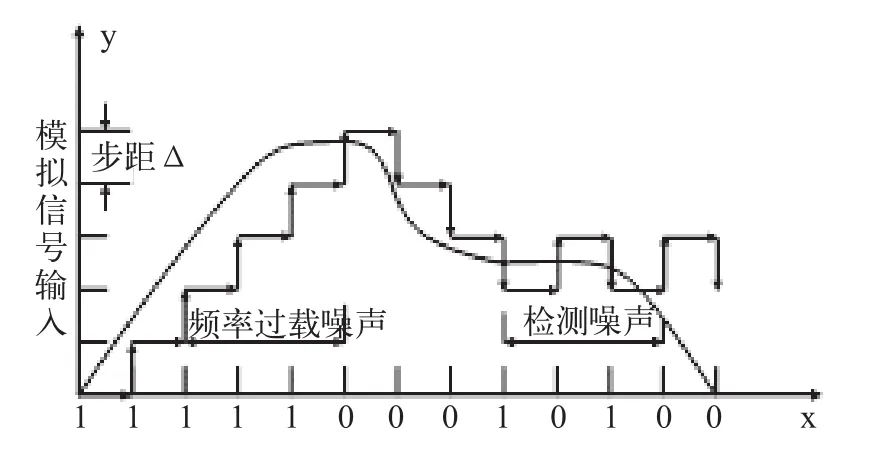
图1 DM量化噪声示意图

由图1我们可以看到DM系统的采样率必须足够高，如此不仅能降低斜率过载噪声，又能取较小的步距Δ值从而减小一般量化噪声。因此DM系统中的抽样频率要比PCM系统的高得多，称为过采样（远高于奈奎斯特速率）。由于较高的采样频率，对于DM系统的抗混叠滤波器的要求也较低。通常DM系统也不需要专门的采样/保持电路，因为进行量化的电路本身就要进行采样。

3 自适应增量调制（ADM）

由以上分析可知，在采样频率固定的情况下，选择合适的步距Δ值来同时减小斜率过载噪声和一般量化噪声是不可能的，增大步距Δ值虽然减小了斜率过载噪声，但却会增大一般量化噪声，反之亦然。因此有人提出自动改变步距Δ值的方法，在信号较陡时增大Δ值，在信号平缓时减小Δ值。

一种自适应方式是使量阶大小随信号幅度瞬时压扩，称为瞬时压扩增量调制，假如调制器输出为“1”和“0”，当输出不变时步距Δ值增大一倍，而当输出改变时步距Δ值减小一半。

另一种方式称为连续可变斜率增量调制（CVSD）。当输出中出现连续的“1”和“0”时，表明斜率出现过载，这时增大步距Δ值，当不出现连续的“1”和“0”时，步距减小直到最小。本文采用这种方式[1]。

4 系统及硬件实现

输入的音频信号x（t）经过二阶的抗混叠低通滤波器，将输入信号与预测信号进行比较，输出的高低电平由第一级D触发器进行采样作为编码输出，输出码流通过四个连续0/1判断送出一个信号进入到电流源中的音节积分器，从而调节步距Δ值的大小，而第一级触发器的输出控制电流源的极性，从而决定是对原信号增加步距Δ值还是减小步距Δ值。输入编码电路如图2所示[2]。

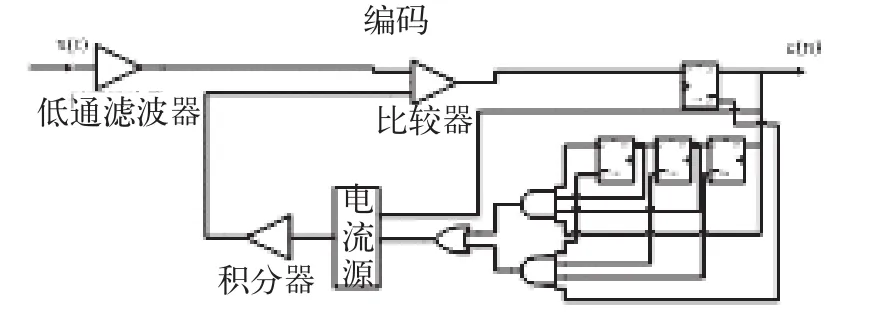
图2 输入编码电路

编码输出c(n)经过存储器形成延时，输出码流经过可变增量调制模块对积分器积分，最后通过一个二阶低通器滤除高频分量还原成原始输入信号。解码电路如图3所示。

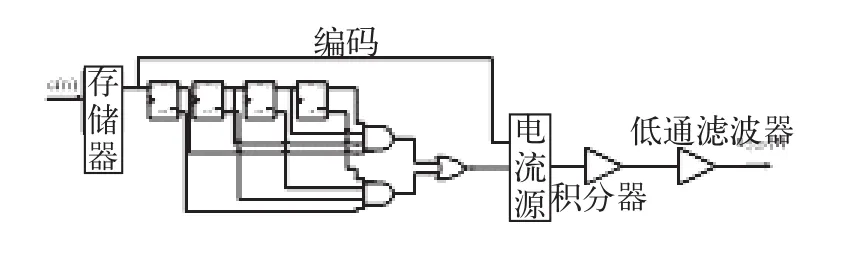
图3 解码电路示意图

图中积分器、低通滤波器由于没有带低阻抗负载，因此采用较为简单的两级无缓冲运算放大器就能满足要求。为了要提供足够的相位裕度，防止放大器自激，加入了补偿电容。为了提高速度，比较器在放大器基础上加大了偏置从而提高了速度。 图2、图3中电流源配合连0/1检测电路完成步距Δ值的自动调整，并将0/1转换成正向/负向积分。电流源电路如图4所示[3]。

图中Vin1开关与左边的R1、R2、C构成音节积分器I2，负责自动调节步距Δ值的大小，当预测信号无法跟上输入信号时，比较器将持续输出“0”或“1”，当触发器检测到连续四个“0”或“1”时，将把开关Vin1打开，通过电阻R1对电容C充电，使C上极板电压升高，因此镜像到输出端的电流Iout也增大，使步距Δ值增大，从而减小斜率过载失真；当预测信号可以跟上输入时，比较器将间隔输出“0”或“1”，Vin1关闭，电容上的电荷通过R2对地放电，电容C上极板的电压减小，镜像到输出端的电流Iout也减小，从而减小一般量化噪声。这里，我们选取R1=5K，R2=50K，C=100n，使得放电时间常数为R2×C=5ms。

图4 电流源电路示意图

图中Vin2为第一级触发器输出，完成对积分器充/放电选择的功能。

预测信号产生电路如图5所示。

图5 预测信号产生电路示意图

Iout为电流源输出电流，积分电容为C，REF偏置为电源电压的一半，x(t)即为预测信号输出。

假设输入的是正弦函数，A为振幅，ω为信号角频率，f为对应信号频率，Δ1为步距， fs为采样频率，T为对应的采样周期，则系统能跟踪的最大斜率为Aω=Δ1fs。

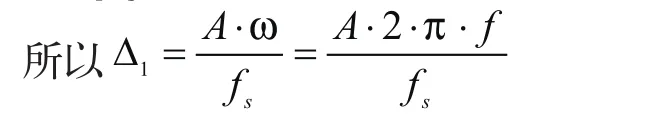
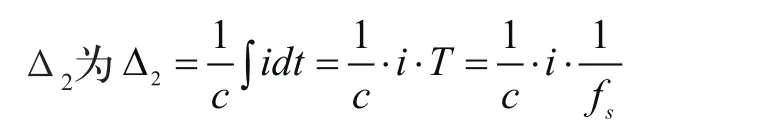
因此，为了不产生失真，应该选取合适的电流和电容值以满足以上等式。

图6为实际ADM调制解调使用Hspice的仿真波形图，上面的曲线为预测信号的输出，可以看到在电源电压一半的地方即信号斜率较陡处，步距Δ值较大，而在波峰波谷斜率较平缓处，步距Δ值较小，且含有一般量化噪声；下面的曲线为预测信号经过低通滤波器滤波后的波形。在输入信号第二个周期用four函数计算的谐波失真小于0.5%。电路采用0.5μm工艺流片，典型工作电压为5V，实测延时后的噪声电压为-88dBV，总谐波噪声+失真＜0.5%。

图6 ADM调制解调仿真波形图

5 结论

以上分析了自适应增量调制解调的原理，通过流片验证，其输出的音频信号品质较高，具有较为优良的性能。通过对电路添加适当的外围器件可以使其产生各种不同的混响效果，因此可以广泛应用在如扩音器系统、卡拉OK系统、CDDVD、车载音响、调音台等需要混响的场合，产生较高品质的混响效果。

[1] Continuously Variable Slope Delta Modulation: A Tutorial[P]. MX-com Inc,1998.

[2] Digital Coding of Waveforms: Principles and Applications to Speech and Video[M]. N. S. Jayant and P. Noll, Prentice-Hall, Englewood Cliffs, N. J., 1984.

[3] Phillip E.Allen Douglas R.Holberg 著，冯军，李智群，译. CMOS模拟集成电路设计[M].北京：电子工业出版社，2006.

[4] 樊昌信，詹道庸，等. 通信原理[M].北京：国防工业出版社，1995.

[5] 轩素静，邹玉斌. 自适应增量调制的仿真实现及性能分析[J].计算机测量与控制，2003，11.