探讨多原子分子的Schrödinger 方程组的严格解析解法——以血红蛋白电离能的计算为例

任爱娣，王文信

( 海军工程大学( 天津校区)，天津 300450)

众所周知，许许多多科学家都研究过多原子分子Schrödinger 方程组［1］

其中:方程(1)是固定核的位置时电子运动方程;E 为所需要的能量;方程(2)是核运动方程;ε 为总能量;M 和N 分别代表原子核和电子的总数;V 系静电势能。

可见，方程组(1)和(2)的解是十分重要的。Bohr.N，Hartree.D.R ，Fock.B.A，Oppenheimer.J.R 和Born.M 等［1-5］的研究成果一直沿用到今天，极大地丰富了人类的知识宝库。唐敖庆先生在文献［1］中只是给出双原子分子Schrödinger 的近似解，虽然已经给出双原子分子、三原子分子和四原子分子的Schrödinger 方程组的严格解析解［6］，但是，这并不意味着能够给出所有多原子分子Schrödinger 方程组的严格解析解。那么对于任意一个多原子分子Schrödinger 方程组究竟有没有严格解析解呢? 至今没见答案。为了能够找到这个答案，笔者发展了我国著名科学家唐敖庆先生在文献［1］中的方法，在超球坐标系中，首先获得了电子运动方程的严格解析解。从所得解中找到了原子核运动的所需的能量，自然就能够求得原子核运动方程的严格解析解。又从所得解中找到总能量和电离能的计算公式，就能够计算血红蛋白分子的电离能，从而验证该探讨是成功的。答案就自动产生了。

1 电子运动的Schrödinger 方程的严格解析解

对于电子运动的Schrödinger 方程(1)，用超球谐法［7-9］可以得到它的解析解

其中:rij、r0ij和Rij分别表示原子核i 到电子j，电子i 到电子j 以及原子核i 到原子核j 之间的距离;Zj系原子序数;N0=1，Nj=N0+Z1+…Zj;Ω 是球极角和超球角的集。

为了能够方便地应用所得到的严格解析解(3)，需要进一步剖析它。首先看它的静电势能V。从式(5)可以看出，它是各个电子之间、各个原子核之间和原子核与电子之间所形成的静电势能之和，其中包括各个电子绕自己的原子核运动所产生的静电势能之和V*，即V*⊂V。显然V*与核间距Rij的变化无关，而V-V*则相反，它们的变化就意味着核间距Rij的变化。由此就可以把静电势能V 分解成

其中V*与核间距Rij的变化无关，而V-V*则相反。

既然静电势能V 可以写成2 项之和，它们在超球谐中的展开式自然也能够写成2 项之和，即

由于V*与核间距Rij的变化无关，所以它在超球谐中的展开式与核间距Rij的变化也无关，而则相反，它的变化就意味着核间距Rij的变化。类似地，也能把式(6)一分为二:其一与核间距Rij无关;其二则相反，即

其中:

能量公式改写成式(10)后，其意义更加明。先看第2 项，由于α*与V*有关，与核间距Rij变化无关，V*是各个电子绕自己的核运动所产生的静电势能之和，所以-α2*/2 所表示的能量与V*有关，与核间距Rij变化无关。第1 项则相反，E*变化意味着核间距Rij变化，也就是说，E*变化决定着核间距Rij变化，可见，E*应该是核间距Rij变化所需要的能量。

E*是核间距Rij的变化所需要的能量，而核间距Rij的变化是由原子核运动决定的。那么原子核是如何运动呢? 根据熟知的Born-Oppenheimer 理论［1］，由于原子核的质量比电子大103～105倍，电子速度比原子核快得多，这就使得当核间距任意微小运动时，迅速运动的电子都能立即进行调整，建立起与变幻后的核力场相应的运动状态;原子核相对于电子来说，速度慢得多，好像是不运动，其实也可能在运动，不可能绝对不运动。既然原子核也在运动。就需要去解原子核运动的Schrödinger 方程(2)。

2 核运动Schrödinger 方程的一种解法

为了能够解Schrödinger 方程(2)，需要求其折合质量。

图1 四核坐标示意图

1)折合质量的求法

为了求其折合质量取坐标原点为O 点，M 个原子，核A，B，C，D….的坐标向量分别是OA=R1，OB=R2，…，OC=RM( 见图1)，向量R*1的终点为质心的坐标，它们质量分别为m1，m2，…，mM，并且满足

其中m*=m1+m2+…+ mM。把上面的式子写成矩阵形式

再由式(11)和复合函数求全导数法，解得速度之间的关系为

其中:v*和vi分别为质心和第i 原子核的速度; vij为第i 与第j 个原子核的相对速度。式( 12)的两端同乘一个三角矩阵可得

和其转置矩阵

从式(12)～(14)和Laplace 算子▽2易知，动能T 可以表达为

它们的折合质量或约化质量分别为

其中:R*2=R1M;R*j= |R*j|;θij是向量Ri+1i与向量Rj+1j之间的夹角;tj为向量模间的比例系数，即

为了解多原子分子核运动的Schrödinger 方程(2)，需要分解它。

2)多原子分子核运动的Schrödinger 方程的分解

用分离变量法式(17)可化成下面等价的方程组［1］:

其中:方程(19)是质心平动的方程，ε1表示其所的需能量;方程(20)是核相对运动的方程，ε-E-ε1表示核相对运动所的需能量，也就是核间距变化所的需能量。有趣的是，在分析式(10)时已知核间距变化所需要的能量为E*，所以二者应该相等，即

把式(10)代人式(21)消去E 得到

把式(22)代入方程(20)，方程(20)就转化为

这样以来，只须解方程(19)和(23)就可以了。

3)多原子分子核运动的Schrödinger 方程的解析解

①对于质心平动方程(19)，ε1是未知能量，应用式(42)，方程(23)的解是

当l1=0 时为常数，质心只能作平移运动［1］，无旋转运动，于是质心平动方程(19)的严格解析解为

其中C 是常数。再由式(43)和(44)得

再把式(24)和式(26)代入式(18)，得到方程(17)通解

其中Cj为归一化系数。至此，就找到了多原子分子Schrödinger 方程组(1)和(2)的严格解析解，其完整表达式就是式(3)和式(29)。

3 多原子分子解析解的重要性质

为了了解严格解析解(3)和(29)的重要性质，首先需要剖析它的各个因子。

3)Jacobi 多项式F( -nj，nj+λj-1+3j/2-1，Lj+3/2|y)和Kummer 函数F(1，2，ρ1)及F( l2+1，2l+2，ρ2)显然都是连续、单值、可导和平方可积的函数，并且该Jacobi 多项式还能够形成完全正交基函数的集［8，11］。于是，ω( nj，Li，λj-1|y)和YλNu( Ω)都是连续、单值、可导和平方可积的函数［11］。

从1)～3)的论证可知，φ( r，Ω)和ψ( ρ1，ρ2，l2)都符合波函数的标准化条件［2-3］，所以它们都是多原子分子的品优波函数［2-3］，并且利用它们还能够求得其核间距。

4 多原子分子核间距的计算方法

由于核间距|Rij|的变化是由原子核运动决定的，所以确切的说，核间距是随机变量，是不能够十分准确确定它的值的。但是，根据需要，人们还得去求它，测它。人们之所以能够求到它，测到它，说明它出现的概率是很大的。因此，可以利用原子核相对运动的Schrödinger 方程的解析解(29)来求。

解析解ψ( ρ1，ρ2，l2)既然是个品优波函数，根据波函数统计规律，ψ( ρ1，ρ2，l2)应该具有表示微粒运动几率的功能。具体说来，以原子核A 为球心，以为ρ2半径，另外一个原子核C 为动点，分布函数为［2］

它表征发现该动点处于单位厚度的球壳的几率［2］。当D 极大时，dD/dρ2=0，即

其中，Cj0是相应的常数。这样以来，就可以用式(30)求出极值点ρ2=ρ*，这说明ρ2=ρ*的几率极大，也就是说，ρ2=ρ*的可能性极大。再由式(25)可知

这就表明，R1M=ρ*/(2β2)的可能性也极大。正因为如此，无论是测量核间距|R1M|，或是计算核间距|R1M|，得到ρ*/(2β2)的可能性极大。这就是把ρ*/(2β2)当作核间距|R1M|的值的理由。再用式(11)和(16)可以求出其它的核间距|Rij|的值。在这里自然需要假设各个核间距|Rij|的变化是同步的，即各个核间距|Rij|变化时，它们的比值保持不变。从式(30)又可以看出，这些核间距|Rij|的值不仅与β2有关，而且与Kummer 函数也有关。理所当然，在某一个核间距Rij的值很大时，就意味着分子的瓦解。那么瓦解时所需要的能量是多少呢?

5 多原子分子的分解所需要的能量和总能量

为了求总能量，先求出多原子分子核相对运动所需要的能量。

1)多原子分子核相对运动所需要的能量

由式(22)知

再由式(31)知

于是

利用核相对运动所需要的能量就可以求得多原子分子的分解时所需的能量。

2)多原子分子的分解所需要的能量

在式(32)中，β2可由式(28)得到，即

3)质心平动所的需要的能量

从式(25)的第1 式能够求得质心平动所的需要的能量

特别地，当质心作匀速平动或静止时，由方程(2)可以得到ε1=0。

4)核运动所需要的能量

由式(32)和(33)得

式(34)表示质心平动所的需要的能量ε1和核相对运动所需要的能量E*之和，也就是核运动所需要的能量。下面就该求出多原子分子电子运动需要的能量。

5)多原子分子电子运动需要的能量

利用能量公式( 式(3)第2 式)就可以来计算电子运动需要的能量:

也可以用式(10)来求电子运动需要的能量E，即

再由式(32)，上式变成

用式(35)来计算电子运动所需的能量，可以省去积分运算，比较方便，由此还可以去求总能量。

6)多原子分子的总能量

从式(21)可知总能量

利用式(32)～(35)得

式(36)就是总能量ε 的计算公式。利用式(35)和式(3)第2 式还可以得到

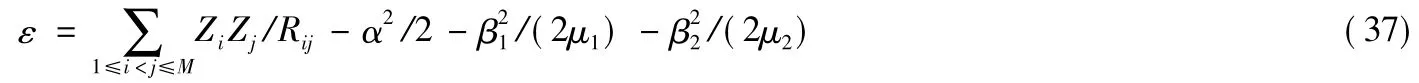
由多原子分子总能量ε 的计算式(37)，就可以导出其电离能的计算公式。

7)多原子分子电离能的计算公式

对于多原子分子，共有N 个电子。不妨选中一个原子的一个外层电子，可用式(36)或(37)来计算总能量ε。当这个原子的一个外层电子丢失后，剩下N-1 个电子。也可以用式(36)或(37)重新计算其总能量:

它的电离能应该等于丢失电子前、后的总能量之差Δε，利用式(37)和(38)得

当多原子分子在丢失电子时，在那一刹那间，分子来不及调整结构，也就是说，结构是不变的，于是

把式(40)代人(39)式中得

式(41)就是多原子分子的一个外层电子丢失前、后的总能量差，即多原子分子电离能的计算公式。还可以看出，它也是被指定的原子的一个外层电子丢失前、后能量的差，即被指定原子的电离能的计算公式。也就是说，它既是分子电离能的计算公式，也是原子的电离能的计算公式。对于它的应用，举例说明如下。

金属铝的晶胞是由4 个铝原子构成，Z=13，N=52，m=26.915 4。计算铝的晶胞的电离能，其结果见表1。

表1 铝的晶胞电离能Δε(ev)和Lagueree 系数n 的关系

从表1 的第1 列能够看出，金属铝的晶胞电离能与其实验值8.986 ev 很接近［2］，说明所得的解析解具有一定的可靠性。另外，从表1 还能够看出，随着Lagueree 函数的次数n 增大，电离能而减小，说明电离能与Lagueree 函数的次数n 等环境条件有密切关。

血红蛋白分子［5］Fe4C3032H4816O872N780S8有9 512 个原子核，原子序数分别是:28，6，1，8，7，16，共有38 076 个电子。现在不妨选中血红蛋白分子的碳原子的一个外层电子，应用式(41)计算，结果见表2。

表2 血红蛋白分子电离能Δε( -kj/mol)和Lagueree 系数

从表2 能够看出，血红蛋白分子的电离能与Lagueree 函数的次数n 等环境条件有关。随着Lagueree 函数的次数n 增大而减小。从表2 还可以看出，血红蛋白分子的电离能很小很小，也正因为如此，它很用容易失去电子，这就是很多病的病根和病原［2］。

值得注意的是，在寻求解析解(3)和(29)的过程中，引用了式(42)～(44)，它们来自下面的定理。

定理已知Schrödinger 方程

其中E 表示未知能量，则其解析解为

其中l 是正整数，F( l+1，2l+2，ρ)为Kummer 函数，

这个定理笔者已经证明过，它是正确的［6］。这就说明笔者的探讨是成功的。

［1］唐敖庆.量子化学［M］.北京:科学出版社，1982: 2-11.

［2］徐光宪，王祥云.物质结构［M］.北京:高等教育出版社，1959:3-55，589-591.

［3］潘道曀，赵成大，郑载兴.物质结构［M］.北京:等教育出版社，1982:5-101.

［4］周公度，段连运.结构化学基础［M］.北京:北京大学出版社，1997:392-396，429-434.

［5］维达多夫.生物学与量子力学［M］.李培廉，李景惠，张维华，译.北京:科学出版社，1990，40-49，36-37.

［6］任爱娣，王文信. 探讨双原子分子Schrödinger 方程组的严格解析解［J］.四川兵工学报，2011，32(11):144-148.

［7］任爱娣，王文信.探讨多电子原子和分子Schrödinger 方程的严格解析解［J］.分子科学学报，2011，27:291-296.

［8］DENG C，ZHANG R Q，FENG D C.Solution of Atom and MolecularSchrödinger Equation Described Hyperspherical Coordinates［J］.J Quant Chem Approach to the Description of Using Hyperspherical Coordinates，1993，45:385.

［9］KINRK D L.Approach to the Description of Using Hyperspherical Coordinates［J］.Chem Phys，1974，60:67.

［10］刘式适，刘式达.特殊函数［M］.北京:Meteorologic Press，2002:597.

［11］江泽坚，吴智泉.实变函数论［M］.北京:高等教育出版社，1961:137-138，157-159.