一种改进的嵌入式零树小波编码方法

胡静涛，陈 卫

( 陆军军官学院5 系，合肥 230031)

图像数据压缩就是通过减少图像数据之间的冗余来减少数据量，从而达到减少存储空间，提高传输效率的目的［1］。上个世纪90年代后，图像压缩编码研究取得了一系列的阶段性新成果，基于零树的编码法首先由A.S.Lewis 和G.Knowles 提出［2］，其特点是根据小波系数在同方向子带中的相似性，利用一种称为小波树的树形结构来组织小波系数，使其能去除频域和空间域中的相关性［3］。接着Shapiro 结合比特平面编码方法设计了一种更好的零树编码方法—嵌入式零树小波编码( EZW)方法［4］，Shaprio 提出的嵌入式零树小波算法，它有效地利用了小波系数的特性，实现了图像的可分级编码。但也存在算法时间长和空间复杂度过高的缺点。

1 嵌入式零树小波编码

1.1 嵌入式编码

嵌入式编码即编码器把待编码的比特流按照重要性的不同进行排序，根据目标码率要求随时结束编码;对于给定的码流，解码器也能够在任意点结束解码，并可以得到相应目标码率的解码图像。从均方误差的角度看，幅值较大的系数所包含的信息量相对较大，一旦丢失引起的失真度也较大。为了减少失真度，在处理过程中优先编码和传输幅值较大的系数［5］。

嵌入式编码即将变换系数按照幅值从大到小排列，首先传输幅值最大的变换系数的位信息，也就是最重要的信息，然后传输次重要系数，最后传输的系数最不重要［6］。在传输前所有的变换系数用二进制的方式表示，如图1。

1.2 零树小波编码

1.2.1 小波树结构

小波分解后，各个分辨率子带中的系数并不是完全独立的，图像的子带之间有结构的自相似性，具有结构冗余［7］。各分辨率子带系数间有如下的对应关系［8］。

1)除了最高分辨率的子带外，每一个小波系数都与同空间方向的高一级分辨率等级内的一组小波系数相联系;

2)系数之间比较，处于低分辨率等级子带的系数称为父系数，在同一方向高一分辨率等级，并且与其在相同空间位置的所有系数称为它的子系数;

3)对于一个给定的父系数，与其在同空间方向，且分辨率等级更高的所有子系数，称为它的子孙系数;

4)除了最低分辨率的子带，所有的父系数都有4 个子系。

图1 按幅度排序信息的二进制表示

图2 为一个采用上述方式进行三级分解的小波树。其中箭头方向表示，由父系数子带指向子系数子带［9］。

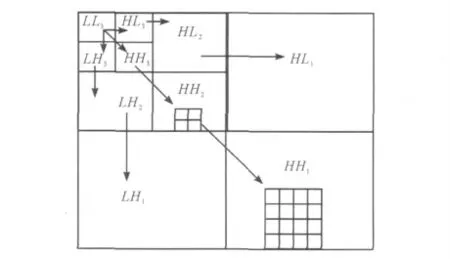
图2 子带间的父子关系

在对小波系数编码时，对小波系数的扫描应保证没有子孙系数在其父系数之前被扫描。对一个N 级分解小波变换，扫描从最低频子带LLN开始，然后扫描HLN，LHN，HHN，再扫描下一分辨率等级的子带HLN-1，LHN-1，HHN-1，如此继续，最后扫描HH1。如图3 所示。

图3 小波系数扫描顺序示意图

要想在解码端恢复出原图像，需要传送小波系数的排序信息和位信息。如果每个小波系数的排序信息和位信息都要传送的话，这样需要的数据花销是非常大的，根本就达不到压缩的目的，但是零树结构的存在解决了这个难题［10］。

零树的数据结构:对于一个小波系数xi，如果对于一个给定的门限T，＞T，则称该小波系数为重要系数，否则为不重要系数［25］。正重要系数用符号POS( positive)表示，负重要系数用符号NEG( negative)表示。如果该系数为不重要系数，但是其子孙系数中有重要系数，则该系数为孤立零点，用IZ( isolated)表示。如果该系数为不重要系数，但是其子孙系数中没有重要系数，且该系数的父系数为重要系数，则该系数为零树根，用ZTR( zerotree)表示，该系数和其子孙系数就形成了一个零树，在低分辨率上的那个小波系数被称为母体，是树根;在高分辨率上同方向相应位置上的那些小波系数称为孩子。通过这种零树结构，巧妙地编码，使用于描述重要系数的位置信息大大减少。

1.2.2 逐次逼近量化

在EZW 算法中使用的是逐次逼近量化( successive approximation quantization，SAQ)方法。逐次逼近量化的主要思想是，通过逐次使用阈值序列T0，T1，…，TN-1来判断小波系数的重要性，并确定其类型码和幅值码［11］。

在整个编( 解)码过程中，始终存在着两个过程—主扫描和辅扫描，它们交替进行，逐次提高量化精度。主扫描对应一张不断更新的主表，辅扫描对应一张不断更新的副表。通过这两个过程对重要系数、零树根和孤立零点构成的重要图进行编码，。实质上是对重要系数的位置和幅值编码。

2 EZW 算法的不足

虽然EZW 算法存在许多优点，算法简单，编码效率高。但是也存在着一些不足，主要表现在以下几个方面［5］:

1)在编码的过程中要形成许多棵零树，每生成一棵零树需要对数据扫描两遍，而且每一棵零树必须要在前一棵零树生成之后才能生成，造成编码效率低。对于一个小于阈值T的小波系数，为了判断其是孤立零还是零树根，必须对其所有后代系数进行扫描，势必增加编码时间，导致编码速度较慢。

2)通过前面的分析我们知道，经过小波变换后的系数重要程度不同。低频系数重要，而高频系数相对不重要。但是EZW 对所有频域不加区分，进行同等重要程度的编码，没有充分利用小波变换后系数的特点。。

3)在EZW 算法中树间存在大量的冗余，但是EZW 算法没有利用树与树之间的关系来减小树间冗余。

4)同一子带中相邻系数之间有一定的相关性，在高频系数中表现的尤为突出，通过子带的集合可以进一步地压缩数据。但是EZW 算法并没有对这种相关性进行充分的利用。

3 EZW 算法的改进

3.1 频率优先性

根据小波变换的理论可知，一幅图像经过小波变换后虽然其数据和总能量没有减少，但是其能量分布产生了比较大的变化。在低频系数子带中聚集了原始图像的大部分能量，高频系数只占有图像的一小部分能量。本文中的改进算法是把高频子带系数和低频子带系数分开处理。针对低频子带系数，单独对其进行无失真编码，采用差分脉冲编码调制( DPCM)，对编码后的码流再进行熵编码，进一步压缩码流，提高压缩效率。

DPCM 预测编码的系统原理框图［12］，如图4。

图4 DPCM 原理图

3.2 重要子带编码［13］

在原始嵌入式零树编码中，为了找到重要系数和确定零树根的位置，为了确定一个小波系数是零树根还是孤立零，往往需要扫描整棵四叉树和大量重复的扫描，时间复杂度高，同时消耗了大量的内存。

如果在扫描中事先就能确定重要系数可能存在的位置，只对重要系数存在的子带进行扫描，对不存在重要系数的子带不扫描，这样将在一定程度上减少扫描时间，提高压缩速度。由小波变换原理我们可以知道，一幅图像经过N 级小波变换分解后，形成了3N+1 个子带。首先，寻找每个子带中的小波系数的最大值。即IK(1，2，3，…，3N+1)中小波系数的绝对值的最大值tK，其中1 ＜k ＜3N+1。图5 给出3 级图像小波分解后的每个子带系数绝对值的最大值的示意图。

第一次扫描时确定初始阈值T0，其确定方法与原始EZW方法相同。对于每一个子带将其绝对值最大值tK与T0进行比较，若tK＞T0，则该子带称为重要子带;若tK＜T0，则该子带称为不重要子带。开始扫描时，仍然按照morton 扫描顺序进行扫描。在整个编码中用p 表示正重要系数，n 表示负重要系数，t 表示不重要系数，i 表示非重要子带。当扫描时发现tK＜Ti时，用i 来表示这个不重要子带，同时不用再扫描该子带，直接扫描下一个子带;当tK＞T0时，用p 表示正重要系数，n表示负重要系数，t 表示不重要系数，i 表示非重要子带。

图5 子带系数最大值示意图

3.3 熵编码

对高频系数编码后形成的码流进行熵编码，减少数据量，本文采用霍夫曼编码。

综上所述，整个改进算法的流程如图6。

图6 改进算法的流程

4 实验仿真

为了更直观地说明算法的有效性，本文对改进算法进行实验仿真。

实验环境:Windows XP 系统，内存1G，Matlab7.0。

测试图像为Matlab7.0 中的测试图像westconcordorthophoto。

对图像采用db9/7 小波基对图像进行3 级分解与重构。

图7 测试图像westconcordorthophoto

仿真图片对比∶压缩比20∶1。

从上面得到的实验图像表明:

1)改进后的EZW 算法重构图像的质量较高，主观视觉效果较好，不产生任何方块效应;

2)在低码率时，改进算法的重构图像质量优于原EZW算法。

［1］刘峰.视频图像编码技术及国际标准［M］.北京:北京邮电大学出版社，2005.

［2］Lewis A S，Knowles G. Image compression using 2 - D wavelet transform［J］. IEEE Trans. On Image Processing，1992，1(2):244-250.

［3］王文波.基于小波的图像压缩编码［D］.成都:电子科技大学，2009.

［4］Shapiro J M. Embedded image coding using zerotrees of wavelet coefficients［J］. IEEE Trans.On Signal Processing，1993，41(12):3445-3462.

［5］成礼智，王红霞，罗永.小波的理论与应用［M］.北京:科学出版社，2004.

［6］王向阳等.基于自适应小波变换的嵌入式图像压缩算法［J］.微电子学与计算机，2005，22(2):121-123.

［7］李亮.基于小波变换的静态图像压缩编码研究［D］.大连:大连交通大学，2009.

［8］张春田，苏育挺，张静.数字图像压缩编码［M］.北京:清华大学出版社，2006.

［9］刘学锋.基于小波零树的嵌入式图像编码技术的研究与改进［D］.西安:西安科技大学，2006.

［10］薛冰. 嵌入式零树小波编码算法的改进与应用研究［D］.成都:电子科技大学，2008.

［11］陈冬，张田文，李东.位渐进逼近量化的EZW 改进算法［J］.哈尔滨工业大学学报，2010，42(5):779-783.

［12］姚敏，赵敏.改进的高效EZW 遥感图像压缩方法研究［J］.电子科技大学学报，2009，38(4):525-528.

［13］雷梅梅，余谅. 一种改进的嵌入式小波图像编码算法［J］.计算机工程与科学，2010，32(10):59-62.