飘带伞弹系统结构参数对弹道落点特性影响

王顺虹，董永香，段相杰

(1.中国空空导弹研究院，洛阳 471000;2.北京理工大学 爆炸科学与技术国家重点实验室，北京 100081)

超音速减速伞是一种应用较广泛的减速稳定装置［1，2］。一种由刚性伞帽和柔性飘带组成的飘带伞与常规柔性减速伞的气动特性及弹道特性都有所不同，刚性伞帽无需充气过程，在子弹被抛出的瞬间便能展开并将飘带拉直，获得较大阻力使子弹减速，同时为子弹提供稳定力矩，进入稳定的下落状态。常规柔性减速伞弹道大致分为自由坠落段、拉直段、充气段和稳定下降段［3］。应用常规柔性减速伞弹道模型来研究该飘带伞弹道显然不合理，再由该飘带伞中弹伞间距较小，伞帽直径一般也小于子弹口径，需考虑伞弹气动耦合效应，伞弹系统结构参数对伞弹气动弹道特性的影响较大。因此建立适用于该飘带伞弹系统的弹道模型，研究伞弹系统结构参数对弹道特性影响规律显的尤为重要。

在伞弹系统稳定下降段，可近似认为伞轴与来流方向重合，基于该假设，建立了单刚体五自由度伞弹系统弹道模型，并基于Matlab/Simulink 仿真工具，开发了对应伞弹系统结构参数等输入量分析弹道特性的气动弹道仿真平台。在试验数据对该平台校验基础上结合正交试验法分析了伞弹系统结构参数对弹道落点特性的影响。

1 飘带伞弹系统弹道模型建立

伞弹系统的运动是一个非常复杂的过程，其受力状态、环境参数、系统外形与姿态及随机参数等都很难精确地建立数学模型［2］。对于子母战斗部中的伞弹系统关注的主要是子弹的运动特性，假设在稳定下降段伞轴与来流方向重合，伞弹链接为光滑球铰链，飘带伞对子弹的作用可简化为一个与来流方向相反的拉力，这样可用子弹的受约束五自由度( 不考虑子弹绕对称轴的旋转)空中运动方程组来近似描述伞弹系统的二刚体运动，子弹受力图如图1 所示。将伞帽和飘带视为具有飘带和伞帽质量之和的质点，沿来流方向应用动量定理有

式中:Ts为子弹对飘带的拉力;Rs为飘带伞所受到的空气阻力;ms为飘带伞质量;θ 为弹道倾角。

根据牛顿第一定律:飘带伞对子弹的拉力T= -Ts，则有

将飘带伞对子弹的拉力加入弹体空间运动方程组［4］，便可得到伞弹系统单刚体弹道模型。其中子弹质心运动的动力学方程标量形式为

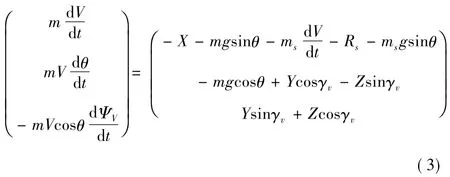
飘带伞拉力对子弹也产生了力矩的作用，则子弹绕质心转动的动力学方程为

子弹运动学方程和几何关系方程不受飘带伞拉力影响，相应的方程组与不受约束弹体空间运动方程组相同。

子弹质心运动的运动学方程

子弹绕质心转动的运动学方程

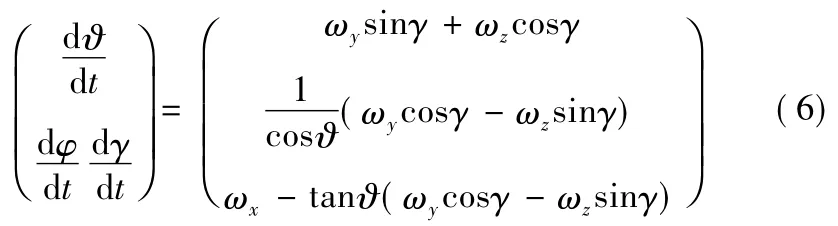
几何关系方程

弹道模型中，α，β 为子弹的攻角和侧滑角; γ，φ，ϑ 分别为子弹的滚转角，偏航角和俯仰角; ψv，γv，θ 为弹道倾斜角，弹道偏角和弹道倾角;a 为弹伞间距。X，Y，Z，Mx，My，Mz为速度坐标系下的三方向力和弹体坐标系下的三方向力矩。

图1 子弹受力图

2 基于Matlab/Simulink 的伞弹系统弹道模型模块化建模

按照模块化建模的思想，把伞弹系统弹道模型按功能分成气动计算模块和弹道解算模块，如图2 所示。其中气动计算模块又分为子弹气动参数计算和飘带伞气动参数计算两个子模块;弹道解算模块分为质心运动动力学、绕质心转动动力学、质心运动运动学、绕质心转动运动学、几何关系五个子模块，如图3 所示。

图2 伞弹系统弹道模型

子弹的气动参数计算子模块根据文献［7］中的弹丸气动参数工程估算公式建立，先计算子弹的轴向力系数、法向力系数和压心位置，然后根据这三个量可计算出子弹的阻力、升力、侧向力和绕三轴的滚转力矩、偏航力矩和俯仰力矩。公式中涉及到查表计算的地方用Matlab/Simulink 提供的Lookup 模块实现，子弹结构参数通过用m 文件定义变量的方式输入，利用Matlab/Simulink 模块提供的大气环境模块实现对音速、雷诺数随高度变化的实时计算。

利用数值仿真方法对不同结构飘带伞在考虑子弹影响的流场仿真，计算不同结构飘带伞的阻力系数Cs，最后根据量纲分析法拟合出飘带伞的阻力系数公式［6］。利用式( 8)、式(9)建立飘带伞气动解算子模块。

式中:Ss=πD2

s /4 为伞帽轴向投影面积;Ds为伞帽直径;L 为弹伞间距;Dd为子弹直径;M 为马赫数;Fs为伞的阻力系数。

图3 弹道解算模块

3 弹道模型验证

利用上述仿真平台对某伞弹系统以初速750 m/s，弹道倾角为-70°，在1 100 m 高空被投放进行计算，得出俯仰角、速度随时间变化曲线，如图4 所示。计算结果为: 子弹下落时间tc=9.3 s，落速vc=60.7 m/s。这与文献［6］中同等条件下的试验结果下落时间tc=8 ～12 s，子弹落速为vc=50 ～80 m/s 相比，属于其结果范围，由此基本验证了所建立的气动弹道仿真平台的可行性和合理性。

图4 某飘带伞子弹稳定段弹道特性参数曲线

4 伞弹系统结构参数对弹道特性影响分析

4.1 问题描述

正交试验就是利用正交表来合理安排试验，并运用数理统计原理分析试验结果、处理多因素试验的科学方法。它能通过代表性很强的少数次试验，摸清各个影响因素对试验指标的影响情况，确定出不同影响因素的主次顺序。本文所选取的试验指标为tc( 下落时间)、vc( 落速)、ϑc( 着地时的俯仰角)和αc( 着地时的攻角)，影响因素为xg/Dd( 子弹质心与弹径之比)、Dst/Dd( 伞帽直径与弹径之比)、Lds/Dd弹伞间距与弹径之比)、λn( 子弹长径比)以及头部形状。用A、B、C、D、E分别表示xg/Dd、Dst/Dd、Lds/Dd以λn及头部形状。每个影响因素选取4 个不同的状态为因素水平，其分别为:

A:1.6、1.8、2.0、2.2;

B:0.6、0.7、0.8、0.9;

C:4、5、6、7;

D:2、2.5、3、3.5;

E:锥形(1)、尖拱形(2)、抛物线形(3)、平头(4)。

4.2 初始条件

子弹初始速度: v0=750 m/s; 子弹初始高度: y0=1 100 m;子弹初始弹道倾角: θ0= -70°; 子弹初始俯仰角: ϑ0=-70°;子弹初始弹道偏角: ψv0=0; 子弹绕x1轴的旋转初始角速度:ωx1=0;子弹绕y1轴的旋转初始角速度: ωy1=0; 子弹绕z1轴的旋转初始角速度:ωz1=0;子弹长径比λ=4.3。

根据试验要求采用L16( 45)类型的正交表，表中每个因素有4 个水平，在不考虑交互作用的情况下可以进行最多包含5 个因素的试验，对各种水平的组合要进行16 次试验。试验安排及结果如表1 所示。

表1 不同影响因素下的正交试验数据

子弹的落角等于落地时的俯仰角和落地时的攻角之差的绝对值，因上述各次试验结果中落地时攻角都远远小于落地时俯仰角，可近似认为落角等于落地时俯仰角。

经过极差分析可得出各因素对指标的影响程度，如表2所示，从中可以看出，影响子弹下落时间、落速、落角的前三个因素均相同，影响程度由大到小依次为:头部形状、伞帽直径和弹伞间距。对攻角的影响主次顺序则依次为伞帽直径、头部形状和弹伞间距。

表2 影响因素对试验指标的极差分析

头部形状对下落时间、落速和落角影响较大，这主要是钝头弹阻力较大引起的。弹伞间距决定了伞帽阻力对子弹质心的力臂，因此会影响伞帽阻力提供的稳定力矩大小。同时考虑了子弹对伞帽周围流场的影响，弹伞间距越小，伞帽越靠近子弹弹底部的涡流区，从而影响伞帽所受到的空气阻力，最终也会影响弹落点性能。

质心位置和头部长径比对所选取的试验指标影响都较小，这是因为伞弹系统中子弹的姿态主要靠伞的作用来稳定，而对子弹质心位置要求较低。对一定头部形状的子弹，头部长径比对子弹气动参数影响较小，从而对伞弹系统弹道特性的影响较小。从16 次仿真试验结果可以看出，柔性飘带和金属伞帽组成的飘带伞对不同结构参数的伞弹系统都能起到很好的稳定作用。

5 结束语

基于伞轴始终沿速度方向的假设建立了柔性飘带与金属伞帽组成的飘带伞弹系统稳定下落段弹道模型。利用Matlab/Simulink 软件建立了该伞弹系统的仿真平台并进行了校验，基于该仿真平台和正交试验对不同结构伞弹系统弹道落点特性进行分析，得出了结构参数影响落速、落角、下落时间的主次关系依次均为: 头部形状、伞帽直径、伞弹间距。本文仅考虑了该飘带伞弹系统在稳定段的弹道特性，子弹从抛撒到稳定之前这段弹道尚需进行深入研究。

［1］杨启仁.子母弹飞行动力学［M］.北京:国防工业出版社，1999.

［2］李国杰，冯顺山，曹红松.超音速伞-弹系统三维有风弹道计算方法研究［J］.弹箭与制导学报，2007，27(5):167 -17.

［3］丛明煜，邵成勋，张家兴，等.低空伞弹外弹道动力学模型［J］.弹道学报，2000，12(1):31 -36.

［4］钱杏芳.导弹飞行力学［M］.北京:北京理工大学出版社，2008.

［5］张志涌. 精通MATLAB6［M］.5 版. 北京: 北京航空航天大学出版社，2003.

［6］冯顺山，董永香.伞弹系统弹道研究［R］. 北京理工大学爆炸科学与技术国家重点实验室毁伤理论与技术课题组，2009.

［7］沈仲书，刘亚飞.弹丸空气动力学［M］.北京:国防工业出版社，1984.