QuickBird 遥感图像校正模型

孙 军，黎 琪，李和睿

( 贵州省毕节学院 建筑工程学院，贵州 毕节 551700)

近年来，伴随SPOT5、IKONOS 和QuickBird 等高空间分辨率遥感图像应用的不断深入和普及，如何经济、高效、高精度地纠正高空间分辨率遥感图像的几何变形，已成为实际工作中急需解决的生产难题。高空间分辨率遥感图像的几何变形，将严重影响以遥感图像为基础的不同地类面积量算、地面样地在遥感图像上的定位、遥感定量估测模型、遥感图像融合、各种规划设计等的精度，遥感图像要有效应用于实际生产，需先纠正其几何变形。

对于分辨率在2.5 m 以下的中低分辨率遥感图像，传统校正方法一般是利用1∶1万或1∶:5万比例尺的地形图，通过地形图量测在遥感影像上易于识别的地面控制点平面坐标，然后借助商用遥感图像处理软件进行校正。随着遥感图像空间分辨率的提高，图像变形受地形起伏和传感器倾斜扫描的影响将增大，采用传统基于地形图量测控制点坐标的方法已无法满足校正精度的需要。为此，需借助差分GPS 定位高精度测定一定数量在遥感影像上能够有效识别的地面控制点坐标，采用适当的纠正模型来校正图像变形。为有效校正图像，尽量减少野外测定地面控制点的工作量，需要研究高空间分辨率遥感图像的变形机理及定量描述模型和几何纠正算法，以便探索适合实际生产应用的校正模型和地面控制点配置方案。本文利用实测地面控制点坐标，对QuickBird遥感图像的变形机理进行了初步研究。

1 遥感图像校正模型

遥感图像校正模型是遥感图像校正的核心，决定着遥感图像校正的成功与失败。遥感图像变形主要是受到地面起伏的影响，正确分析高程造成的遥感图像变形机理，对于遥感图像校正模型的研究，有重要作用。本文基于高程造成的遥感图像变形机理，在一般二次多项式的基础上，提出了本文多项式遥感图像校正模型，并用实验对不同的遥感图像校正模型进行了精度比较。

对卫星遥感图像进行几何校正，可以消除图像上的像元在图像坐标系中的坐标与其在地图投影等参考坐标系中的坐标之间的差异，获得无几何变形的数字纠正影像。由于严格几何校正计算量较大、计算复杂，而且需要卫星轨道和传感器参数，在实际应用中有时无法得到这些数据，因此在遥感图像校正中一般都采用直接线性变换、多项式( 一般多项式，改进多项式)等遥感图像校正模型进行近似几何校正。

在传统的校正模型中，一般多项式由于没有考虑高程对遥感图像造成的影响，因此校正精度较低。直接线性变换与改进多项式在引入高程时，要求抽样点和检验点的距离必须相当接近( 在实验中一般采用K -均值聚类方法提取抽样点)，不能在真正的遥感图像校正中发挥实际作用。

在引入高程时，由于考虑到地球自转，地面曲率，大气折射等对遥感图像变形的影响作用不大，因此只考虑地面起伏对遥感图像造成的影响，如图1 所示。

图1 遥感图像影响分析示意图

由于本文实验用的QuickBird 遥感图像为线阵CCD 逐行扫描图像，所以这里只考虑行的情况，列的情况与此相同。在图1 中，D 为遥感图像的中心位置。遥感像片上的点F 所对应的地面位置在B 处，由于受到地形起伏的影响，实际上的位置在A 点的投影点C 处。如果能够把大地坐标的C 点移动到B 点，再利用一般多项式进行校正，就可以得到实用的遥感图像校正模型。

在图1 中，令D 点处的图像行列号为u0，v0，对应的大地坐标为X0，Y0，A 点处的图像行列号为u，v，相应的大地坐标及高程为X，Y，Z。由于△ABC ～△EFD，所以|AC| =Z，|FD| =u-u0，|DE| =h，这里的h 为像片到凸透镜的距离，这样就得到再考虑一般多项式，得到新的遥感图像校正模型为

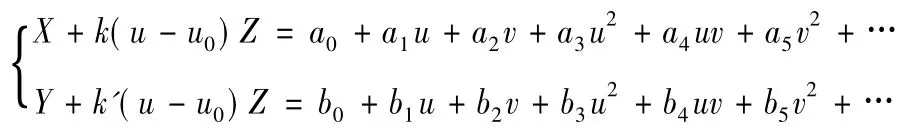
这里的k，k'为相关系数，整理后得到本文遥感图像校正的多项式

其中，u，v 为失真遥感图像的行列号，X，Y，Z 为相应的行列号所对应的地面大地三维坐标( Z 为高程)，其余为相关系数。

2 实验和证明

本文实验用QuickBird 遥感图像研究区域位于深圳市区，所采用的遥感信息源是空间分辨率为0.6m 的QuickBird Pan 波段遥感图像，试验区遥感图像总行列数为26574 ×28606，对应的实地范围为15.944 km ×17.164 km。因深圳已建成GPS 虚拟参考网络定位系统，可以厘米级精度测定地面控制点三维坐标，采用市区的高空间分辨率遥感图像，可有效保证采集一定数量的地面控制点，以便进行研究分析。实验材料来自于西安科技大学测绘学院李崇贵教授研究的国家自然科学基金资助项目(30872023)。

在实验中，先从65 个控制点中提取一部分做为抽样点，其余控制点作为检验点。再用抽样点计算出遥感图像校正模型的系数，得到遥感图像校正模型。然后在模型中代入检验点的失真图像行列号，计算出大地坐标。最后把计算出的大地坐标与实际大地坐标相减，所得的差值的绝对值，就是精度( 也叫误差)。

精度分为拟合精度和检验精度两种，拟合精度就是把已经计算出的校正模型代入抽样点的失真图像行列号，计算出大地坐标，再与实际大地坐标相减，所得差值的绝对值，就是拟合精度。检验精度就是把已经计算出的校正模型代入检验点的失真图像行列号，计算出大地坐标，再与实际大地坐标相减，所得差值的绝对值，就是检验精度。

本文先用K-均值聚类法把65 个控制点聚成30 类，取每个类的接近中心点为抽样点，其余点为检验点，所得的各种精度如表1 所示。

然后再用随机抽取的方法提取30 个抽样点，其余点作为检验点，所得的各种精度如表2 所示。

实验表明，在使用K -均值聚类提取抽样点的情况下，本文二次多项式校正模型的检验精度明显优于其它各种多项式校正模型。在随机抽取抽样点的情况下，本文二次多项式校正模型的拟合精度明显优于其它各种多项式校正模型，检验精度优于改进二次多项式。

表1 K-均值聚类抽样检验精度表

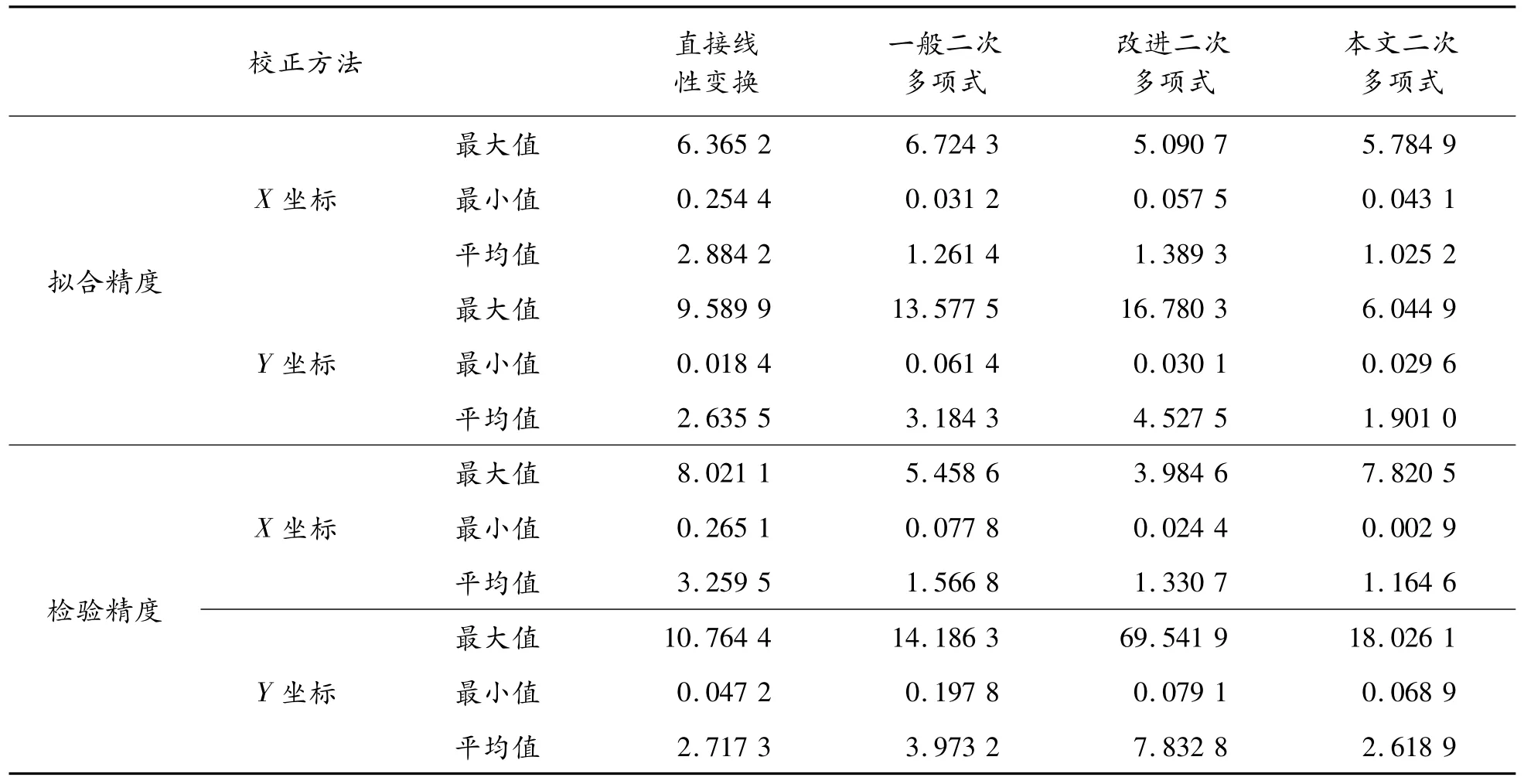
表2 随机抽样检验精度表

3 结束语

QuickBird Pan 波段遥感图像变形主要受地形起伏的影响，地形起伏变化越大，图像变形也就越大。图像变形受地形起伏、倾斜扫描、传感器姿态角变化等诸多因素的影响，很难对每个因素的影响进行定量表达。控制点的数量和分布，对主要影响因子的筛选有一定影响，但当尽可能考虑多的影响时，所建模型就能取得良好的效果。在遥感图像校正中，高程的引入可以让遥感图像的校正变得更加精确。由于在实际应用中能够用于计算遥感图像校正模型的控制点数量稀少，使得大量的像素点都远离已知控制点，因此在实际应用中多项式的校正效果要比改进多项式好得多。

［1］A Goshtasby.Piecewise linear mapping functions for image registration［J］. Pattern Recognition，1986，19 ( 6): 459-466.

［2］Smith M，Park G. Absolute and exterior orientation using linear features［J］. International Archives of Photogrammetry and Remote sensing，2003，28(5):505-509.

［3］J A Noble.Finding corners［J］. Image Computing，1988，6(2):121-128.

［4］J S Lee，Y N Sun，C H Chen，C T Tsai.Wavelet based corner detection［J］. Pattem Recognition，1993，26( 6): 853-865.

［5］章孝灿，黄智才，赵元洪.遥感数字图像处理［M］.杭州:浙江大学出版社，1997.

［6］朱述龙，张占睦.遥感图像获取与分析［M］.北京:科学出版社，2000.

［7］徐青，张艳.遥感影像融合与分辨率增强技术［M］.北京:科学出版社，2007.

［10］孙家抦. 遥感原理与应用［M］. 武汉: 武汉大学出版社，2006.

［11］陈建胜.少控制点的推扫式卫星姿态参数外推方法研究［J］.中国图像图形学报，2009，8(8):1469-1474.

［12］张翼.获取均匀控制点的遥感影像自动空间匹配方法［J］.中国图像图形学报，2009，8(8):1475-1479.