呼吸道传染病空气传播的感染概率的预测模型

钱 华 郑晓红 张学军

(1东南大学能源与环境学院，南京210096)

(2浙江大学制冷与低温研究所，杭州310027)

自2003年SARS爆发之后，室内空气环境安全的重要性得到越来越多的认同.尽管SARS已经过去，但通过散发炭疽或天花病毒等引发的生物恐怖［1］以及可能到来的禽流感爆发依然威胁人类［2］.而且，根据世界卫生组织的报告，每年由于肺结核这种空气传染病而死亡的人数就达到了170万［3］.随着城市化水平的提高，现代大型城市日趋拥挤的居住环境和高速增长的世界范围的运输网络都会加速造成空气传播疾病的传播过程，这种特点在2003年SARS流行中已经得到发现［4-5］.

很多研究表明空气传染病与通风量、气流组织等因素相关［4］，而认识空气传染病的传播途径，以及准确预测空气传染病的感染概率及其影响因素有助于采取措施降低感染概率.因此，本文回顾了空气传染病的传染途径及其特点，以及空气传染病的感染概率预测方程.

1 空气传播疾病的传播特点

空气传染病的历史非常悠久.在公元一万年前，非洲东北部就爆发过天花流行病［6］.由于空气传染病的传播途径不够清晰，所以在古代西方社会，人们认为巫术和恶毒的巫婆是空气传染病的罪魁祸首.最早“科学”地阐述空气传染病传播的理论出现在16世纪［7-8］，该理论认为空气传染病是由空气中的瘴气(miasmas)和坏的空气(malaria)导致［8］.然而，细菌理论诞生后，普遍认为空气传染病只能依靠接触和飞沫传播［8］.1934年，Wells假设飞沫核是空气传染疾病传播途径［9］，并且实验验证了该机理［10］，之后，才建立起科学的空气传染病的传播途径理论.

当一个病人在进行呼吸、说话、唱歌、咳嗽和打喷嚏等活动时，会排出含有病原体的飞沫.Wells通过计算发现，在室内环境中，小于100 μm的飞沫能够快速蒸发，并在6 s内干燥成飞沫核［9］.这些飞沫核会含附在原先就在飞沫中且没有在干燥和脱水过程中死亡的病原体上.这些含有病原体的飞沫核如果被健康人员吸进体内，可能会导致传染病的发生.研究表明，咳嗽导致的飞沫核大部分集中在2.1～3.3 μm，绝大多数飞沫核小于 5 μm［11］.大颗粒物被吸进人体时，会被鼻腔或上呼吸道黏住，细微颗粒物的惯性比较小，很容易进入人的下呼吸道直至肺部底层［12］.图1给出了不同粒径颗粒物被鼻腔、上呼吸道和下呼吸道吸收的比例分布，可看出小于3 μm的颗粒大部分能进入到人的下呼吸道.Ratcliffe和Wells于1948年做了一个实验，把2组兔子分别暴露于含有肺结核菌粒径为2 ～3 μm 和12 μm 的颗粒中［10］.结果表明，暴露于2～3 μm含肺结核菌颗粒中的兔子几乎全部感染上肺结核，而暴露于12 μm含肺结核菌颗粒中的兔子只有6%感染上肺结核，从而进一步证明了细微颗粒即飞沫核小的颗粒是导致空气传播疾病病原体的载体.由Stokes计算式可以得出，2～3 μm颗粒的沉降速度大约在0.15 mm/s.较低的沉降速度使得颗粒物几乎悬浮在空气中，并随着气流散布在空间中.

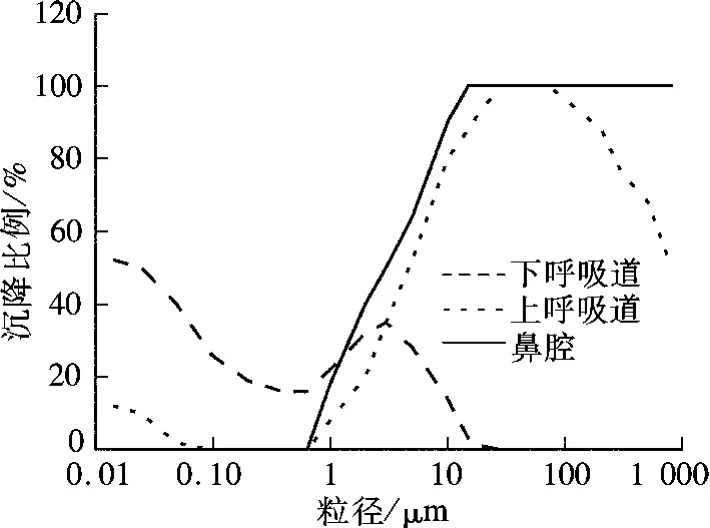
图1 不同粒径颗粒物在呼吸道中的沉降比例［13］

2 空气传播疾病感染概率预测方法

感染概率与很多因素有关，如病原体的数量、病原体的种类、传播途径以及宿主的易感性等［12］.由于这些参数很难完全精确确定，因此导致无法精确确定空气传染病的感染概率.Wells在1955年发展了一个概念“quanta”，利用这个概率发展方法从而确定空气传染病的感染概率［14］.quanta定义为使一个人达到致病量的最少病原体的数目，这是一个统计意义上的概念.因此，Wells指出，吸入一个quanta量的人平均感染概率服从Poisson分布，也就是有63.2%(即1－e－1)的概率会感染上空气传染病.

根据这个理论，Riley等根据古典的传染病感染概率预测方程发展了空气途径传染病概率方程［12］.

2.1 MA模型

MA(mass action)模型为

式中，r为有效接触率;C为一次爆发中新产生的被感染人数;I为感染人数;S为总的易感人数.式(1)可用来预测一次爆发中传染病感染概率.

基于上述理论，病原体附在飞沫核上并散布在空气中.如果假设飞沫核是均匀散布于整个空间，就可以算得一个人在空气中呼吸所得的quanta值，从而计算出有效接触率(即一个人所吸入的quanta数)，即

式中，q为一个感染者的quanta产生率;p为呼吸通风量(m3/h);Q为房间的通风量(m3/h);t为暴露时间(h).

把式(2)代入式(1)，可以得出感染概率为

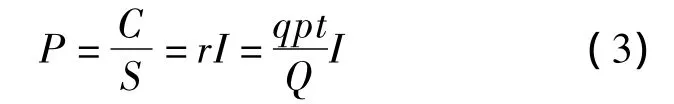
式(3)没有考虑不同的平均感染概率，如果quanta值很高，计算出的感染概率可能会超过1，这显然过高.所以，Riley等在1978年根据Wells的理论发展了Wells-Riley方程，且成功地验证和预测了美国纽约州罗切斯顿附近一所郊区小学的麻疹爆发情况［15］.

2.2 Wells-Riley模型

Wells-Riley模型为

Wells-Riley模型基于上文提到的Wells假设，认为平均概率服从 Poisson分布，由Riley等于1978年提出［15］.该模型基于以下假设:

1)飞沫核均匀散布在整个空间的空气中，也就是说空气在房间中是充分混合的，房间各处的浓度相等，即房间内任何一处被感染的概率相等.

2)飞沫核的浓度在整个感染时间内是稳定的，即感染者呼出的病原体量(quanta值)、感染者的数量、通风量等在整个感染时间内是稳定的.

3)忽略生物病毒在被通风带出病房前的死亡率.

4)忽略通过泄漏、过滤或沉降等方法移出房间空气中的飞沫核数.

Wells-Riley模型除了成功地预测了美国那所郊区小学的麻疹爆发情况外，该方程及其改进方程也被广泛用来预测各个空气传染疾病的爆发情况［11，16-25］，甚至用来评估请病假和通风系统之间的关系［19］.

2.3 Wells-Riley模型的发展

Wells-Riley模型的发展基本上是围绕着Wells-Riley方程的假设条件来改进的，使得预测的感染概率更加符合实际情况，有些甚至用来检验除菌设备的效果.

Seppanen等于2006年考虑了空气过滤器和颗粒沉降效果，发展了Wells-Riley方程，得到如下形式［19］:

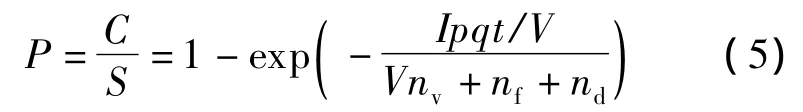
式中，V为房间体积(m3);nv为换气次数，nv=Q/V(次/h);nf为回风量和过滤器过滤效率的乘积;nd为飞沫核沉降在室内表面上的数量.

Fennelly等［18］在考虑了口罩等的作用后，将Wells-Riley模型发展为

式中，θ(取值范围为0～1)为口罩的渗透系数.θ=1时，表示飞沫核能够完全渗透到人的呼吸区，没有口罩或者口罩完全不起作用.

Rudnick等［24］发展了 Wells-Riley方程，用于预测非稳定状态下(如通风量变化的情况下)的感染概率，利用CO2浓度作为呼出气体暴露的指标.当一个房间内部没有其他CO2源时，CO2浓度能够反映人的呼吸和通风情况.该模型适合预测非稳定和通风系统性能不好情况下的感染概率分布，即

式中，Ca为人呼出气体中CO2的体积分数;Ve为呼出气体在房间内的等价体积;Cin和Co为室内和室外的CO2体积分数.

Qian等［26］把 Wells-Riley方程和 CFD 相结合，发展了如下模型:

式中，N为quanta的浓度 (quanta/m3);V和Vs分别为速度矢量和颗粒物的沉降速度矢量，Vs可根据颗粒物的密度和尺寸由Stokes方程求得;ρ为空气密度;Γ为飞沫核的扩散系数.

根据方程(9)计算得到的quanta的浓度，求得房间内易感人群总的概率为

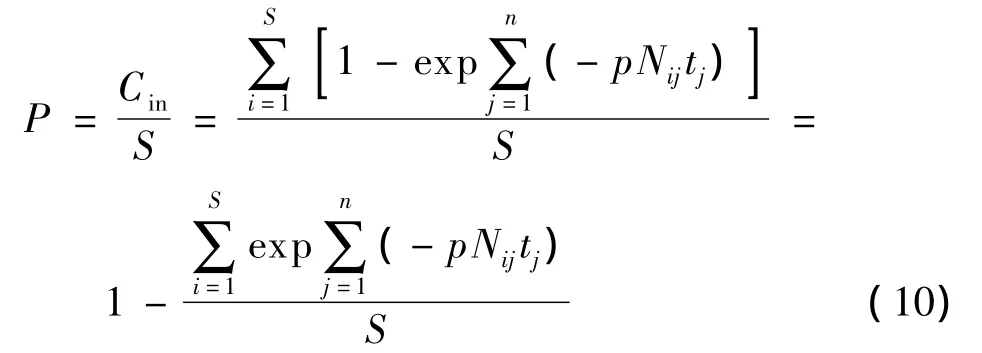
式(10)能够用来预测室内气流组织对感染概率的影响，有助于改进通风系统以降低呼吸道传染病的感染概率.

3 讨论

3.1 quanta值对感染概率的影响

不同的疾病和不同的感染者所产生的quanta值是不同的.当感染者所呼出的病原体特别多、quanta值特别大时，感染者容易感染他人，从而引起疾病暴发，这样的感染者被称为超级传播者(super spreader).从图2可以看出，换气次数达到10次/h的情况下，100 quanta/h的quanta产生率所导致的感染概率低于1%，而1.2×104quanta/h的quanta产生率所导致的感染概率接近100%.所以对不同的quanta产生率的病人，采取的控制措施也不同.表1列出了不同疾病的平均quanta产生率和世界上几次爆发大规模传染病例中的quanta产生率.由表可见，肺结核的平均quanta产生率仅为1.25 quanta/h，而最高的肺结核爆发达到惊人的3.084×104quanta/h.此时仅靠通风难以解决交叉感染问题，应该采取隔离病房、戴口罩和穿防护服等方法避免交叉感染.

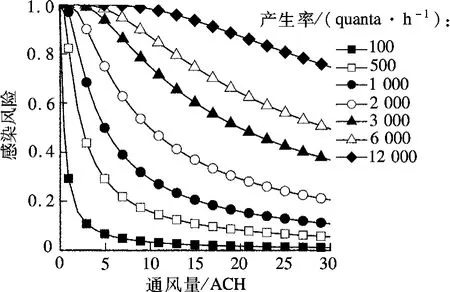
图2 感染风险随quanta产生率及通风量变化的关系［27］

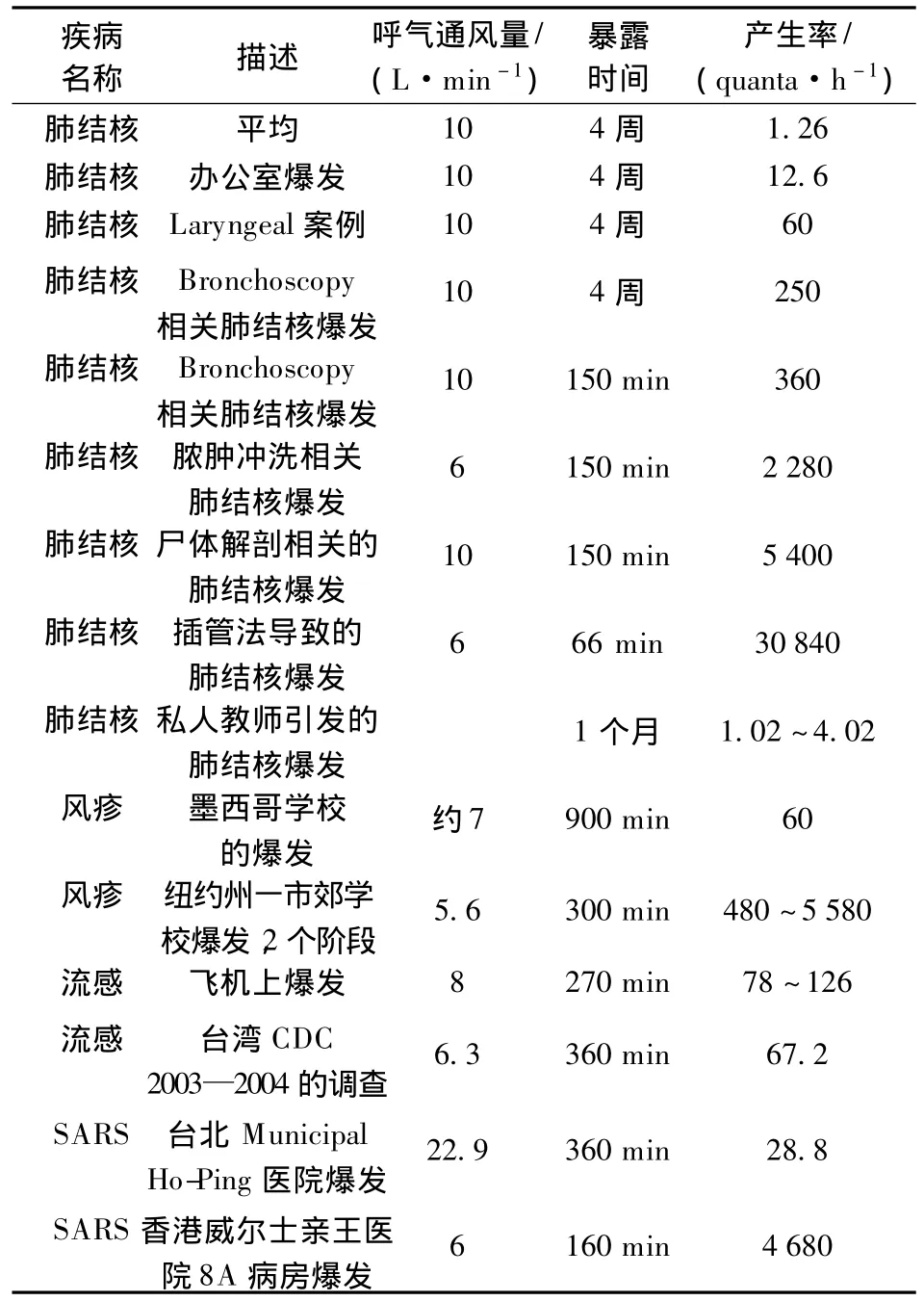
表1 肺结核、麻疹、流感及SARS的quanta产生率［13］

3.2 通风量对感染概率的影响

从图2和表1可以看出，除特别极端的案例，通风都能够有效降低感染率，但是加大通风同样会带来能耗、管道设计和过滤器造成的压降以及风机功率等各方面的难题.虽然没有明显的证据显示确定的通风量能够平衡各方面因素而达到最优［4］，但各个国家在新的隔离病房标准或指南中对新风的最低换气次数要求依然比较高，达到12次/h［28］.大的通风量不仅能够快速稀释感染者所呼出的飞沫核从而降低感染率，而且能够快速移除室内污染物使得室内污染物浓度能够快速下降.

如果通风量不足，可以通过加入室内净化器的方法来提高等效通风量，如方程(5)所示.香港特区政府在SARS之后，建立了大量高标准的隔离病房，但是隔离病房由于造价和维护成本较高，不可能普及到所有病房.如果遇到禽流感爆发而导致隔离病房病床数不够时，可利用室内净化器、加装风扇等方法使得普通病房成为隔离病房.

3.3 其他风险预测模型

在预测呼吸道传染病的模型中，除了Well-Riley模型外，Dose-response模型的应用也非常广泛.Dose-response模型最早用于计算有害化学物质对健康的风险和影响，后来发展到用来计算水媒传染和食物传染风险［29］.之后又被推广用来计算空媒传染疾病［30］.但应用Dose-response模型要求确定病原体的剂量以及能够致病的剂量，而呼吸道传染病的爆发案例多数是通过事后研究来获取原因及因素，事后很难确定病原体的剂量，这就限制了Dose-response的应用;而且早期Dose-response模型不能用来预测感染风险的空间分布.Sze-To在Dose-Response模型上做了很多工作用，以预测呼吸道疾病的风险［31］.

4 结语

回顾了空气传染病的特点、感染概率的计算公式以及quanta的产生率，并利用这些公式考察了quanta产生率和通风对感染概率的影响.分析结果显示，对绝大部分传染病，通风可以有效降低感染概率，但对于一些超级传播者所产生的极端高的quanta产生率，仅凭借通风难以有效降低感染概率.因此采用个人护具如口罩、防护服、手套等就可能成了重要和必不可少的降低感染概率的方法.

References)

［1］Gonzalez J C.Bio-terrorism，"dirty bombs，"hospitals，and security issues［J］.J Healthc Prot Manage，2004，20(2):55-59.

［2］Gruber P C，Gomersall C D，Joynt G M.Avian influenza(H5N1):implications for intensive care［J］.Intensive Care Medicine，2006，32(6):823-829.

［3］World Health Organization.WHO report 2006 global tuberculosis control:surveillance，planning，financing［R］.Geneva:WHO，1970.

［4］Li Y，Leung G M，Tang J W，et al.Role of ventilation in airborne transmission of infectious agents in the built environment—a multidisciplinary systematic review［J］.Indoor Air，2007，17(1):2-18.

［5］Allenby B，Fink J.Toward inherently secure and resilientsocieties［J］. Science， 2005，309(5737):1034-1036.

［6］Snodgrass M E.World epidemics:a cultural chronology of disease from prehistory to the era of SARS［M］.London:McFarland ＆ Company，2003.

［7］Ayliffe G A J，English M M P.Hospital infection:from miasmas to MRSA［M］.Cambridge，England:Cambridge University Press，2003:274.

［8］Langmuir A D.Airborne infection:how important for public health?Ⅰ.a historical review［J］.Am J Public Health Nations Health，1964，54(10):1666-1668.

［9］Wells W F.On airborne infection studyⅡ.droplets and droplet nuclei［J］.American Journal of Hygiene，1934，20(3):619-627.

［10］Ratcliffe H L，Wells W F.Tuberculosis of rabbits induced by droplet nuclei infection:Ⅰ.initial response to infection［J］.Journal of Experimental Medicine，1948，87(6):575-584.

［11］Fennelly K P，Martyny J W，Fulton K E，et al.Cough-generated aerosols of mycobacterium tuberculosis:a new method to study infectiousness［J］.Am J Respir Crit Care Med，2004，169(5):604-609.

［12］Riley R L，O'Grady F.Airborne infection:transmission and control［M］.New York:The Macmillan Company，1961.

［13］Qian H.Ventilation for airborne infection in hospital environment［D］.Hong Kong:Department of Mechanical Engineering of University of Hong Kong，2007.

［14］Wells W F.Airborne contagion and air hygiene:an ecological study of droplet infection［M］.Cambridge，MA，USA:Harvard University Press，1955.

［15］Riley E C，Murphy G，Riley R L.Airborne spread of measles in a suburban elementary school［J］.Am J Epidemio，1978，107(5):421-432.

［16］Beggs C B，Noakes C J，Sleigh P A，et al.The transmission of tuberculosis in confined spaces:an analytical review of alternative epidemiological models［J］.International Journal of Tuberculosis and Lung Disease，2003，7(11):1015-1026.

［17］Brickner P W，Vincent R L，First M，et al.The application of ultraviolet germicidal irradiation to control transmission of airborne disease:bioterrorism countermeasure［J］.Public Health Rep，2003，118(2):99-114.

［18］Fennelly K P，Nardell E A.The relative efficacy of respirators and room ventilation in preventing occupational tuberculosis［J］.Infect Control Hosp Epidemiol，1998，19(10):754-749.

［19］Seppanen O，Fisk W J，Lei Q H.Ventilation and performance in office work［J］.Indoor Air，2006，16(1):28-36.

［20］Gammaitoni L，Nucci M C.Using a mathematical model to evaluate the efficacy of TB control measures［J］.Emerg Infect Dis，1997，3(3):335-342.

［21］Ko G，Thompson K M，Nardell E A.Estimation of tuberculosis risk on a commercial airliner［J］.Risk Anal，2004，24(2):379-388.

［22］Nicas M.Refining a risk model for occupational tuberculosis transmission［J］.Am Ind Hyg Assoc J，1996，57(1):16-22.

［23］Nicas M.Regulating the risk of tuberculosis transmission among health care workers［J］.Am Ind Hyg Assoc J，2000，61(3):334-339.

［24］Rudnick S N，Milton D K.Risk of indoor airborne infection transmission estimated from carbon dioxide concentration［J］.Indoor Air，2003，13(3):237-245.

［25］Seppanen O A，Fisk W J.Summary of human responses to ventilation［J］.Indoor Air，2004，14(sup 7):102-118.

［26］Qian H，Li Y，Nielsen P V，et al.Spatial distribution of infection risk of SARS transmission in a hospital ward［J］.Building and Environment，2009，44(8):1651-1658.

［27］Qian H，Li Y G，Seto W H，et al.Natural ventilation for reducing airborne infection in hospitals［J］.Building and Environment，2010，45(3):559-565.

［28］Wang J，Qian H，Zhang X.Influence of environmental conditions on airborne infection risk in ward［J］.Journal of Southeast University:English Edition，2010，26(2):266-269.

［29］Haas C N.Estimation of risk due to low doses of microorganisms:a comparison of alternative methodologies［J］.Am J Eidemiol，1983，118(4):573-582.

［30］Armstrong T W，Haas C N.A quantitative microbial risk assessment model for legionnairs's disease:animal model selection and dose-response modelling［J］.Risk Anal，2007，27(6):1581-1596.

［31］Sze-To G N，Chao C Y H.Review and comparison between the Wells-Riley and dose-response approaches to risk assessment of infectious respiratory diseases［J］.Indoor Air，2010，20(1):2-16.