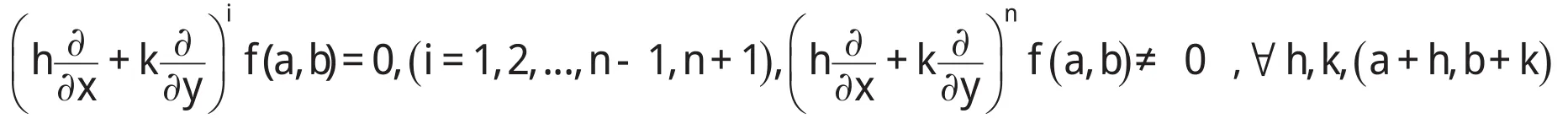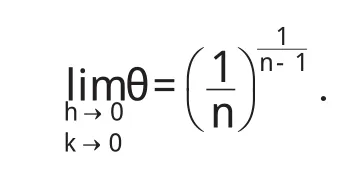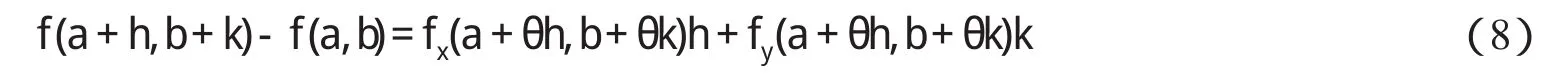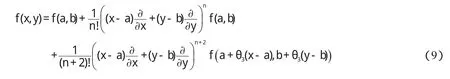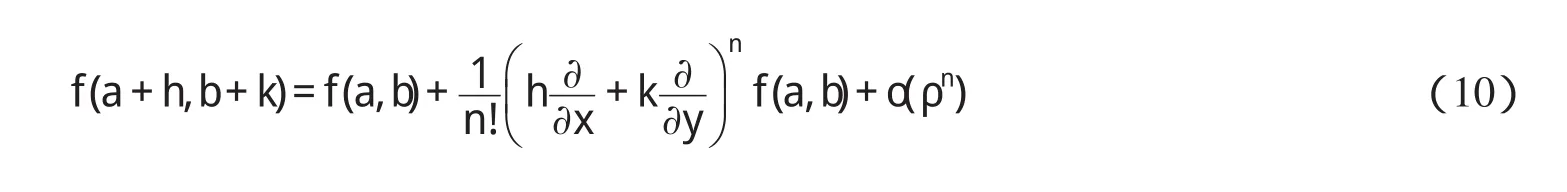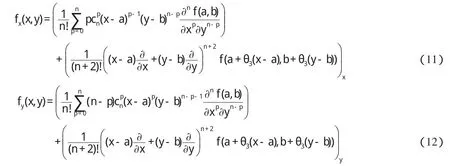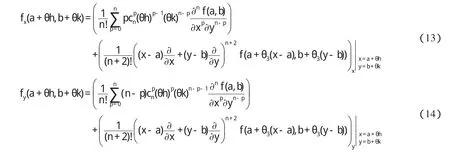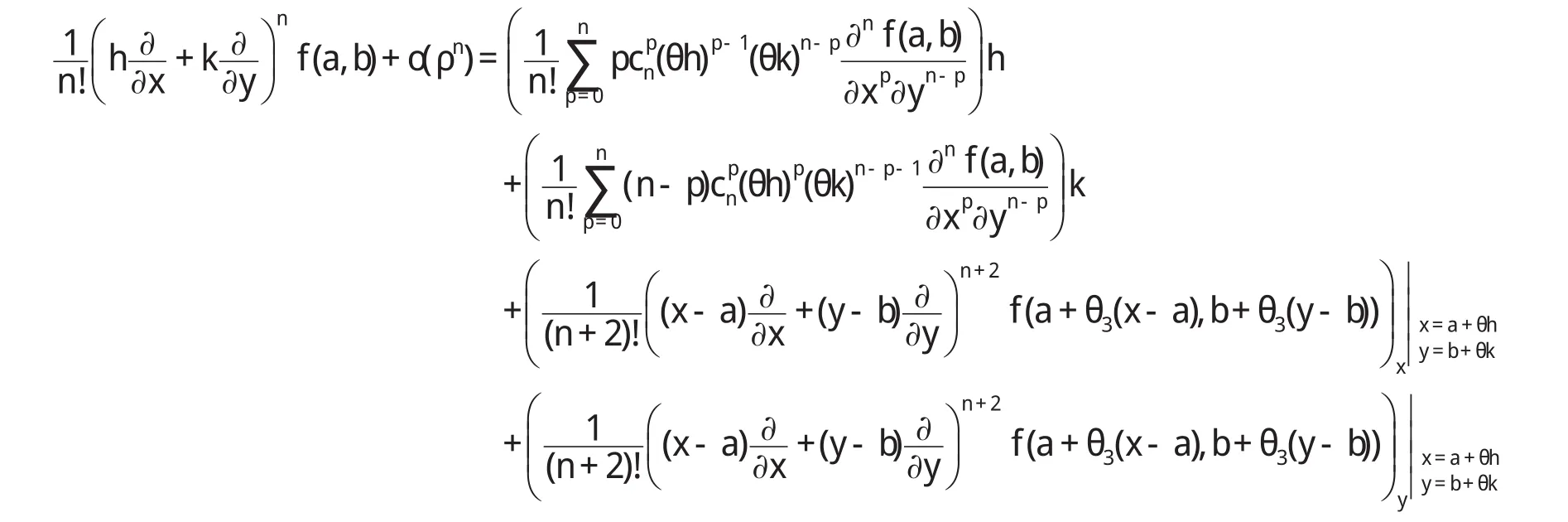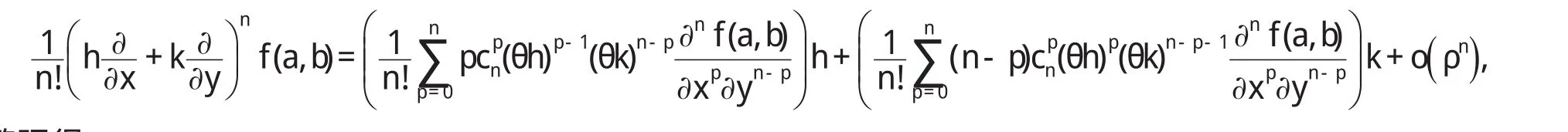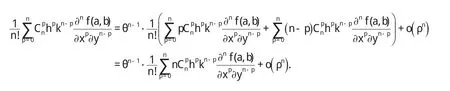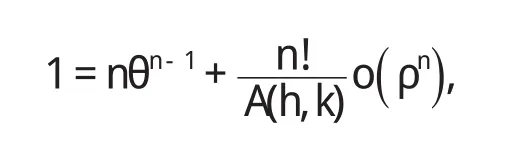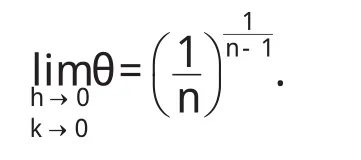微分中值定理中值点的渐近分析

王申秋，凡震彬

（常熟理工学院 数学与统计学院，江苏 常熟 215500）

1 引言

中值定理是微积分学课程的基本定理之一[1-2]，其在整个微积分课程体系中起到非常重要的作用．在许多的微积分学教材中对此都有详细的描述，但这些教材都只说明了中值点的存在性，而没有涉及中值点的其他性质，特别是渐近性质．

1982年，Alfonso G.Azpeitia[3]发表了一篇重要的文章，首次讨论了Lagrange中值定理中的中值点的如下渐近性质．

定理 设函数 f在闭区间[a,x]上二阶可导，f''在点a点处右连续且 f''(a)≠0，则Lagrange中值定理中的中值点ξ满足：

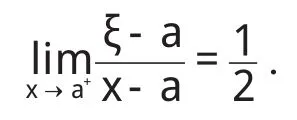
随后这一结论被不断推广，并在各种实际问题中得到应用，尤其是在各种问题的近似求解中得到广泛应用，并取得了令人满意的结果．

2009年12月，程希旺[4]发表了《二元函数微分中值定理中值点的分析性质》这一文章，其主要讨论了二元函数Lagrange微分中值定理中值点的连续性及可导性问题，并给出了二元函数Lagrange微分中值定理中值点连续及偏导数存在的充分条件，同时给出了计算其偏导数的公式．

2010年1月，时玉敏[5]发表了题为《微分中值定理中ξ的渐近性质》的文章，文中主要给出了一元函数Cauchy中值定理中值点的渐近性质．

本文主要利用微分中值定理和泰勒公式继续研究上述问题，给出了一元函数Cauchy中值定理以及二元函数微分中值定理中值点渐近性质的新的充分条件．

2 主要结果

首先我们将一元函数Cauchy中值定理以及二元微分函数中值定理引述如下：

Cauchy中值定理：若函数 f (x)及g(x)在闭区间[a , b ]上连续，在开区间(a , b )内可导，f'(x)与g'(x)不同时为零，并且g(a)≠g(b)，则在开区间(a , b )内至少存在一点ξ，使下式成立：

二元函数中值定理：设二元函数 f 在凸开域D⊂R2内可微，(a,b)∈D，则对任意的(a+h,b+k)∈D，有

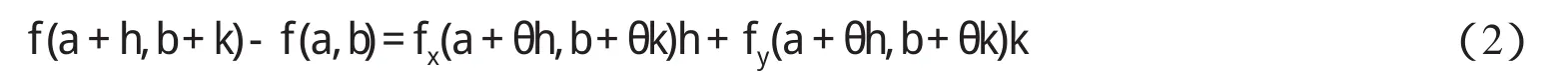
其中0<θ<1.

下面，我们给出上述中值定理中中值点ξ和θ的渐近分析结论．

定理1 设Cauchy中值定理中的函数 f (x)，g(x)满足

（I）f(x),g(x)在闭区间[a , b ]上分别具有直到n+2，m+2阶连续导数，其中n,m均是自然数，且n≠m；

（II）f(i)(a)=0(i = 1,2,3,...,n-1),f(n)(a)≠0，g(j)(a)=0( j = 1,2,3,...,m-1),g(m)(a)≠0；

（III）ϕ(x)在区间[a , b ]上连续可微，且 ϕ'(a)≠0．

则柯西中值定理中的ξ满足：

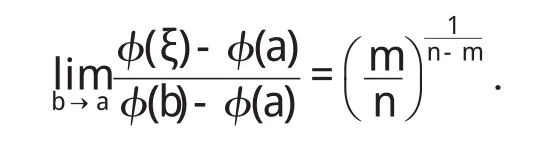
证明 根据条件（I）（II）以及Taylor公式有：

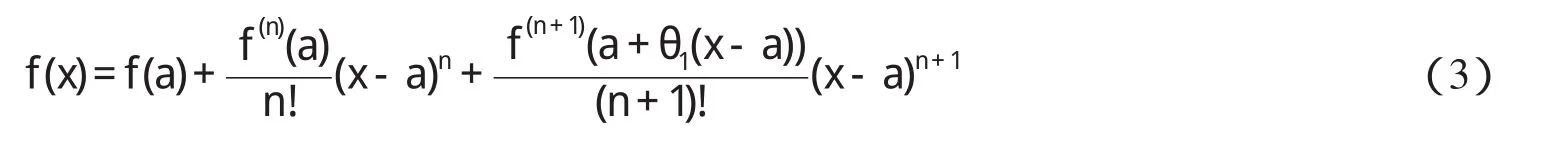
其中0<θ1<1，x∈[a,b].同时，我们有

对（3）式求导，得

特别地，

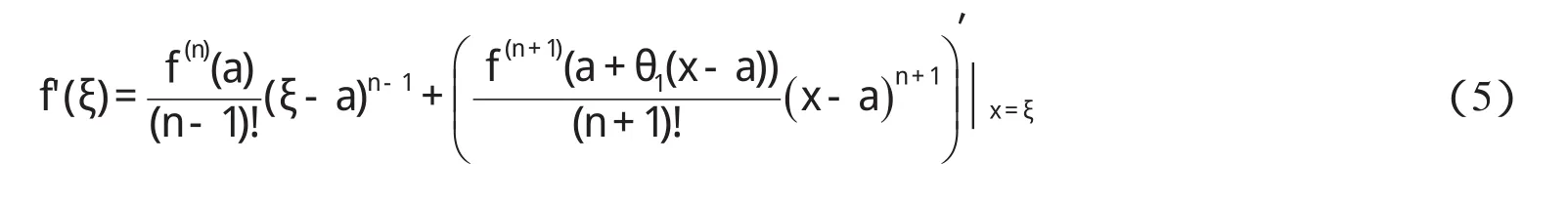
同理，

其中0<θ2<1.

注意到，由条件（I）以及无穷小量的性质，有

在（1）式两边同时乘以(b-a)m-n，即有

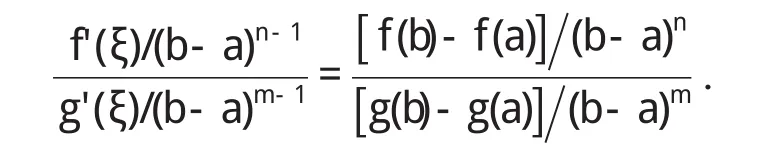
再将（4）-（7）代入上式,并在等式两边同时取极限b→a，可得

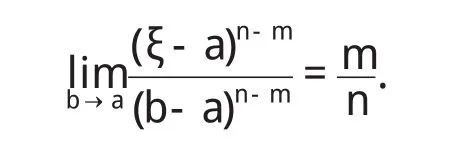
故，由条件（III）存在 a<η1<ξ,a<η2

注1：在定理1中，我们只需要函数 f,g分别具有直到n+2,m+2阶连续导数，这减弱了函数 f,g分别具有直到n+3,m+3阶连续导数并且具有单调性这些要求[4-9]．

定理2 二元函数微分中值定理中的函数 f满足：

（I）f(x,y)在凸开域D⊂R2内具有直到n+3阶连续偏导数，其中n≥2；

（II）∈D.

则二元函数微分中值定理中的θ满足：

证明 根据二元函数微分中值定理，有

其中0<θ<1.

又由二元函数Taylor公式及条件（I）（II），对任意的( )

x,y∈D,存在0<θ3<1，使得

并且

对（9）式求偏导数，得

令 x=a+ θh,y=b+ θk,分别代入（11）（12）式，得

再将（10）（13）（14）代入（8），得

注意到上式右端最后两项也都是ρn的高阶无穷小，故我们有

整理得

从而

定理2给出了一个新的渐近分析结论．

[1]华东师范大学数学系.数学分析（上）[M].北京：高等教育出版社，2006.

[2]华东师范大学数学系.数学分析（下）[M].北京：高等教育出版社，2007.

[3] Alfonso G, Azpeitia. On the Lagrange remainder of the Taylor formula[J]. Amer Math Monthly, 1982, 89: 311-312.

[4]程希旺.二元函数微分中值定理中值点的分析性质[J].数学理论与应用，2009，29（4）：104-107.

[5]时玉敏.微分中值定理中 ξ的渐近性质[J].河南科学，2010，28（1）：15-17.

[6]程希旺.微分中值定理中值点渐进性研究的新进展[J].数学的实践与认识，2009，39（14）:229-231.

[7]任立顺，高继梅.关于复函数高阶微分“中值点”的渐近性[J].大学数学，2007，23（3）：144-148.

[8]郑权.中值定理“中间点”的渐近性质[J].数学的实践与认识，198 5，15（2）：53-57.

[9]张毅，白波，梁坚.广义微分中值定理“中间点”ξ的单调性连续性和可导性[J].大学数学，2010，26（2）：8 9-92.