粗糙认知图RCM模型研究

张春英，刘璐，欧阳东

(1.河北联合大学 理学院，河北唐山 063009;2.河北联合大学轻工学院，河北唐山 063009)

0 引言

认知图(cognitive map，CM)［1］是表示和推理系统中概念间因果关系的图模型。Kosko在1986年在Axelord认知图概念间的因果关系中引入模糊测度，提出了模糊认知图(fuzzy cognitive map，FCM)［3］，用于概念间模糊因果关系的表达与推理。我国学者骆祥峰［5］在2003年首次在概念间的因果关系中引入条件概率测度，提出概率模糊认知图模型，该模型具有简单、鲁棒性好、实用等特点，具有比FCM模型对现实世界更为真实的模拟能力。然而，模糊认知图和概率模糊认知图仅从单个方面考虑，认为概念间的关系是唯一的，并且常常用一个固定的由专家主观确定的模糊测度来反映。但是现实中，两概念间的关系往往是多种多样的，并且具有相应的属性，因此用以表示概念间关系的边会有多条，每条边具有不尽相同的属性权值，且权值随着时间的变化、事件的发展而不断变化。而在分析问题时，这些概念间的关系类的划分是随着人们的认识能力及具体要求的改变而改变的，这就涉及知识的分类及问题的表示，属于不确定性问题中的粗糙问题。故此，本文将粗糙集［6］的思想融入到认知图中，提出粗糙认知图(Rough Cognitive Map，RCM)模型，粗糙认知图可以将认知图当中边粗糙问题合理的转化并解决，抽象出两概念间的一个综合关系，赋予权值，以完成认知图的关系推理过程，并进行应用研究。

1 基本概念

1.1 认知图及模糊认知图

认知图是一种以图形的描述形式表示复杂系统模型的因果关系的方法。它用节点和边分别表示概念(concept)及概念间的因果关系(relations of concept)，是表示和推理系统中概念间因果关系的图模型。

认知图的定义为:

定义 一个基本CM的拓扑结构是一个三元序组U=(V，E，W)，其中V={v1，v2，...vn}表示CM的概念节点集合，E={＜vi，vj＞|vi，vj∈V}是所有节点间的因果关联有向弧。有向弧＜vi，vj＞表示节点vi对vj有因果关联或影响)，W={wij|wij是有向弧＜vi，vj＞的权值}(即wij表示结点ci对cj的关联或影响强度)。每个节点有一个状态空间，(t)表示节点ci在t时刻的状态值，(t)∈［－1，1］，其状态值越大表示该概念的状态越活跃。节点间有向连接弧对应的权值wij∈－1，0，{ }1 ，表示概念间关系增加与减少两种定性状态。

模糊认知图［3，4，7］把概念间的三值{－1，0，1}逻辑关系扩展为区间［－1，1］上的模糊关系。其概念值为模糊值，也可以为二值，反映该节点对某概念以某种程度发生或表示概念状态是关还是开。概念间的因果关系是模糊关系，其联系强度也为模糊值。概念节点的输出与两种类型水平有关，即概念节点自身的状态水平与外部因果联系的强度。通过整个网络中各概念节点的相互作用来模拟系统行为，是一种无监督模型(unsupervised models)。

FCM推理的数学模型为:

式中Vci(t)为原因概念结点ci在t时刻的状态值，Vcj(t)为结果概念结点cj在t+1时刻的状态值，w为与cj有邻接关系的概念结点集合，f为阈值函数(threshold function)，可以是二值的、S型的、模糊集合或概率函数。

1.2 粗糙集理论

设U是非空有限论域，R是U上的二元等价关系，R称不可分辨关系，序对A=U，()R称为近似空间。U/R是U上由R生成的等价类全体，它构成了U的一个划分。U上的一族划分称为关于U的一个知识库(knowledge base).令X⊆U，R为U上的一个等价关系。当X能表达成某些R基本范畴的并时，称X是R可定义的，否则，称X是R不可定义的。R可定义集也称为R精确集，而R不可定义集称为R粗糙集［6］(Rough Set)。

令知识库K=U，()R，集合X⊆U，R是一个等价关系:

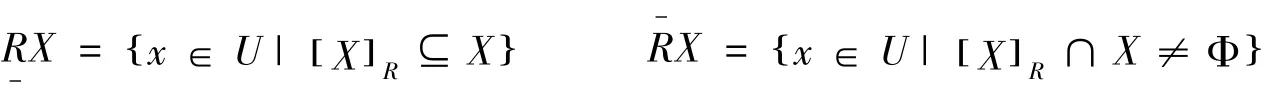
由等价关系R定义的集合X的近似精度如下:

粗糙集是刻画不确定性问题的一种手段，它在数据库知识发现、数据挖掘等领域都得到广泛的发展。它的特点是:无需借助于数据以外的先验信息就可对数据进行比较客观的处理。因此用粗糙集的思想能更客观的分析系统，具有较深刻的意义。

2 粗糙认知图

2.1 粗糙认知图定义

定义2 给定集合G={e1，e2，…em} ，顶点集V={v1，v2，…vn}。若赋予顶点属性后的边组成集合E=∪ek＜vi，vj＞，则称E是G的边集。称G=(V，E)是图，其中=m分别为顶点和边的个数。

2.2 粗糙认知图概念间权重的确定

边精度aR(T)用来反映人们对粗糙图T边集知识了解的完全程度。

由上述粗糙认知图的定义可知，两概念间存在有限多条边，并每条边都具有属性权值，基于认知图的应用，我们必须抽象出两概念间的一个综合关系，并赋予权值，以完成因果关系推理，基于此，我们给定:

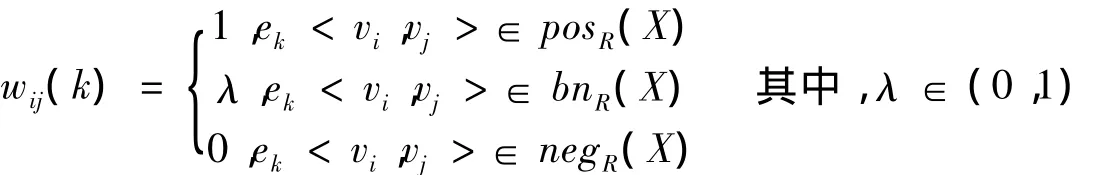
通过边界域与上下近似之间的关系，经整理得:ρij=λ+(1－λ)aR(T)

3 粗糙认知图模型

3.1 粗糙认知图时间模型(Rough Cognitive Map Time Model，RCMTM)

认知图及模糊认知图理论参见文献［7～14］。从这些文献可以看出，虽然FCM具有较多的优点，但它不能表示概念间的多种关系及关系测度对概念状态值的动态依赖关系，也不能表示概念间因果关系测度的不确定性。如图1所示，概念1与概念2之间的关系是多种多样的，概念自身的状态在变化，概念间的关系也是变化的。因此，其影响结果和程度肯定也会不同，从模糊认知图的角度出发考虑概念间的关系是不符合分析实际的。

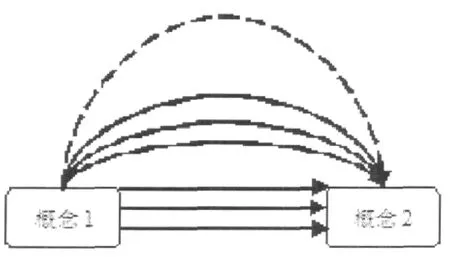
图1

Eugene等证明了若在环中加入时间的方向性，则环中各概念就不会出现相互依赖关系［15］。Stylios等在Kosko的模糊认知图模型中引入时间变量，为粗糙认知图奠定了理论基础［12～14］。

Stylios提出的具有时间及记忆状态的FCM可以表示为:

式中，Vcj(t)为概念cj在时间t的状态值，γ为上一时刻状态值对下一时刻时间状态值的影响因子。

如果用近似精度ρij来代替式(2)中的wij，即得到我们提出的具有记忆功能与动态特性的粗糙认知图时间模型(Rough Cognitive Map Time Model，RCMTM):

式中，随着时间得变化，通过等价关系Rij划分得到的等价类可能会发生变化，ρij随之改变以反映两概念间影响程度得大小。

对于图1，用ρij可以很容易解决用FCM表示时存在的问题。由于在ρij中引入了时间项，ρij(t)不仅能表现出“概念1”与“概念2”间因果关系确定－不确定性，还能表现出这种因果关系的动态特性，并由不同关系集合X的确定，通过计算得出不同的ρij(t)值。因此，RCMTM不仅继承了FCM的优点，还自然扩展了FCM的应用领域及模拟概念间关系的能力。

3.2 粗糙认知图时空模型(Rough Cognitive Map Space-Time Model，RCMSTM)

粗糙认知图时间模型建立了一个随时间变化的动态因果关系。实际上，概念间的关系除了会随着时间变化而变化外，往往与空间上概念的状态也是有关系的。如果我们在考虑因果关系时间特性的基础上，进一步考虑因果关系的空间特性，则得到粗糙认知图时空模型(Rough Cognitive Map Space－Time Model，RCMSTM)。其数学模型为:

式(4)这种表达方法不仅解决了FCM存在的缺陷，使得认知图不仅能处理概念间关系测度的不确定性，还对概念间因果关系的时空联系加以有效的整合。如图1中“概念1”对“概念2”的影响程度不仅与“概念1”的状态有关，而且与“概念1”的积累状态有关，表现为时间特性。同时影响程度还与空间上概念的状态等有关，表现为空间特性。这样就把关系测度的不确定性及联系的时空特性有效的融入粗糙认知图中，进一步扩展了粗糙认知图。

4 RCM的性质

定理2 (1)给定粗糙图T，对任一属性集R，都有0≤aR(T)≤1。

由以上定理可知，随着人们对粗糙图T边集X的知识了解完全程度的不同，反映在图中即为边属性集的丰富程度的不同，则边精度也会不同，从而边的综合权重也不同。

设C，V分别表示RCM的所有概念及概念状态值，R表示所有概念间具有直接因果关系的测度。

定理3(RCM概念间等价变换定理)

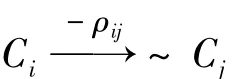
定理4 (RCM概念间动态测度等价关系定理)

在 RCM中若存在～Ci∈C，～Vi∈V，－ρij∈R，且ρij=λ+(1－λ)aR(T)，则－ρij(t)=1－ρij(t)。

上述两个定理具有很重要的实际意义，它可从一个RCM得到一个新的RCM，能指导我们对一个新系统因果关系的认识，并能减少较多工作量。

5 结束语

本文介绍了认知图模型和粗糙集的相关概念，为了克服认知图和模糊认知图的不足，本文提出了一种基于粗糙集理论的粗糙认知图模型。具有以下三点贡献:(1)肯定认知图中两概念间关系的多样性，更好的模拟现实生活中存在的问题;(2)不仅能表现出概念间关系确定－不确定性，还能表现出关系的动态特性;(3)对概念间关系的时空联系加以有效的整合;(4)针对认知图和粗糙认知图权值给定的主观性这一缺陷，综合边精度客观的给出两概念间的综合权重，使得粗糙认知图与模糊认知图相比计算量减小、复杂度降低。

关于粗糙认知图的研究目前尚处于探索阶段，还未形成相应的理论体系和系统的设计方法，存在许多的问题有待进一步研究与探索。

［1］Chaib-draa，B，J.desharnais.A relational model of cognitive maps［DB/OL］.http://citeseer.nj.nec.com/.2001，12.

［2］Axelrod R.Structure of Decision:the Cognitive Maps of Political Elites［M］.Princeton，NJ:Princeton University Press，1976.

［3］Kosko B.Fuzzy cognitive maps［J］.Int.J.Man-machine Studies，1986，24:65 ～75.

［4］Kosko B.Adaptive inference in fuzzy knowledge networks［C］.In:Proc.1st Int.Conf.Neural Networks，1987，2:261-26.

［5］骆祥峰，高隽.概率模糊认知图［J］.中国科学技术大学学报.2003，33(1):26-33.

［6］张文修.粗糙集理论和方法［M］.科学出版社，2001.

［7］Liu Z Q，Miao Y.Fuzzy cognitive map and its causal inference［J］.In:Proc.IEEE Int.Conf.Fuzzy Systems Seoul Korea，1999，3:1540-1545.

［8］Bart Kosko.Fuzzy Engineering［M］.Prentice Hall，1997.

［9］Liu Zhi-qing，Satur R.Contextual fuzzy Cogni tivemap for decision support in geographic informati-on systems［J］.IEEE transactions on fuzzy systems，1999，5(10):495-502.

［10］Satur R，Liu Zhi-Qing.A contextual fuzzy cogni-tive map framework for geographic information sytems［J］.IEEE transactions on fuzzy systems，1999，7(10):481-494.

［11］Thierry Marchant.Theory and methodology cognitive maps and fuzzy implications［J］.EuropeanJourn-al of Operational Research ，1999，114:626-637.

［12］Liu Zhi-qiang，Miao Yuan.Fuzzy cognitive map and its causal inferences［C］.IEEE international fuzzy systems conference proceedings.KoreaSeoul 1999，22-25.

［13］Stylios C D，Groumpos P P.Fuzzy Cognitive maps:a soft computing technique for intelligent control［C］.Proc.2000 IEEE International Sym-posium on intelligent control Italy Patras:Ju-ly 17-19，2000.97-102.

［14］Groumpos.P.P Stylios.C.D，Modelling supervisor ycontrol systems using fuzzy cognitive maps［J］.Chaos Solitons and Fractals ，2000，11:329-336.

［15］Eugene Santor Jr.Probabilistic temporal networks:A unified framework for reasoning with time and uncertainty ［DB/OL］.http://citeseer.nj.nec.com/.2001，12.