故障诊断信号的非平稳性

葛淼，玄兆燕

(河北联合大学机械工程学院，河北唐山 063009)

0 引言

随着设备状态监测和故障诊断研究的发展，所面临的关键问题之一是如何对监测诊断中得到的机械动态信号的非平稳性进行有效的分析。在机械设备监测诊断中，需要将非平稳信号进行平稳化处理，主要采用基于平稳过程的经典信号处理方法，分别从时域或频域给出统计平均结果，无法同时兼顾信号在时域和频域中的全貌和局部化，因此无法对信号的非平稳性进行有效的分析和处理。显然，研究处理非平稳性的实用方法是促使机械监测诊断不断发展的客观需要。

短时博里叶变换(STFT)缺乏细化能力，反映强烈瞬变信号的非平稳性功能不足;主分量自回归谱有一定的时频局部化功能，但对于非平稳信号分析能力不强;Wigner时频分布具有对准平稳或非平稳信号分析的功能，但是具有交叉干涉项［1］。小波变换具有良好的时频局部性，根据需要调整时间与频率分辨率，具有多分辨率分析的特点。其时频分析的结果同经典的分析方法有所不同，在高频范围内时间分辨率高，在低频范围内频率分辨率高，在全频带内正交分解的结果，信息量既无冗余也不疏漏，尤其适合分析时变非平稳信号［2，3］。

本文利用时间-指数法来对故障信号进行非平稳性判定，找出非平稳阶段，进而运用小波变换对非平稳信号进行分解和重构，有针对性地选取有关频带的信息，通过对重构信号的频谱分析，提取出故障的典型特征。通过对旋转机械的非平稳信号处理，证实了利用小波变换的方法进行故障诊断有很好的效果。

1 故障诊断信号的非平稳性分析

在信号处理中，平稳性主要是根据信号的统计量特征来衡量。若该信号各阶统计量与时间无关，则称该信号是平稳信号;若该信号某阶统计量随时间变化，则称该信号为非平稳信号。在机械设备监测诊断中，准确地分辨信号的平稳性至关重要，只有对信号进行了非平稳判定才能选择适合的分析方法和手段［4］。

1.1 时间-指数图法

在分析阶段，递归图法常被用来诊断非平稳性是否存在，本文将提供了一种崭新的方法——时间-指数法。它以在一组空间距离临近点为对象，检测以时间-指数ξ为函数的概率密度分布ρε(ξ)。基于重构相位空间的时域信息，在绝对时间域的不变测度里直接检测所测物理量的相关性。对无论是计算机生成或者实验确定的短时间序列数据进行检测，这种时间-指数方法能很清晰分辨动态非平稳性，且对嵌入参数不敏感［5］。时间-指数法算法如下:

1)假设我们观察一段长度为Ns的时域数据，并等间隔采样。将数据归一化，在［0，1］范围内生成一个新的序列 {Si:i=1，2，……，Ns}。

2)用延迟时间 τ组成的坐标系重构一个 m维相位空间A，并且创建N个嵌入向量{xi=［Si，S1+τ，……S1+(m+1)τ］T:i=1，2，……，N}∈A，其中上标T表示转置，N=Ns－(m－1)t。

3)在两点xi和xj之间定义时间-指数D为(xi≠xj)

其中T(xj)=i代表点xi沿轨迹的时间定位i。

4)对于一个参照点xi∈A，在给定的空间距离ε1内找到xi所有的附近点的集合:

5)得到全部xi和xj∈Ui(ε1)之间的时间指数。通过式(1)计算在参照点xi和向量xj∈Ui(ε1)之间的时间-指数D，从而得到全体N(ε)的时间-指数，其总个数为:

6)从时间-指数的最小值到最大值将全体数据平分(K+1)等份，创建一个归一化的概率密度分布函数:

式中，Nt=是全部计数总量，ξ∈［0，K］是标准化的时间-指数。

7)对于一个新的空间距离ε2，重复步骤3到6，得到相应的标准化概率密度分布ρε2(ξ)。对于不同空间距离εl(l=1，2……，L)，这个过程重复L次。

8)相对标准化时间指数ξ的L个空间距离，可绘出这些概率密度分布ρεl(ξ)。

1.2 非平稳信号的判定

测试对象选用转子实验台，实验设备有DRVI快速可重组虚拟仪器平台、加速度传感器(YD-37)、加速度传感器变送器和蓝津数据采集仪组成。分别在800r/min、1000 r/min、1300 r/min、1500 r/min和1700 r/min转速下测取正常转动、偏心转动的实验数据，并且在加速、匀速和减速各个运行阶段分别测取转子振动值。

运用时间-指数法来对震动数据进行非平稳性判定，通过时间-指数法的判别标准，对有限的时域信号，它的概率密度分布值接近于直线且波动很小，即为平稳信号;如果概率密度函数形状呈“V”型且具有一定程度上的幅值波动，说明此信号为非平稳信号。图1至图4分别给出了偏心转子在1000r/min时的减速阶段和匀速阶段、1300 r/min加速阶段和匀速阶段的转子振动值测试结果。

由图1至图4可见，加(减)速阶段的概率密度分布波动很大，其两端有很巨大的偏差，而匀速过程却平滑很多。说明转子变速过程中，它的振动信号是非平稳信号。由此可见，在变工况的旋转机械工作中，转子振动为非平稳性信号，可在这两个阶段进行非平稳性故障信号的分析研究。

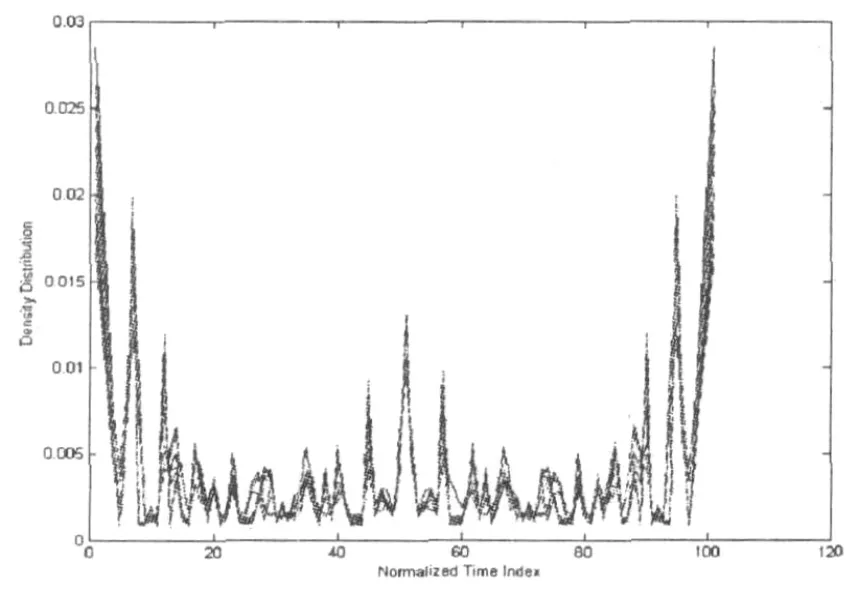
图1 1000 r/min减速阶段概率密度分布图

图2 1000r/min匀速阶段概率密度分布图

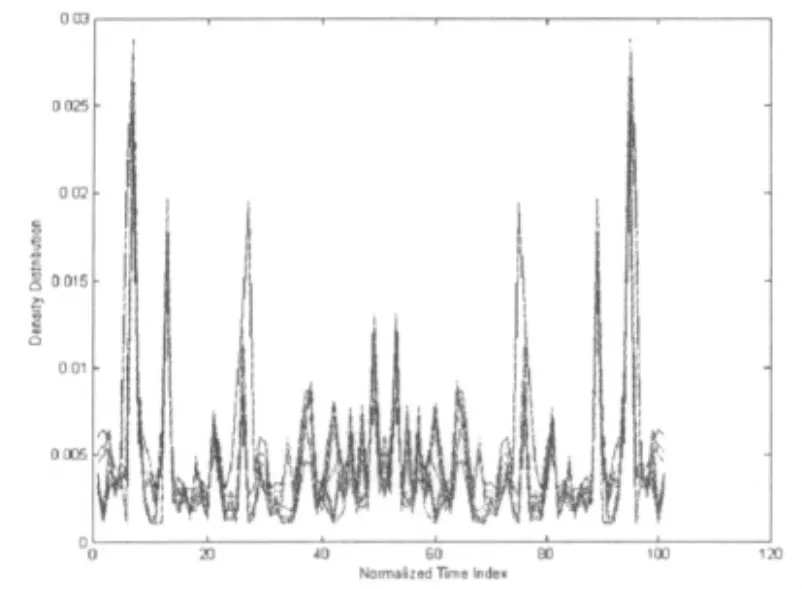
图3 1300 r/min加速阶段概率密度分布图

图4 1300 r/min匀速阶段概率密度分布图

2 非平稳性故障信号分析

2.1 小波基本理论

假设函数ψ(t)∈L2(R)，即平方可积，且积分平均等于零，则称ψ为一个基小波。将母小波经过伸缩和平移后，就可以得到一个小波序列:

式中，a，b∈R，且a≠0;a称为伸缩因子，b为平移因子。

在L2(R)中的闭子空间序列 {Vm}m∈Z∈l2为一个多分辨率分析，存在φ∈V0，将 { φ(t－k)}k∈Z构成的一个Riesz基，则总存在序列 {ck}k∈Z∈l2使得:

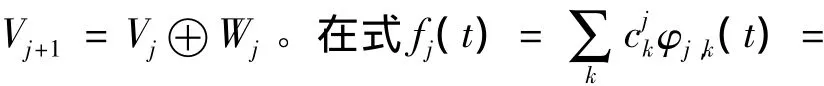
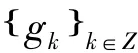
式中，表示滤波器h的共轭反转;cj*表示与的卷积;U、D分别表示二元上、下二抽样算子。小波分解与重构的迭代过程如图5所示。

图5 信号的小波分解与重构的迭代过程示意图

2.2 FFT与小波分析比较研究

对故障信号用db3正交小波进行五层小波分解，分解结果如图6所示，均为转速1300r/min时加速阶段的小波系数重构图，其中a1-a5为低频部分，d1-d5为高频部分。图6可以看出，原始振动信号很混乱，故障信号已经被噪声完全淹没。但是仔细观察高频重构的第三层会发现，波形有明显的周期性波动，于是我们对第三层高频重构部分进行频谱分析。同时，为了对比小波分析对非平稳信号的处理能力，我们采用经典的快速傅里叶变换直接对原始数据进行频谱分析，得到FFT频谱图如图7所示。

图6 加速阶段信号的小波重构图

图7 FFT频谱图

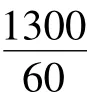
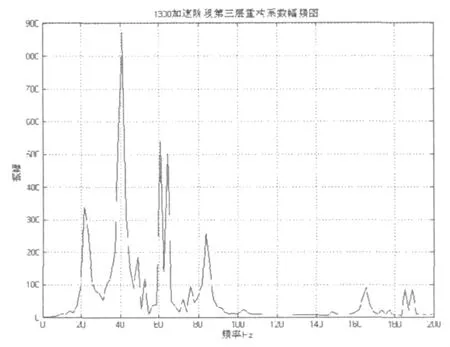
图8 加速阶段第三层重构系数频谱图

3 结论

介绍了非平稳信号的判定方法和小波分析对非平稳信号的故障诊断，采用时间-指数法确定其非平稳性，进而进行小波处理。通过对故障信号进行多尺度分解，分析各层小波系数，找出故障源。结果表明，时间-指数法很适用于信号的非平稳性判定，小波分析对非平稳性信号中故障的提取有着良好的效果。

［1］耿萌，石林锁.三种非平稳信号时频分析的方法［J］.机械工程与自动化，2008，(1):108-109.

［2］李弼城，罗建书.小波分析及其应用［M］.北京:电子工业出版社，2003.

［3］崔锦泰.小波分析导论［M］.程正兴译.西安:西安交通大学出版社，1995.

［4］张贤达，保铮.非平稳信号分析与处理［M］.北京:国防工业出版社，1998.

［5］Dejin Yu，Weiping Lu，Robert G.et al.Space time-index plots for probing dynamical nonstationarity［J］Physics Letters A，1998，250;323-327.