用Gleeble3500测塑性功转热系数的研究

李红斌，徐树成，邢满江，黄海端

(1.河北联合大学河北省现代冶金技术重点实验室，河北唐山 063009;2.河北任丘建投热电有限责任公司，河北 任丘 062550;3.河北联合大学迁安学院，河北唐山 064400)

0 引言

在金属材料的塑性加工过程中，塑性变形的同时常常伴随着金属温度随之升高的现象。在低应变率下的塑性变形通常处理成等温过程，在应变率为10－4～10－3s－1时试样受到拉伸，并没有表现出明显的温升现象［1］。而在高应变率时的变形过程往往可近似为绝热过程，且变形做功可转换成导致试件产生温升的热量，而温升往往导致材料软化［2］。MacdougallD等［3］人认为金属材料的塑性功转热系数η是一个介于0.8～1.0的常数。但也有文献［4］指出功转热系数低于该范围，发现功转热系数与塑性应变有关，并且极大地依赖于温度、应变和应变率。塑性变形功并不会完全转化为变形热，将会以位错、空位等形式部分储存于轧件内部(占2% ～5%)［5］;η通常取0.95～0.98之间［6］。在采用Gleeble3500进行压缩实验中，高速变形会出现试样温度快速升高，利用这种现象可以测定η的方法。

1 现象分析

在热模拟试验机上进行圆柱体单向压缩的试验中，常常伴随着温度在压缩瞬间有所冲高的现象，压缩过程中造成温度波动的原因主要有以下几个方面:

(1)压缩过程导致热电偶正负极之间的间距变大;

(2)由于试样在压缩过程中变短，截面变大，电阻变小;

(3)内外表面温度梯度造成的温度变化;

(4)在变形过程中，由塑性功转化为热，造成温度波动;

(5)试样截面变化，导致试样与砧子头的接触面积变大，热流变大。

即:

式中，ΔT为试样压缩时的温度波动值;dT1为热电偶间距变大造成的温度变化值;dT2为试样电阻原因造成的温度变化;dT3为试样内外温度梯度造成的温度变化值;dT4为塑性功转化成热导致的温度变化值;dT5为试样接触面积变大导致的温度变化值。

由(1)式可计算塑性变形导致的温度变化量，即:dT4，用dT4取代公式(2)中的ΔT［7］，求得转化系数。

式中，η为功热转化系数;ΔT为塑性功转化成热导致的温度变化值;c为试样在该条件下的比热容;ρ为试样在该条件下的密度;W为单位体积变形功。

2 材料与实验

2.1 实验材料

选用35#钢，用线切割机把试样切成Ф8 mm×15 mm的圆柱体试样，然后用砂纸磨光，确保表面光洁、无油渍、铁锈等;采用Ni－Cr(+)vsNi－Al(－)热电偶焊接，钽片、石墨片、陶瓷管等做压缩试验的耗材。

2.2 实验方案

试样以10℃/s加热到900℃，再以5℃/s加热到1150℃，保温5分钟后，以15℃/s的冷却速度到900℃并分别执行方案A、方案B和方案C。方案A:焊接两对热电偶，一对按照标准焊接，间距为1 mm，另一对间距为2 mm，冷却到900℃的时候保温10s，然后压缩;方案B:冷却到900℃时停止加热立即压缩;方案C:冷却到900℃的时候保温10s，立即停止加热立即压缩。压缩速率为10/s，压缩量为8mm，期间采集的数据有:TC1，TC3，strain，stress等，查看变形过程中TC1以及TC3所采集的温度变化;方案A中TC1，TC3分别为正常焊接的热电偶检测的温度和非标准焊接的热电偶检测的温度;方案B与方案C中TC1为正常焊接的热电偶检测的温度;strain，stress分别为应变与应力。

3 结果与分析

3.1 实验结果

执行方案A、方案B与方案C得到试验结果，试样温度随时间变化曲线如图1、图2、图3所示。

图1 方案A实测的温度-时间曲线

图2 方案B实测的温度-时间曲线

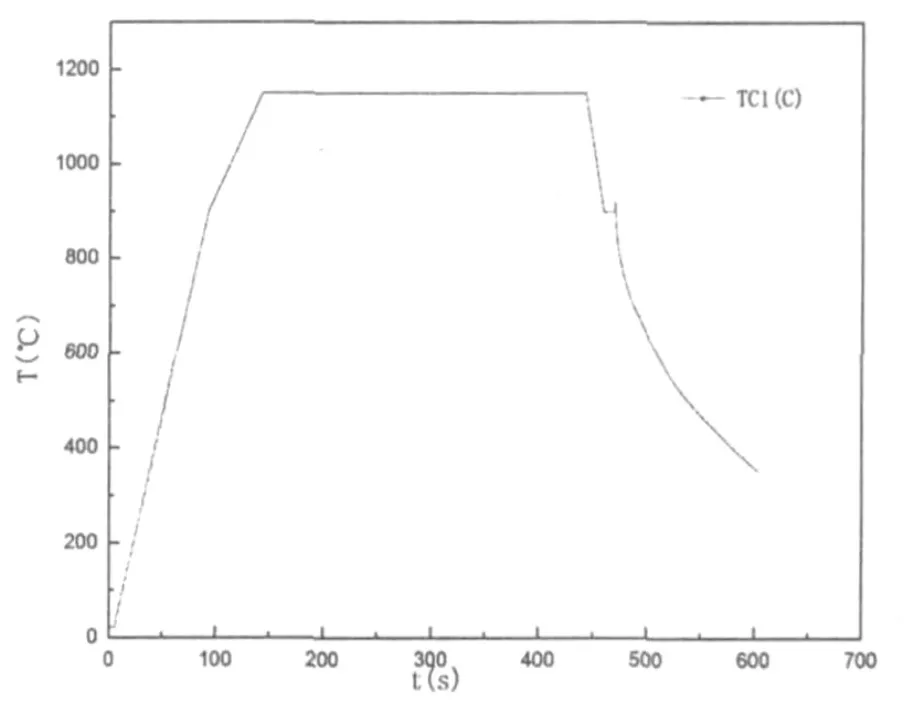
图3 方案C实测的温度-时间曲线

由图1、图2与图3可确定不同试验方案中的温度升高结果，如表1所示。

表1 各实验方案的温度升高结果

ΔT包含着以上五种因素的影响，下面分别对各影响因素进行分析。

3.2 结果分析

由于方案A与方案B的基本条件相同，把两个方案温度的弹跳值相减得:

式中，ΔTA，ΔTB分别是方案A与方案B的温度弹跳值;dT1A、dT1B分别为方案A、B热电偶间距变化对ΔT的影响;dT2A、dT2B分别为方案A、B试样电阻变化对ΔT的影响;dT3A、dT3B分别为方案A、B试样温度梯度对ΔT的影响;dT4A、dT4B分别为方案A、B机械功以及断面摩擦对ΔT的影响;dT5A、dT5B分别为方案A、B热电偶间距变化对ΔT的影响。

3.2.1 热电偶间距对ΔT的影响

在方案A的温度变化历程中，两对热电偶由于正负极间距不同造成的温度测量差别如图4所示。

TC1与TC3之间的最大温度差值是6℃左右，而且是发生在刚加热到1150℃的时候，当保温时温度差值变小，控制在5℃之内。在压缩的瞬间，dT1=TC1－TC3=2.62℃，可以确定在压缩后，由于TC1之间距离变大，约为2 mm，所以TC1测得的温度应该比实际温度低－2.62℃，仅就热电偶间距对ΔT的影响来说，方案A、方案B和方案C是相同的，即:

式中，dT1C为方案C中由于热电偶间距变化对ΔT的影响。

图4 TC1－TC3的温度差随TC1的变化关系

3.2.2 试样电阻变化对ΔT的影响

在试样压缩的过程中，由于方案A与方案B试验条件的差异在于，方案A在压缩过程中有电流，而在方案B与方案C中，则没有电流通过，所以在方案B中，不会产生由于试样电阻变化而导致的温度变化，即:

式中，dT2C为方案C中由于试样电阻变化对ΔT的影响。

3.2.3 试样温度梯度对ΔT的影响

由于在方案A与方案C中，均有10s的均温时间，所以方案A中试样可以忽略温度梯度对ΔT的影响，即:

式中，dT3C为方案C中由于温度梯度对ΔT的影响。

由表1可得，试样的内外温度梯度对温度波动的影响很小:

式中，ΔTC为方案C的温度弹跳值。

3.2.4 试样塑性功对ΔT的影响

三个方案中，变形条件相同，由机械功所造成的温度升高也是相同的，故有下式成立:

3.2.5 试样截面变化引起的热通量变化对ΔT的影响

由于方案A、方案B和方案C的基本条件相同，在变形过程中砧子头与试样接触，所以砧子头的温度也与试样的温度非常的接近，并且并行时间很短仅为0.0826s，由于断面变化不大，认为:

式中，dT5C为方案C中由于截面变化对ΔT的影响。

即由于试样断面变化引起热通量变化对ΔT的影响相等，且为零

综上所述:

可得由于电阻的因素对温度造成的影响为:

所以，可以确定由塑性功导致的温度上升值为:

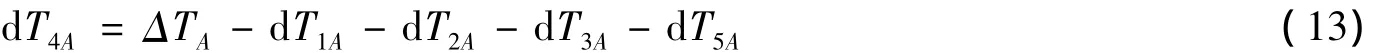
单位体积塑性功由式(14)计算［8］:

将(13)、(14)式代入(2)式，并由dT4A代替(2)式中的ΔT，可以得到:

4 结论

(1)压缩实验中，由于热电偶的间距变大会对温度检测造成影响，但影响很小。

(2)该方法是建立在利用热模拟试验机的平台之上，利用热模拟试验机的精准的控制能力实现其对温度及压缩量的合理控制，推导出由于塑性功导致的温度升高值;

(3)用热模拟试验机来测定功热转化系数是可行的，在本次实验的条件下测得的塑性功转化系数为0.97。

［1］张伟，肖新科，郭子涛，等.塑性功转热系数对钝头弹侵彻金属靶模拟结果的影响［J］.兵工学报，2010，31(1):168-171.

［2］MarcAndréMeyers.材料的动力学行为［M］.张庆明，刘彦，黄风雷，等译.北京:国防工业出版社，2006.

［3］Macdougall D.Determination of the plasticwork converted to heat using radiometry［J］.Experimental Mechanics，2000，4(3):298-306.

［4］Hayashi T，Yamamura H，kano S.Temperaturemeasurementofmetals underhigh velocity deformation［J］.Society of Materials Science，1977，Kyoto:94-98.

［5］William F H.Metal Forming Mechanics and Metallurgy［M］.Englewood Cliffs:Prentice-Hall Inc，1983.

［6］谢英杰，赵德文，韩立涛，等.高速线材精轧的等效应变研究及温升计算［J］.钢铁.2009，44(1):47-50.

［7］Richardson G J.Worked Examples in Metal Working［M］.London:The Chameleon Press Limited，1985.

［8］Arsenault R J，Beelar J R，Esterling D M.ComputerSimulationin Material science Seminar.ASM Material Science Seminar，Florida，ASM International，1988.