高速列车模型编组长度和风挡结构对气动阻力的影响
黄志祥,陈 立,蒋科林
(中国空气动力研究与发展中心 空气动力学国家重点实验室,四川 绵阳 621000)
高速列车模型编组长度和风挡结构对气动阻力的影响
黄志祥,陈 立,蒋科林
(中国空气动力研究与发展中心 空气动力学国家重点实验室,四川 绵阳 621000)
采用风洞试验的方法,分别对高速列车试验模型2~6车编组状态下的各节车厢气动阻力的分布规律,以及2种不同结构外形的风挡对3车编组列车模型各节车厢气动阻力的影响进行了研究。结果表明:当编组长度大于3车,头车、尾车的阻力系数随编组长度的增加变化较小,中间车的阻力系数约为0.1。1节头车+N节中间车+1节尾车的全车气动阻力系数,可用3车编组模型试验的头车阻力系数+0.1×N+尾车阻力系数之和进行估算。高速列车风洞试验模型分别采用风挡1和风挡2两种风挡,只是使得气动阻力在各节车厢之间形成不同的分配,对由各节车厢相加形成的全车气动阻力的试验结果影响很小。
高速列车;编组;风挡;气动阻力;风洞试验
0 引 言
随着高速列车运行速度的提高,运行阻力越来越大,且运行速度越高,气动阻力在总运行阻力中的比重越来越高[1-2]。因此,研究气动阻力及减阻措施对于高速列车的节能降耗具有非常重要的意义。目前,研究高速列车气动阻力的手段主要有风洞试验、数值计算和实车路试。其中,风洞试验是数值计算最常见的验证依据提供者,也因为易于控制、可实现更多工况的研究而比实车路试更为方便和有效,因此,风洞试验是目前高速列车气动阻力最常用和有效的研究手段[3-4]。
在包括气动阻力在内的高速列车空气动力学风洞试验研究中,由于风洞试验模拟的特殊性,在实际研究过程中气动阻力存在着受到模拟方式影响的问题。一是由于受到风洞试验段尺寸尤其是长度的限制,通常采用短编组(国内通常采用3车编组)进行高速列车气动阻力的模拟,而实际高速列车通常是6车、8车或16车编组。研究表明,气动阻力与编组情况密切相关,因此,如何将短编组的气动阻力结果推广到长编组的气动阻力是一个非常现实的问题[5-6]。二是研究人员通常需要分别获得高速列车各节车厢(头车、中间车和尾车)气动阻力的分布,为此,在实际模拟过程中,试验模型的各节车厢是相互独立的单元,彼此分开,以实现对各个独立单元气动阻力的单独测量,由此就带来了各独立单元之间风挡结构的模拟问题。风挡结构外形不同,对各独立单元的气动阻力的大小以及气动阻力在各节车厢之间的分配具有非常明显的影响,因此,如何对高速列车风洞试验模型各节车厢之间的风挡结构和外形进行合理模拟,是高速列车气动阻力风洞试验研究中另一个非常重要和现实的问题。
采用风洞试验的方法,研究不同编组长度和风挡结构对高速列车气动阻力的影响规律,为高速列车气动阻力的风洞试验研究中面临的上述问题提供适用、有效的工程方法。
1 试验研究概况
1.1 试验设备
试验研究在中国空气动力研究与发展中心8m×6m/12m×16m风洞第二试验段进行。风洞试验段宽8m,高6m,长15m,如图1所示。试验段安装了列车试验专用地板装置。列车试验地板装置由5块板拼接而成,地板上表面距风洞下洞壁1.06m,地板中间为直径7m、可旋转360°的转盘,地板采用被动式边界层吸除方式,可有效降低地板边界层厚度。安装列车试验地板后,试验段变为长16.1m、宽8m、高4.94m、有效截面积39.2m2。
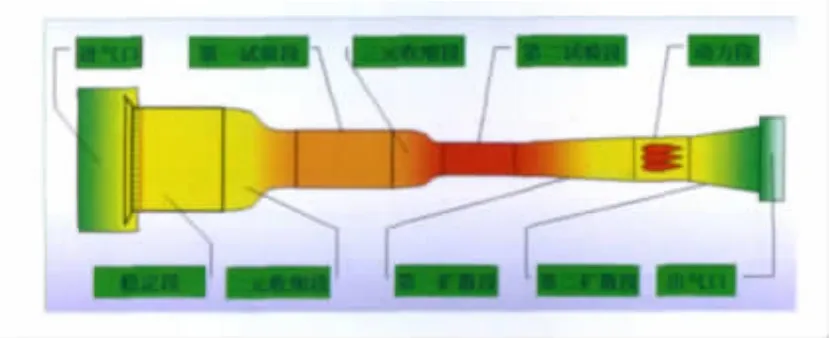
图1 8m×6m/12m×16m风洞结构图Fig.1 Structure of 12m×16m/8m×6mwind tunnel
1.2 试验模型
高速列车试验模型比例分别为1∶8和1∶15,头车和尾车流线型长度换算为实车约为12m,全车参考面积换算为实车约为9.5m2。1∶8模型为3车编组:头车、1节中间车和尾车,模型总长度约9.7m。1∶15模型分别为2车编组(头车+尾车)、3车编组(头车+1节中间车+尾车)、4车编组(头车+2节中间车+尾车)、5车编组(头车+3节中间车+尾车)、6车编组(头车+4节中间车+尾车)。列车中间车无受电弓,3车以上编组的中间车是相同的,列车头、尾外形完全相同。不同编组列车模型和各节车厢名称标示如图2。1∶15和1∶8列车模型各节车厢之间分别约有3和5mm的间隙,保证相互独立,以实现各节车厢的单独测力。
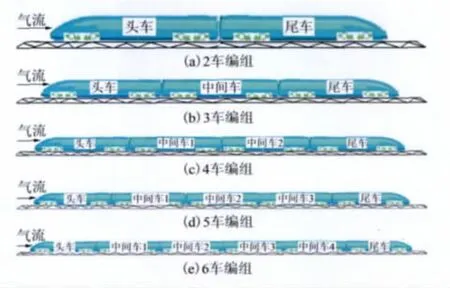
图2 不同长度编组列车模型示意图Fig.2 Different length of train formation of train models
列车模型通过连接件支撑在平地路基和轨道上,转向架车轮下表面高度与轨道上表面高度相同,且列车模型与路基、轨道不接触。路基中间部位固定在试验段转盘之上,两端安装有滑轮,整个列车模型和路基轨道可以随转盘同步转动。平地路基和轨道模型长约14m,前后端伸出列车头车、尾车的长度不小于2m。
1.3 研究内容
为了研究高速列车模型在不同编组长度状态下各节车厢的气动阻力分布规律,对于1:15模型,分别进行2车编组、3车编组、4车编组、5车编组和6车编组在试验侧偏角为0°(无侧风)、试验风速30~65m/s的条件下各节车厢的气动阻力测量试验。为了研究不同风挡结构对列车模型气动阻力的影响,对1∶8模型在3车编组状态下分别采用了两种风挡结构,在试验风速为60m/s、试验侧偏角0°~30°的条件下进行各节车厢气动阻力的测量试验。在风挡1的外形结构中,其高度约为314mm,一半厚度约为28mm,且相邻两节车厢外风挡表面形成对称的内凹,收缩角约为22.5°;在风挡2的外形结构中,除了采用嵌套结构外,相邻两节车厢外风挡表面是平直过渡的。两种风挡结构如图3和4所示。

图3 风挡结构1Fig.3 Vestibule diaphragm structure 1

图4 风挡结构2Fig.4 Vestibule diaphragm structure 2
1.4 研究方法
试验采用多天平分别对高速列车模型各节车厢同时测量气动力的方案,测量气动力的盒式六分量应变天平位于模型各节车厢空腔内,如图5所示。列车模型各节车厢分别单独测量气动力。

图5 试验模型内部安装的天平Fig.5 The balance installed in testing model
高速列车模型全车的气动阻力为各节车厢气动阻力之和。例如,3车编组全车气动阻力=头车气动阻力+中间车气动阻力+尾车气动阻力。
2 研究结果和分析
2.1 不同编组长度对气动阻力的影响
图6和表1分别给出了1∶15模型的2~6车编组状态下列车模型各节车厢气动阻力系数试验结果的比较。
从图6和表1的试验结果可以看出,不同编组长度列车模型各节车厢的阻力系数基本是随着风速的增加略有变化,且试验风速大于40m/s后,气动阻力系数随试验风速的增加变化很小,基本趋于稳定。
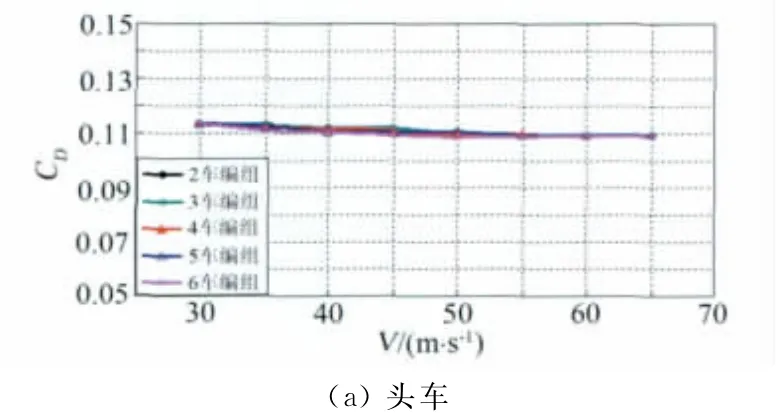

图6 不同编组列车的各节车厢气动阻力结果比较Fig.6 Comparison of aerodynamic drag results of each car of different train formation
在2~6车编组状态下,在相同的试验风速时,不同编组长度列车的头车阻力系数约为0.11左右,不同编组状态下头车的阻力系数差异很小。当编组长度为3车及以上时,第1节中间车的阻力系数约为0.08左右,其中3车编组的第1节中间车(仅有1节中间车)阻力系数略大于0.08,比其它编组的第1节中间车阻力系数略大,但4~6车编组的第1节中间车的阻力系数差异较小,且略小于0.08。这可能是因为3车编组的第1节中间车后紧邻尾车,受尾流影响比4~6车编组的第1节中间车(其后紧邻等截面中间车)大,因此阻力系数偏大。当编组长度为4~6车时,第2节中间车的阻力系数约为0.10,且随编组长度的增加变化很小。当编组长度为5~6车时,第3节中间车的阻力系数约为0.10,同样随编组长度的增加变化很小。当6车编组时,第4节中间车的阻力系数约为0.10,与第3节中间车的阻力系数基本接近。在2~6车编组状态下,2车编组的尾车阻力系数约为0.17,3~6车编组的尾车阻力系数约为0.18,即2车编组的尾车阻力系数稍小于3车及以上编组的尾车阻力系数。

表1 不同编组列车的各节车厢气动阻力结果比较Table 1 Comparison of aerodynamic drag results of each car of different train formation
由此可见,当风速条件相同,在不同长度的编组状态下,头车的气动阻力基本变化很小,即不同长度的编组对头车阻力影响很小。当编组长度大于3车,第1节中间车的阻力系数比其它中间车的阻力系数略小,第1节中间车之后的其它中间车阻力系数差异较小。3车及以上编组状态下的尾车阻力系数略大于2车编组的尾车阻力系数,而且,当编组长度不少于3车(即中间车不少于1节),则尾车阻力系数随编组长度的增加略有变化,但变化很小。因此,根据上述编组长度对阻力试验结果的影响规律可以推测,在没有受电弓的状态下,1节头车+N节中间车+1节尾车的全车气动阻力系数可以用3车编组试验的头车阻力系数+0.1×N+3车编组试验的尾车阻力系数进行估算。从而用工程方法初步解决了短编组风洞试验的气动阻力结果推广到长编组全车气动阻力的问题。
2.2 不同风挡结构对气动阻力的影响
表2给出了1∶8模型在不同风挡结构状态下试验风速为60m/s的各节车厢气动阻力系数试验结果的比较。
从表2的数据比较可以看出,在0°侧偏角(无侧风)下,安装风挡1的头车、中间车、尾车和全车的阻力系数分别约为0.09、0.075、0.21和0.38,安装风挡2的头车、中间车、尾车和全车的阻力系数分别约为0.12、0.076、0.18和0.38。即风挡1状态的头车阻力系数比风挡2的小,中间车阻力系数与风挡2的接近,尾车阻力系数比风挡2的大,全车阻力系数与风挡2的接近。这是因为采用风挡1之后,相邻两节车厢外风挡表面形成对称的内凹外形,气流从前向后流动至此后受到内凹风挡向下的诱导,进入两节车厢(头车与中间车、中间车与尾车)风挡处的缝隙空腔内,在空腔内形成一个类似弹簧产生的作用力,分别作用在形成空腔的前后两节车厢上,使前车厢阻力减小,后车厢阻力增大,即头车阻力减小,尾车阻力增大,中间车因为前后分别受到一个向后和向前的作用力,互相抵消,因而阻力变化很小。
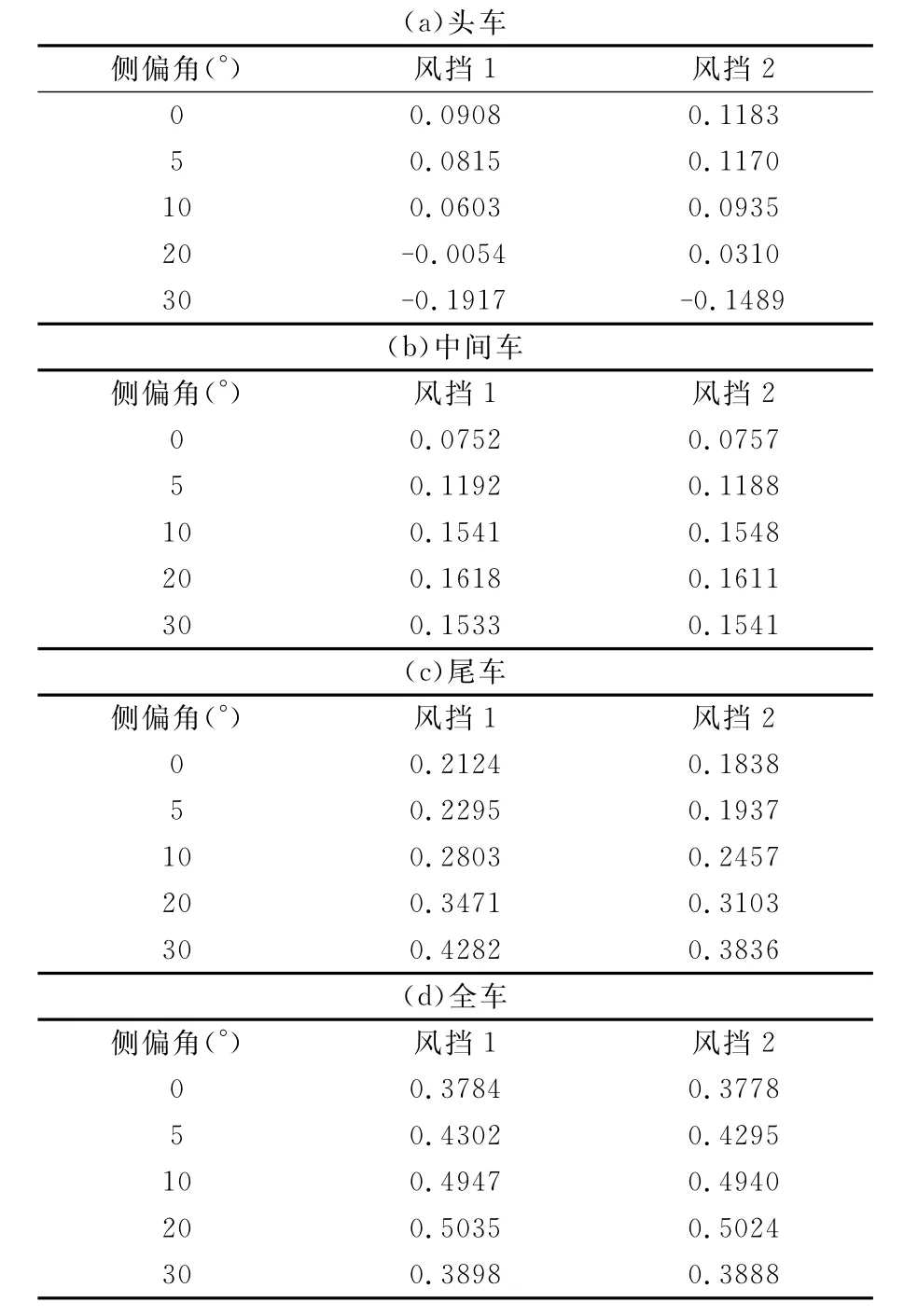
表2 不同风挡结构的列车各节车厢气动阻力结果比较Table 2 Comparison of aerodynamic drag results of each car of different structure of vestibule diaphragm
当侧偏角不为0°时,在相同的试验侧偏角下,同0°侧偏角类似,风挡1的头车阻力系数比风挡2的小,中间车阻力系数与风挡2的差异较小,尾车阻力系数比风挡2的大,全车阻力系数与风挡2的接近。
由此可见,高速列车风洞试验模型采用上述两种风挡结构,只是使得气动阻力在各节车厢之间形成不同的分配,对由各节车厢相加形成的全车气动阻力的试验结果影响很小。但是,从气动阻力在各节车厢的分配合理性上来说,风洞试验中的模型建议还是采用风挡2结构。主要原因有两点:一是风挡1对车身表面流经风挡处的气流进行导流而形成干扰,从而放大了各节车厢风挡间隙的影响。尽管风挡1向内收缩的外形结构在一定程度上与高速列车实车近似,然而,高速列车实车相邻两节车厢的(外)风挡是紧密连在一起的,之间并没有缝隙。而高速列车试验模型为了实现对各节车厢气动力的独立测量,在风洞试验研究过程中,必须保证各节车厢之间相互独立,互不干涉,于是人为地将各节车厢分离开,使得相邻两节车厢风挡处保持一定距离的间隙(1∶8模型的间隙约为5mm),这是高速列车多编组模型风洞试验目前无法避免的一个固有问题;二是风挡1使得头车与中间车的阻力系数更接近而不太合理,因为从高速列车各节车厢实际气动力的形成和分配来看,头车的气动阻力主要由压差阻力和摩擦阻力构成,中间车的气动阻力主要由摩擦阻力构成,头车气动阻力明显比中间车气动阻力大才更合理[7]。而采用风挡2结构,尾车的气动阻力最大,中间车的气动阻力最小,头车的气动阻力明显比中间车的大,这种气动阻力分配规律得到了大量高速列车模型表面压力测量的风洞试验结果的验证。
3 结 论
通过风洞试验的方法,研究了不同编组长度和风挡结构对高速列车气动阻力的影响规律,得到了以下结论:
(1)对于不同编组长度的高速列车模型,不同编组长度对头车阻力的影响很小;当编组长度大于3车,第1节中间车的阻力系数比其它中间车的阻力系数略小,且其它中间车阻力系数差异较小;2车编组的尾车阻力系数稍小于3车及以上编组的尾车阻力系数,3车及以上长度编组的尾车气动阻力随编组长度的增加变化很小。
(2)1节头车+N节中间车+1节尾车的全车气动阻力系数,可用3车编组模型试验的头车阻力系数+0.1×N+尾车阻力系数进行估算。
(3)在相同的试验侧偏角下,风挡1状态下的头车阻力系数比风挡2状态下的小,中间车阻力系数与风挡2状态下的差异较小,尾车阻力系数比风挡2状态下的大,全车阻力系数与风挡2状态下的接近。
(4)高速列车风洞试验模型分别采用风挡1和风挡2两种风挡,只是使得气动阻力在各节车厢之间形成不同的分配,对由各节车厢相加形成的全车气动阻力的试验结果影响很小。从高速列车各节车厢气动力分配合理性的角度出发,风洞试验模型建议采用风挡2结构。
[1]梁习锋,田红旗,邹建军.动力车纵向气动力风洞试验及数值模拟[J].国防科技大学学报,2003,25,(6):101-105.
[2]李明.高速列车空气动力性能风洞试验研究方法[D].南京航空航天大学,2001.
[3]田红旗.列车空气动力学[M].北京:中国铁道出版社,2007.
[4]田红旗,高广军.270km·h-1高速列车气动性能研究[J].中国铁道科学,2003,24(2):14-18.
[5]田红旗.列车编组方式对运行空气阻力的影响[J].机车电传动,2000,7(4):9-11.
[6]张健.降低铁路专用平车空气阻力的试验研究[J].铁道车辆,2000,38(6):1-3.
[7]HEINE C,MATSCHKE G.The influence of the nose shape of high speed trains on the aerodynamic coefficient[C].World Congress on Railway Research,Germany,2001.

黄志祥(1980-),男,湖北黄陂人,助理研究员。研究方向:车辆空气动力学。通讯地址:四川省绵阳市中国空气动力研究与发展中心 (621000),E-mail:xjtu331hzx@163.com
Influence of length of train formation and vestibule diaphragm structure on aerodynamic drag of high speed train model
HUANG Zhi-xiang,CHEN Li,JIANG Ke-lin
(State Key Laboratory of Aerodynamics,China Aerodynamics Research and Development Center,Mianyang Sichuan 621000,China)
The wind tunnel test is carried out to study the distribution regularity of aerodynamic drag of each car of the high speed train models from 2-car to 6-car formation,and the affect of 2types of vestibule diaphragm structure on aerodynamic drag on each car of the train model under 3-car formation.The results indicate:while the train formation is more than 3,the changes of drag coefficients of head car and tail car are little with increase of the number of train formation,and the drag coefficients of middle cars are about 0.1.The drag coefficient of entire train under the formation of 1head car plus N middle cars plus 1tail car could be estimated by sum of 1head car plus 0.1×N plus 1tail car drag coefficient results of 3-car formation.The different distributions of aerodynamic drag among each car of the high speed train model are caused by two different types of vestibule diaphragm 1and 2,but the affect of vestibule diaphragm structure on aerodynamic drag of the entire train is small.
high speed train;train formation;vestibule diaphragm;aerodynamic drag;wind tunnel test
V211.74
A
1672-9897(2012)05-0036-06
2011-09-20;
2012-02-20

