基于端点区域分布的圆形窗口线裁剪算法

任洪海

(大连交通大学 软件学院，辽宁 大连 116052)

0 引言

圆形窗口线裁剪拥有很强的实用价值，人们一直努力寻求高效的裁剪算法［1-6］.确定线段是否与圆形窗口相交是该类算法的关键.很多算法都引入窗口圆的外切正方形与内接正方形作为预处理操作.一般外切正方形指四边分别平行于坐标轴且与圆相切的正方形;而内接正方形指四边分别平行于坐标轴且包含在圆内部的最大正方形.这样定义往往只能独立确定一部分完全在外切正方形之外和完全在内接正方形之内的特殊线段，后续还需进一步判断剩余的线段.多数算法为此都应用了较为烦琐的辅助操作.例如，文献［3］中的旋转矢量法、文献［4］中制备规范化交点表、文献［5］需要进行多重编码、文献［6］中几何变换和逆变换等都需要花费很大精力.本文通过巧妙地定义外切正方形与内接正方形使圆心为坐标原点的圆形窗口在四个象限的圆弧分别位于四个三角区域，将其定义为角区.由此，将裁剪窗口所在平面划分为内接正方形之内、外切正方形之外和角区三部分.根据线段两端点在不同区域的分布情况完成裁剪过程.在裁剪过程中很多较复杂的判断都转化为线段所在直线与角区外界的相交情况进行处理，通过简单判别快速确定线段是否与圆形窗口相交，从而显著提高裁剪效率.

1 理论基础

不失一般性，假设裁剪算法中圆形窗口的圆心为坐标原点，半径为r;被裁剪线段的两个端点为 p1(x1，y1)和 p2(x2，y2).

定义1 本文中的“外切正方形”指四边平行于坐标轴，且与圆相切的正方形.

点在外切正方形之内(或上)的判断条件为:︱x︱≤r且 ︱y︱≤r;

点在外切正方形之外的判断条件为:︱x︱ ＞r或 ︱y︱ ＞ r.

定义2 本文中的“内接正方形”指顺序连接外切正方形与圆的四个切点所形成的正方形.

点在内接正方形之内(或上)的判断条件为:︱x︱ +︱y︱≤r;

点在内接正方形之外的判断条件为:︱x︱ +︱y︱ ＞ r.

定义3 在外切正方形之内(或上)且内接正方形之外的四个等腰直角三角形区域分别定义为角区，并根据所在象限区分为:第Ⅰ角区、第Ⅱ角区、第Ⅲ角区、第Ⅳ角区，如图1.

定义4 每个角区的两条直角边称为角区外界.角区外界根据各自所属角区进行区分，四个角区所有的角区外界构成整个外切正方形.如果有直线相交于角区外界，可以根据交点坐标的符号确定是相交于相同角区外界还是相异角区外界.

图1 线段裁剪部分示例图

定义5 如果端点在某角区内，进一步判断端点与圆形窗口的位置关系:如果端点在圆形窗口之内(或上)，称该点在内角区;如果端点在圆形窗口之外，称该点在外角区.

定理1 如果一条直线相交于两相异角区外界，则该直线一定与圆形窗口相交.

证明:不失一般性，假设直线相交于第一角区水平角区外界，设交点为I1(如图1中线段a所在直线)，过该点向圆形窗口作切线.其中一条是与外切正方形部分水平边重合，而另一条切线一定与第一角区垂直外界相交，设交点为I2.如果过I1点的直线与圆外切正方形相交于两相异角区外界，则该直线一定在两切线之间，因而与圆形窗口相交.

由定理1可推导出以下结论:

结论1 如果线段两端点分别在两相异外角区，可得线段一定与圆形窗口相交(如图1中线段b).

结论2 如果线段一端点在外角区，另一端点在外切正方形之外，且线段相交于端点所在角区的相异角区外界，可得线段一定与圆形窗口相交(如图1中线段c).

结论3 如果线段两端点都在外切正方形之外，且线段相交于两相异角区外界，可得线段一定与圆形窗口相交(如图1中线段a).

结论4 如果线段一端点在外角区，另一端点在外切正方形之外，线段相交于本角区外界但延长外角区内端点后延长线相交于相异角区外界，可得线段一定不与圆形窗口相交(如图1中线段d).

结论5 如果线段两端点分别在同一外角区内，并且线段所在直线相交于不同角区外界，可得该线段一定不与圆形窗口相交(如图1中线段e).

结论1～3由定理1很容易推出，结论4与结论5证明过程为:两种情况都是线段所在直线相交于不同角区外界，根据定理1，线段延长后的直线与圆形窗口相交，而线段两端点都在两交点的同侧，因而该线段本身一定不与圆形窗口相交.

以上结论所涉及的线段可以归纳为线段所在直线相交于不同角区外界的各种情况.当线段所在直线与某角区两角区外界相交时，可根据该角区外界上两个交点坐标判断线段所在直线是否与圆形窗口相交.下面以线段相交于第Ⅰ角区两角区外界为例讨论该线段与圆形窗口的位置关系.

对于任意相交于第Ⅰ角区外界的线段f，两交点为I1(xT，r)，I3(r，yR).可以取两个交点任意一个，过该点作圆形窗口的切线.假设取I1，作圆形窗口的切线，与第Ⅰ角区垂直方向角区外界的交点设为I2(r，y'R)(如图1)，根据切线长定理有:

由于相交于第Ⅰ角区外界，将上面两个公式整理可得:xT×y'R=r2－(xT+y'R)r，由此求出:

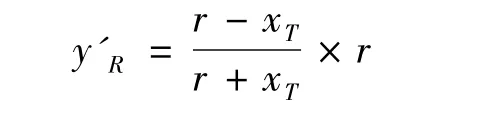
比较yR与y'R的大小可得线段f与圆形窗口的位置关系:

如果yR＞y'R，可得线段f与圆形窗口相离;

如果yR=y'R，可得线段f与圆形窗口相切;

如果yR＜y'R，可得线段f与圆形窗口相交;

对于相交其它两角区外界的线段，同样可进行类似推导，并得出相应结论，在此不再描述.

2 算法描述

根据被裁剪线段两端点区域分布情况裁剪过程讨论如下:

(一)如果线段两端点都在内接正方形之内，可得线段完全在圆形窗口之内，保留该线段作为裁剪结果，如图2中线段a.

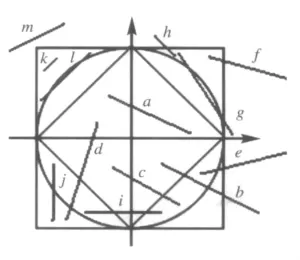
图2 线段裁剪部分示例图

(二)如果线段一端点在内接正方形之内，而另一端点在外切正方形之外，可得线段与圆形窗口相交，求交点.内接正方形之内的端点到交点间线段为裁剪结果，如图2中线段b.

(三)如果线段一端点在内接正方形之内，而另一端点在角区内，进一步判断角区内的端点在内角区还是外角区.

(1)如果端点在内角区，可得线段完全在圆形窗口之内，保留该线段作为裁剪结果，如图2中线段c.

(2)如果端点在外角区，可得线段与圆形窗口相交，求交点.内接正方形之内的端点到交点间线段为裁剪结果，如图2中线段d.

(四)如果线段一端点在角区，而另一端点在切正方形之外，进一步判断角区内的端点在内角区还是外角区.

(1)如果端点在内角区，可得线段与圆形窗口相交，求交点.角区内端点到交点间线段为裁剪结果，如图2中线段e.

(2)如果端点在外角区，线段一定与某角区外界相交，判断是否相交于内端点所在角区外界.

①如果线段相交于相异角区外界，根据结论2可得线段一定与圆形窗口相交，两交点间线段为裁剪结果，如图1中线段c.

②如果线段相交于本角区外界但延长线相交于其它角区外界，根据结论4可得线段一定不与圆形窗口相交，如图1中线段d.

③如果线段所在直线相交于内端点所在角区外界，求线段所在直线与该角区两角区外界的交点，设交点为I1、I2，判断线段I1I2与圆形窗口的位置关系:

a.如果I1I2与圆形窗口相离，可得线段不与圆形窗口相交，无裁剪结果输出，如图2中线段f.

b.如果I1I2与圆形窗口相交或相切，判断两端点p1、p2与线段p1p2主射线的位置关系.

如果两端点p1、p2分别在线段p1p2主射线的两侧，方法为:

如果min(y1/x1，y2/x2)＜ (x1－x2)/(y2－y1)＜max(y1/x1，y2/x2)，线段与圆形窗口有交点，交点间线段为裁剪结果，如图2中线段g.

否则线段与圆形窗口无交点，无裁剪结果输出，如图2中线段h.

(五)如果线段两端点都在角区，进一步判断两端点在内角区还是外角区.

(1)如果两端点都在内角区，则线段完全在圆形窗口内，保留该线段作为裁剪结果，如图2中线段 i.

(2)如果一个端点在内角区，另一个端点在外角区，则线段与圆形窗口有一交点，内角区内端点到交点间线段为裁剪结果，如图2中线段j.

(3)如果两个端点都在外角区，根据端点所在象限区分是否在相同外角区:

①如果两端点分别在不同外角区，根据结论1可得线段与圆形窗口有两个交点，交点间线段为裁剪结果，图1中线段b.

②如果两端点在同一外角区，测试线段所在直线与外切正方形的相交情况:

a.如果相交于不同角区外界，根据结论5可得线段不与圆形窗口相交，无裁剪结果输出，如图1中线段e.

b.如果相交于同一角区外界，设交点为I1、I2，判断线段I1I2与圆形窗口的位置关系:

c.如果I1I2与圆形窗口相离，可得线段不与圆形窗口相交，无裁剪结果输出，如图2中线段k.

d.如果I1I2与圆形窗口相交或相切，判断两端点p1、p2与线段p1p2主射线的位置关系:

如果两端点p1、p2分别在线段p1p2主射线的两侧，方法为:

如果min(y1/x1，y2/x2)＜ (x1－x2)/(y2－y1)＜max(y1/x1，y2/x2)，线段与圆形窗口有交点，交点间线段为裁剪结果，如图2中线段l.

否则线段与圆形窗口无交点，无裁剪结果输出，如图2中，在线段h上取角区内一小线段.

(六)如果两个端点都在外切正方形之外.进一步判断线段与外切正方形的相交情况.

(1)如果线段不与外切正方形相交，可得线段一定不与圆形窗口相交，即无裁剪结果输出，如图2中线段m.

(2)如果线段与外切正方形相交于两不同角区外界，可得线段一定与圆形窗口相交，两交点间线段为裁剪结果，如图1中线段a.

(3)如果线段与外切正方形相交于同一角区外界，设两交点为I1、I2，判断线段I1I2与圆形窗口的位置关系:

①如果I1I2与圆形窗口相离，可得线段不与圆形窗口相交，无裁剪结果输出，如图1中线段f.

②如果I1I2与圆形窗口相交或相切，可得线段与圆形窗口有交点，交点间线段为裁剪结果，如图1中线段g.

3 结论

作为圆形窗口线裁剪算法，快速确定线段与圆形窗口的相交情况是提高效率的关键.本文提出的新算法在未增加其它复杂辅助操作前提下，通过判断被裁剪线段两端点相对于外切正方形与内接正方形所划分的不同区域情况完成裁剪过程.在算法中通过角区及角区外界等概念的引入，首次提出根据被裁剪线段相交于外切正方形及内接正方形的情况直接确定是否与圆形窗口相交，避免大量不必要的求交运算及其它辅助操作.同时，新算法设计简单，容易实现.应用C++编程实现文献［4-6］及本文算法，附表列出四个裁剪算法对于不同半径圆形窗口裁剪300万条随机线段所需的时间比较.

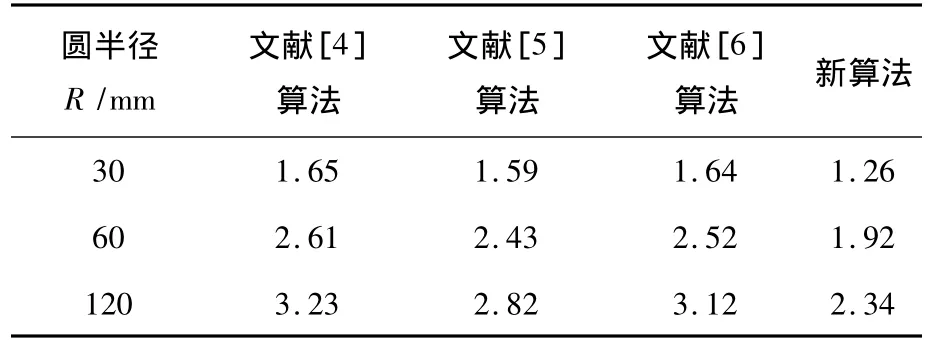
附表 种裁剪算法裁剪300万条线段所需时间比较 s

由附表可以看出新算法的裁剪效率都高于现有的三个典型算法.

［1］姚涵珍，宋鹏，张国安.圆形窗口裁剪算法的研究与实践［J］.计算机辅助设计与图形学学报，1992，4(3):14-20.

［2］刘勇奎.圆形及椭圆形裁剪窗口［J］.计算机工程与设计，1994，15(4):33-37.

［3］沈庆云，周来水，周儒荣.一种圆形窗口裁剪的新方法［J］.计算机辅助设计与图形学学报，1997，9(6):538-542.

［4］蔡敏，袁春风，宋继强，等.一种快速的圆形窗口裁剪算法［J］.计算机辅助设计与图形学学报，2001，13(12):1063-1067.

［5］陆国栋，邢军伟，谭建荣.基于多重编码技术的圆形窗口线裁剪算法［J］.计算机辅助设计与图形学学报，2002，14(12):1133-1137.

［6］唐棣，单会秋.一种基于坐标变换的圆形窗口线裁剪算法［J］.计算机应用与软件，2006，23(5):116-118.