跨阻滤波器的快速实用设计

高凤霞，杨朝龙，滕建辅

（天津大学 电子信息工程学院，天津 300072）

电压模式滤波器的设计理论和设计方法已经非常成熟，并被广泛地应用于信号处理中。然而，随着物联网的快速发展，传感器将被广泛地应用于信号采集，而许多传感器的输出是电流信号。如果需要对传感器输出的电流信号进行滤波，则要用到电流模式滤波器，滤波后再将输出的电流信号转换为电压信号进行后续处理。将输入的电流信号转换成电压信号的同时完成信号滤波，则形成了跨阻滤波器的设计。跨阻滤波器设计需要知道跨阻滤波器二阶节电路的拓扑结构以及较多的滤波器设计知识[1]。对广大电路设计者而言，电流模式滤波器的设计不如电压模式滤波器设计那样熟悉。所以文中给出一种利用电压模式设计带阻跨阻滤波器的快速实用设计方法，并给出了滤波器的设计实例以及仿真结果。

1 双-T型跨阻带阻滤波器

双-T型网络可以形成陷波，所以被广泛地应用于带阻滤波器设计中，常见的电压模式带阻滤波器电路[2]如图1所示。

为了便于计算， 令 R1=R2=R，C1=C2=C，R3=R/2，C3=2C，可以求得其传递函数为：

给定一组元件值，如： R1=R2=R=2 kΩ，R3=1 kΩ，C1=C2=1 μF，C3=2 μF，R4=R5=1 kΩ。 采用 Spice 进行仿真，得到其波形特性如图2所示。

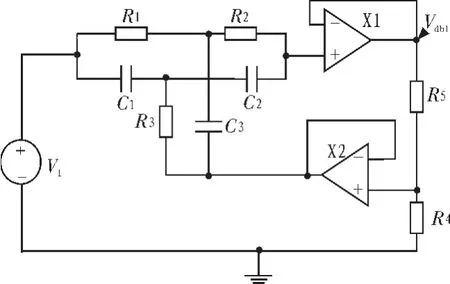
图1 双-T型电压模式带阻滤波器Fig.1 Twin-T voltage mode band-stop filter

图2 双-T型（电压-电压）带阻滤波器特性Fig.2 Twin-T （voltage-voltage）characteristic of band-stop filter

由图2可知，双-T型电压模式带阻滤波器的特性曲线十分理想。在进行跨阻滤波器设计时，如果采用常规设计方法，即将电压源替换为电流源与一个电阻的并联，对原电路进行转换[3]，将得到如3所示的电路图。

图3 常规方法得到的双-T型跨阻带阻滤波器Fig.3 Twin-T trans-impedance filters obtained by the conventional method

其中电路的各元件参数与前面电压-电压型滤波器的参数保持一致，易得其传递函数为：

由上式可得，该系统的低频增益为：

高频增益为：

容易看出 TL（s）≠TH（s），且系统的高频衰减大于低频衰减，当取不同值时，其具体特性曲线如图4所示。

图4 双-T跨阻带阻滤波器的波形失真Fig.4 Distortion of trans-impedance band-stop filter

由图4可知，随着R6阻值的增加，波形的失真衰减程度会加剧[4]，当R6阻值增加到某一足够大的值时，滤波器输出信号中的高频部分就可以被忽略掉，系统将会呈现出低通特性，这就背离了设计带阻滤波器的初衷。显然，这种失真是由R6的存在造成的，但R6又是必需存在的，所以无论怎样调节的R6阻值，都不会彻底消除这种失真的存在。这就需要从电路的拓扑结构特点上入手去分析研究，并找到问题的解决办法。

由前面小节可知，双-T网络之所以有很好的滤波特性，就在于其拓扑结构的对称性。当简单将输入端的电压源替换为电流源与电阻的并联，这样输入端不仅有信号源还引入了一个新的器件--电阻，而这个新引入的电阻器件恰恰影响到了双-T网络的对称性，所以才造成滤波器的低频带与高频带的增益不同。这样要想使跨阻带阻滤波器的波形不失真，就必须减弱或消除R6对双-T网络对称性的影响。研究发现，在运放与双-T网络之间增加一个起隔离作用的运放，可以改善电路的对称性[5]。所以，可以采用在输入端插入单位增益运放的方法来消除波形失真[6]，其电路如图5所示。

图5 双-T型带阻跨阻滤波器Fig.5 Twin-T band-stop trans-impedance filter

其中各器件的参数与之前电路的各器件参数保持一致，即

R1=R2=R，C1=C2=C，R3=R/2，C3=2C，求得其传递函数为：

由上式可知，系统的低频增益为：

高频增益为：

即 TL（s）=TH（s）=R6，所以系统的低频增益和高频增益相同。

给定一组元件值， 如：R1=R2=R=2 kΩ，R3=1 kΩ，C1=C2=1 μF，C3=2 μF，R4=R5=1 kΩ，R6=10 kΩ。采用 Spice 仿真得到的波形如图6所示。

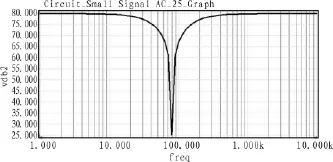
图6 改善后的双-T跨阻带阻滤波器特性Fig.6 Improved Twin-T band-stop trans-impedance filter

由图可以看出，除了系统增益发生变化之外，改善之后的双-T跨阻带阻滤波器与原电压-电压型滤波器具有完全一样的特性曲线。

2 结 论

文中从双-T网络的拓扑结构出发，研究并分析了其良好滤波特性是基于电路的对称性，从而得出，在采用常规方法进行跨阻滤波器转换时，出现波形失真原因是由于破坏了原电路的对称性。于是，为了保持原电路的结构对称性，提出了在输入端插入单位增益运放的设计思路。它在输入端与双-T网络之间起到了隔离的作用，保持了双-T网络的对称性，而且通过调节的阻值，就可以调节整个系统的增益，从而又多了一种对系统参数进行调节的途径，增加了系统设计的灵活性。

此外，通过实际验证，除了双-T网络外，这种采用单位增益运放来进行隔离的方法还适用于其它类型的拓扑网络，因此在进行跨阻滤波器的设计时，可以把它作为一种新的思路。

[1]TAN Ling-ling，LI Qiang，LI Rui-jie，et al.Design of transimpedance low-pass filters[J].International Journal of Electronics，2012（12）：14-16.

[2]Les ThedePractical.Analog and Digital Filter Design[M].Artech House，Inc，2004.

[3]Haigh D G.A method of transformation from symbolic transfer function to active-RC circuit by admittance matrix expansion[J].IEEE Trans.Circuits Syst.I，Reg.Papers，2006，53（12）：2715-2728.

[4]Minaei S.Transimpedance type multifunction filter without using any external passive elements[C]//Proc.25th Midwest Symp.Circuits Syst.（MWCAS），2002：633-636.

[5]Chandra G，Tadeparthy P，Easwaranp.Single amplifier biquadratic filter topologies in transimpedance configuration[J].TEEE Trans.On Circuits and Systems，2008，55（6）：502-506.

[6]Bruton L T.RC-Active Circuits Theovy and Design[M].Prentice Hall，1980.