固体氧化物燃料电池的建模与仿真

吴大中，吴丽华

（南京信息工程大学 江苏省气象探测与信息处理重点实验室，江苏 南京 210044）

固体氧化物燃料电池是一种将气体或者气化燃料的化学能直接转化成电能和热能的一种能量转换装置[1]。SOFC具有清洁、高效、噪音小、无泄漏、无电解质腐蚀、寿命长等优点。燃料的使用具有多样性，既可以用H2作为燃料，也可以利用天然气、CO等其他燃料。近年来，SOFC引起了人们的普遍关注，在许多商业领域也有其应用前景，是目前燃料电池技术中的热点和重点。世界各国研究人员采用电化学、材料学、热力学、流体动力学等相关理论建立了SOFC一些比较完善的数学模型[2-5]。这些模型在研究SOFC的性能的过程中起了很重要的作用，同时，这些模型表达式过于复杂，很难用于控制系统的设计，特别是在线控制[6]。

粒子群（PSO）算法是基于种群搜索的进化类算法，它算法简单、容易编程实现、没有很多参数需要调整、收敛速度较快，因此是一种很有潜力的神经网络学习算法。Van den Bergh F等利用PSO算法对神经网络进行训练，结果性能得到明显改善[7]。径向基函数（RBF）神经网络是一种具有全局收敛的前向网络，它能够以任意精度逼近任一连续函数，并且结构简单、学习速度快，现已被广泛应用于信号处理、模式识别、函数逼近等领域[8]。

结合两者的优点，通过PSO算法对RBF神经网络的中心值进行优化，并调整隐含层到输出层的连接权值，从而为SOFC系统建立更好更精确的模型。仿真结果显示，通过粒子群算法优化RBF神经网络对SOFC系统的建模和控制有一定的实用价值。

1 固体氧化物燃料电池工作原理

SOFC电化学氧化还原反应过程的示意图如图1所示。在阴极，空气中的氧原子与电子发生还原反应，生成氧离子O2-，氧离子O2-在电位差和氧浓度差驱动力的作用下，通过固体电解质离子的导向作用到达阳极。在阳极，燃料气体H2与氧离子进行氧化反应生成水并释放出电子进入外电路，从而产生直流电。电极上的反应式是

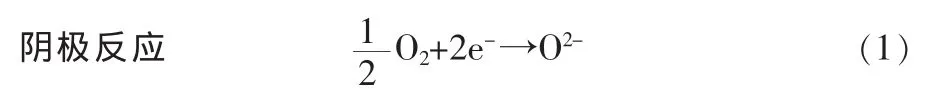
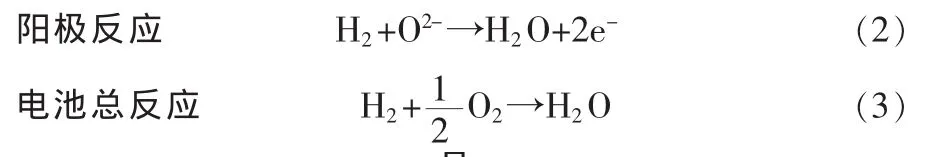
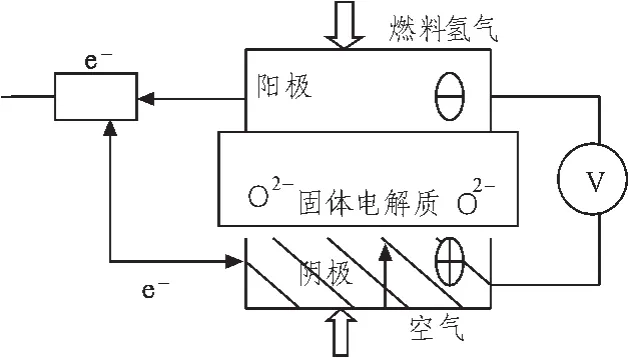
图1 SOFC工作原理图Fig.1 Working principle diagram of SOFC

2 粒子群算法

粒子群算法最早是由Kennedy和Eberhart在1995年提出的。PSO算法源于对鸟类捕食行为的研究，鸟类捕食时，找到食物最简单有效的方法就是搜寻当前距离食物最近的鸟的周围区域[9]。PSO算法就是从这种模型中得到启示并用于解决优化问题的，每个粒子都代表了问题的一个可能解，且都有一个被优化的函数决定的适应度值。粒子还有一个速度决定它们飞翔的方向和距离。为了实现个体在可解空间中的寻优，粒子的速度会随自身及其他粒子的移动经验进行动态调整。

先对可解空间中的粒子进行初始化，粒子的特征用位置、速度和适应度值来表示，空间里的每个粒子都代表一个潜在最优解，适应度值的好坏代表粒子的优劣，其值由适应度函数计算得到。然后粒子通过跟踪个体极值Hbest和群体极值Gbest更新个体位置，个体极值是指该微粒经历过的最优位置，群体极值Gbest是指微粒群中任意个体经历过的最优位置。粒子每更新一次位置，适应度值就相应的进行计算调整，并通过比较个体极值和全局极值来对自身的速度和位置进行更新。

假设微粒群规模为N，搜索空间为D维，每个粒子的位置向量表示为 Xi=（xi1，xi2，…xiD）T，代表问题的一个潜在解。 每个粒子的速度向量为 Vi=（Vi1，Vi2， …ViD）T， 个体极值为 Pi=（Pi1，Pi2，…PiD）T，种群的全局极值为 Pg=（Pg1，Pg2，…PgD）T。 由目标函数即可算出每个粒子Xi位置对应的适应度值。

每一次迭代，粒子都会通过追随两个“极值”来对自己进行更新，更新公式如下:

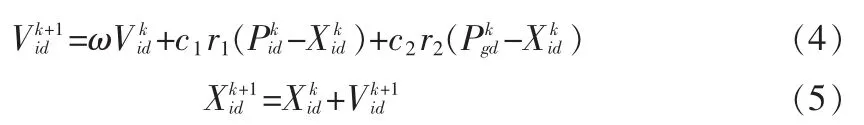
式中，ω为惯性权重，它能使微粒有扩展搜索空间的趋势，有能力探索新的区域，也可以随着迭代线性的减小；d=1，2， …，D；i=1，2， …，n；k 为当前迭代次数；Vid为粒子的速度；c1和 c2是加速度因子，通常在[0，2]之间；r1和 r2为分布于[0，1]之间的随机函数，且相互独立。为了防止在进化过程中，粒子盲目搜索离开空间，通常将Xid和Vid限定于一定范围内[-Xmax，Xmax]、[-Vmax，Vmax]。

3 优化RBF神经网络的PSO算法设计

利用PSO算法训练时，RBF网络中所有需要优化的神经元间的连接权值和中心值，都要先编码成实数码串表示的个体。假设网络中有M个中心值和优化权值，则它们所组成的M维向量就能表示每个个体。依照上述个体结构，产生与微粒群规模相符的一定数量的个体以组成种群，神经网络的不同中心值和权值由不同的个体所代表。同时初始化Gbest、Pbest，就完成了对微粒群的初始化。

然后，对RBF神经网络进行训练。其中神经网络是由群中的每个个体将自己的分量，映射为网络的中心值和权值而形成的。输入训练样本到每个个体对应的神经网络，就能进行训练。为了使神经网络拥有较强的泛化能力，一般将给定的样本空间在训练时分为两部分，用来训练网络的，让网络对训练样本进行学习的，为训练集，另外用来测试样本的，测试已经训练好的网络的性能的那部分，为测试集。在优化过程中，因为要确保每次训练时采用的训练集都不同，所以每次训练时都要对给定的样本集进行分类。为了计算个体的适应度，需要构造如下所示的适应度函数，

其中E（x）为目标函数，即每一个网络在训练集上产生的均方误差，P为训练样本。

对群中的所有个体进行评价来找到最佳个体，看是否有必要更新微粒的Gbest和Pbest。然后，更新所有粒子的速度和位置，产生新的微粒。当均方误差小于给定的ε时，算法终止。

4 基于PSO-RBF的SOFC辨识模型结构

由于SOFC是一个非线性系统，非线性系统常用的简洁模型结构为非线性自回归滑动平均模型（NARX）[10]。

U（k+1）=f[U（k），U（k-1），…，U（k-n），I（k-1），…，I（km），T（k）]（8）

其中，U（k-i）（i=0，1，…n）是系统在 k-i时刻的输出，I（ki）（i=0，1，…m）是系统输入，T（k）是电池温度，f（·）是表征系统特性的待辨识非线性函数。所以本文SOFC的电压/电流密度关系可以用 NARX 来描述。 I（k）、T（k）为输入，U（k+1）为系统实际输出，U^（k+1）为辨识器的输出，ε（k+1）为误差，TDL 为时分多路延时环节[11]。则基于PSO算法的RBF神经网络的SOFC系统辨识的结构框图如图2所示。

5 仿真研究

应用上述算法对SOFC系统进行辨识仿真，根据文献[12]的动态模型采集数据，采集到的数据分为两部分，用于网络训练的为训练集，用于测试已经训练好的网络的性能的为测试集。选择SOFC系统工作温度为T=1 273 K，输入燃料氢气的流量分别为 0.8 mol/s、1 mol/s、1.2 mol/s，图 3 为在氢气、氧气不同流速下，固体氧化物燃料电池电流-电压特性图。

图2 SOFC系统的PSO-RBF辨识模型结构Fig.2 PSO-RBF identification model structure of the SOFC system

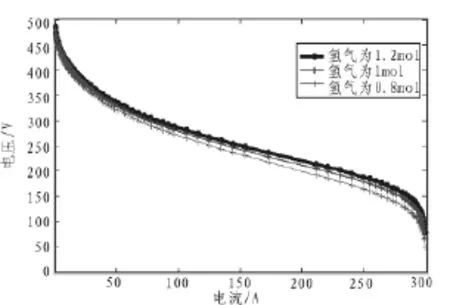
图3 不同氢氧流速下的电流-电压特性Fig.3 I-V characteristics under the different hydrogen and oxygen flow rate

为了说明所建辨识模型的有效性，对模型输入不同的电流密度值，仿真的辨识及逼近误差结果如图4所示。再建立同结构的RBF神经网络模型，输入同样的训练和预测数据，其辨识及逼近误差结果如图5所示。对比图4和图5，可以看出当 I∈[0，20 mA/cm2]时，经过粒子群算法优化的 RBF神经网络比一般的RBF神经网络辨识精度高很多，表明了所建模型的有效性。

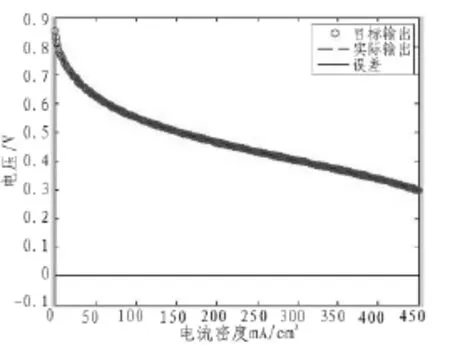
图4 PSO-RBF神经网络辨识及逼近误差图Fig.4 PSO-RBF neural network identification and approximation error chart

6 结 论

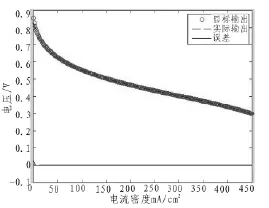
图5 RBF神经网络辨识及逼近误差Fig.5 RBF neural network identification andapproximation error chart

采用PSO算法优化RBF神经网络的中心值和权值，对SOFC系统进行辨识，仿真结果表明此算法精度高，对SOFC电特性模型有很好的辨识作用。说明粒子群算法用于SOFC系统的建模是可行的。另外，粒子群算法容易实现，需要调整的参数少，能很快的计算出结果，从而为实现SOFC系统的在线控制创造了条件。但PSO—RBF模型还需进一步完善，增加变量，把更多的因素纳入考虑范围，建立一个影响因素更为全面的模型，使之有更多的实用价值。

[1]Aguiar P， Adjiman C S， Brandon N P.Anode-supported intermediate temperature direct internal reforming solid oxide fuel cell.I:model-based steady state performance[J].Journal of Power Sources （S0378-7753），2004，138（1-2）:120-136.

[2]Bove R，Lunghi P，Sammes N M.SOFC mathematic model for systems simulations-Part 2:definition of an analytical model[J].International Journal of Hydrogen Energy（S0360-3199），2005，30（2）:189-200.

[3]Nehter P.Two-dimensional transient model of a cascaded micro-tubular solid oxide fuel cell fed with methane[J].Journal of Power Sources （S0378-7753），2006，157 （1）:325-334.

[4]Recknagle K P，Williford R E，Chick L A，et al.Threedimensional thermo-fluid electrochemical modeling of planar SOFC stacks[J].Journal of Power Sources （S0378-7753），2003，113（1）:109-114.

[5]程健，许世森.固体氧化物燃料电池本体模拟研究[J].热力发电，2004，33（12）:13-16.CHENG Jian，XU Shi-sen.Simulation study on the solid oxide fuel cell proper[J].Thermal Power Generation，2004，33（12）：13-16.

[6]吴小娟，朱新坚，曹广益，等.基于神经网络的固体氧化物燃料电池电堆建模[J].系统仿真学报，2008，20（4）:1068-1071.WU Xiao-juan， ZHU Xin-jian， CAO Guang-yi， et al.Modeling solid oxide fuel cell stack based on neural network[J].Journal of System Simulation，2008，20（4）:1068-1071.

[7]Van den bergh F，Engelbrecht A P.Cooperative learning in neural networks using particle swarm optimization[J].South African Computer Journal （S1015-7999），2000，26 （11）:84-90.

[8]刘鑫朝，颜宏文.一种改进的粒子群优化RBF网络学习算法[J].计算机技术与发展，2006，16（2）:185-187.LIU Xin-chao，YAN Hong-wen.A RBF neural network learning algorithm based on improved PSO [J].Computer Technology and Development，2006，16（2）:185-187.

[9]史峰，王小川.MATLAB神经网络30个案例分析[M].北京:北京航空航天大学出版社，2010.

[10]Sjoberg J，Zhang Q H，JUNG L，et al.Nonlinear black-box modeling in system identification:a unified overview[J].Automatica （S0005-1098），1995，31（12）:1691-1724.

[11]霍海娥，霍海波，杨长生.SOFC的支持向量机（SVM）辨识建模[J].系统仿真学报，2010，22（6）:1557-1560.HUO Hai-e， HUO Hai-bo， YANG Chang-sheng.Modeling SOFC based on support vector machine [J].Journal of System Simulation，2010，22（6）:1557-1560.

[12]韩苗苗，沈炯，李益国.固体氧化物燃料电池的多模型预测控制方法研究[J].华东电力，2009，37（10）:1767-1770.HAN Miao-miao， SHEN Jiong， LI Li-guo.Multi-model predictive control of solid oxide fuel cells[J].East China Electric Power，2009，37（10）:1767-1770.