基于信息学理论的基因数据挖掘研究
昂清,王卫东,王国静,彭福来
1 解放军总医院医学工程保障中心生物医学工程研究室,北京市,100853
2 北京理工大学信息与电子学院,北京市,100081
0 引言
2001年2月12日,美国Celera公司与人类基因组分别在《科学》[1]和《自然》[2]杂志上公布了人类基因组精细图谱及其初步分析结果。两个不同的组织使用不同的方法实现了共同的目标:完成对整个人类基因组的测序工作,并且两者的结果惊人的相似。整个人类基因组测序工作的基本完成,为人类生命科学开辟了一个新纪元。它对生命本质、人类进化、生物遗传、个体差异、发病机制、疾病防治、新药开发、健康长寿等领域,以及对整个生物学都具有深远的影响和重大意义,标志着人类生命科学一个新时代的来临。
人类基因组测序计划[3]完成后,国内外学术界掀起了如火如荼的基因组学研究。这表明人类探索自身的进程由数据采集发展到了数据分析和挖掘的新阶段,标志着现代医学基础和临床研究正在逐步走向纵深。
随着数据采集的新理论、新技术和新设备的不断涌现,原始基因数据的维数不断增加,随之而来的就是数据处理和分析方面的问题。为了切实提高基因数据处理的效率,增加数据挖掘结果对疾病早期预警、诊断和个体化治疗方案制定的有效性[4],基因数据特征选择和挖掘方法的确定就显得至关重要。以往的研究大多是在对原始数据进行简单预处理后,仅从统计学[5]、人工智能[6-7]或机器学习[8]的单一角度出发开展研究。本文在参阅大量文献资料的基础上,提出了基于信息学理论的特征选择方法,同时利用流形学习理论中非线性降维ISOMAP算法建立数学模型,初步实现了基于基因数据的疾病智能分类研究。
1 基因数据的特点
基因数据是一种较为常见的临床医学数据类型。由于医学数据采集仪器和设备的快速发展,导致基因数据量和维数的大幅增加。但因各种主客观原因,例如仪器设备的精度、人为因素等的影响,数据中存在着一定的误差、错误甚至冗余。
误差在一定的精度范围内难以避免,错误则可以通过修正加以改正,而冗余问题则较难避免或修正。冗余的存在,不仅会降低数据处理的效率,而且会对处理结果产生一些影响,甚至会导致其偏离研究的目标。由于版面限制,下图1仅显示了部分原始淋巴瘤基因数据[9]。

图1 部分原始基因数据(淋巴瘤)Fig.1 Part of raw gene data (lymphoma)
为了提高处理效率和增加处理结果的可解释性,迫切需要在现有研究方法的基础上,根据基因数据的特点设计适合的处理和分析方法。
2 基因数据处理的基本流程
作为知识发现(KDD, Knowledge Discovery in Databases)的重要组成部分,依照数据挖掘的一般过程,基因数据挖掘也可以大致分为以下几个基本步骤,如图2所示。

图2 基因数据挖掘基本流程Fig.2 Basic flow of gene data mining
对原始数据进行预处理,就是为了清洗、完善、补全甚至归一化数据,从而为后续的数据挖掘铺平道路。在本研究中,将基因的表达离散化为三个状态,用-1、0、1来表示。

图3 预处理后的基因数据(淋巴瘤)Fig.3.Preprocessing data of raw gene (lymphoma)
高维是基因数据的基本特点之一,但这并不意味着所有数据都是有效的,有很大一部分基因数据对于疾病分类和诊断来说是无效的,因此在开展研究时需要剔除这部分数据,以降低计算量和难度。特征选择可以实现高维数据向低维数据的转变,它其实是预处理的一个重要步骤,将其单列出来就是为了强调它的重要性。通过选择适当的特征子集,剔除冗余的基因特征,在降低分析和处理的计算量和难度的同时,利于发现与疾病早期预警和诊断高度相关的特异性基因表达,因此开展基因特征选择是非常必要的。
3 基于信息学理论的基因特征选择方法
信息学理论的概念和方法,在信号处理与分析的众多领域发挥着举足轻重的作用,将其应用于基因数据的挖掘研究,必将推动信息学与医学的融合与共同发展。
运用信息学理论来理解基因间的关系:若两个基因高度相关,当其中一个基因与疾病分类有强联系时,另一个必然与疾病分类存在强联系;在特征子集选择时就要避免同时选择这两个基因,否则在子集维数一定情况下会导致有效维数的减少。因此,开展特征选择时,应使子集中的特征基因间尽可能地不相关,即以冗余最小化来提高特征子集的有效性。选择互信息作为衡量基因间冗余程度的参数进行定量计算,互信息最小意味着所选择的子集在特征数目一定的情况下能够更全面地代表整个数据集。对于离散数据,计算公式如下:

其中:S代表所选择的基因特征子集,m是特征子集中特征基因的个数,I(gi,gj)代表第i个基因与第j个基因的互信息。I(gi,gj)可用公式(2)来进行计算:
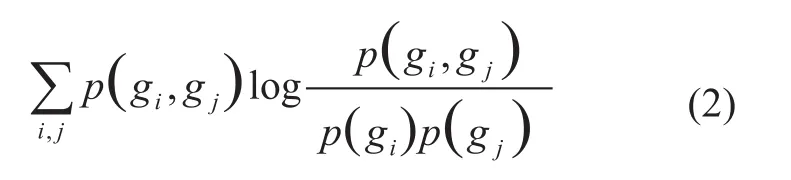
当一个基因在不同类型或亚型的疾病间表达特异性越高时,则其与疾病的相关性越大,找到了这个基因就能从一定程度上判断疾病的状态,这个基因在某种程度上可以被称为疾病的标记。因此,选择特征子集时,需要尽可能地选择与疾病相关性最大的基因。运用信息学理论来定量计算基因与疾病间的相关性:

其中:S与和m公式(1)中含义相同,h代表类别变量即疾病的类型,I(gi,h)表示第i个基因与类别变量h的互信息。
当公式(1)和公式(3)同时满足时,所获得的子集即为本研究所选择的特征子集。为了简化判别条件,假定公式(1)与公式(3)在特征选择时所占的影响比重相等,合并后得到公式(4):

其中,Ω代表整个基因数据集,ΩS代表原始数据集选出特征子集Ω后剩余的子集。
文献[10]认为:特征基因的选择方法,可按照基因在不同表现型中的特异表达对其进行排序,并且选择排在前面的50个基因作为特征基因。大量特征选择实践表明,在特征数目的确定方面没有明确或公式可依的定量方法,尽管有少量研究表明根据数据分布的特点可以设置特征的数目,但到目前为止主要还是依靠经验、直觉进行判断,绝大部分原因在于难以把握原始数据的分布特点。本研究将在实验结果部分显示不同数目特征基因的建模分析结果。
4 流形学习方法简介
流形(Manifold)的概念源自拓扑学,它表示一个局部处为欧几里德的拓扑空间[11]。局部具有欧式空间特性意味着对于空间上任一点都有一个邻域,在这个邻域中的拓扑空间与m维欧式空间中的开放单位圆相同,即流形是一个局部可解析的拓扑空间。
流形学习(Manifold Learning)的基本思想是:假设数据是均匀采样于一个高维欧式空间中的低维流形,流形学习就是从高维采样数据中恢复低维流形结构,并求出相应的嵌入映射,以实现降维或者数据可视化。它是从观测数据中寻找事物的本质,挖掘其内在的规律,与医学数据挖掘的目的相一致。
测地线(Geodesic)是流形中一个很重要的概念,它起源于大地测量学(Geodesy),被定义为空间中两点的局域最短路径。在测地线概念的基础上,研究者发展了多种流形学习算法,Tenenbaum等人提出的ISOMAP算法[12]就是其中的一种。ISOMAP算法首先使用最近邻图中的最短路径得到近似的测地线距离,代替不能表示内在流形结构的欧式距离,然后输入多维尺度分析(MDS, Multidimensional Scaling)中进行处理。其目的在于发现嵌入在高维数据集的内在低维结构,属于非线性降维范畴,已经在图像处理如人脸图像、手写数字图像等方面得到了应用。
具体的ISOMAP计算步骤如下:
1)计算每个点的近邻点 (用k近邻或 口 邻域);
2)在样本集上定义一个赋权无向图,如果Xi和Xj互为近邻点,则边的权值为dX(i,j);
3)计算图中两点间的最短距离,记所得的距离矩阵为DG= {dG(i,j)} ;
4)用MDS求低维嵌入流形,代价函数:

低维嵌入是τ(D)的第2小到第 d+1小的特征值所对应的特征向量。
本文在对原始基因数据进行特征选择的基础上,选用流形学习方法进行建模研究。
5 实验结果及分析
实验原始数据:淋巴瘤数据来自Alizadeh et al[9],96*4026,共96位患者,9个疾病亚类;来自NCI(National Cancer Institute, 美国国家癌症研究院)的Ross et al[13]和Scherf et al[14],60*9703,共60位患者,9个疾病亚类;肺癌数据来自该院的Garber et al[15],73*918,共73位患者,7个疾病亚类;白血病数据来自该院的Golub et al[10],72*7070,72位患者,2个疾病亚类;结肠癌数据来自该院的Alon et al[16],62*2000,62个采样样本,分为肿瘤和正常两类。
下图4-8分别显示5个原始基因数据集在经过特征选择和流形学习的建模过程后,不同特征数目情况下所显示的低维流形。通过对比分析发现:在原始数据维数远远大于特征数目的情况下,从m=50开始就逐渐显示出流形学习的分类特性,间接证明了文献[10]的特征数目确定理论;但是随着特征数目的增加,又会出现疾病类别合并的现象。

图4 淋巴瘤数据在不同数目特征基因的情况下的流形分析结果图Fig.4.Manifold learning results of lymphoma under different number of characteristics

图5 NCI数据在不同数目特征基因的情况下的流形分析结果图Fig.5 Manifold learning results of nci under different number of characteristics
6 讨论与结论
通过本研究设计的系统模型对基因数据进行处理和分析,能够在降低计算量和提高疾病分类准确度方面获得进展,但是在以下几个方面仍存在可改进和完善之处:

图6 肺癌数据在不同数目特征基因的情况下的流形分析结果图Fig.6.Manifold learning results of lung under different number of characteristics

图7 白血病数据在不同数目特征基因的情况下的流形分析结果图Fig.7.Manifold learning results of leukemia under different number of characteristics

图8 结肠癌数据在不同数目特征基因的情况下的流形分析结果图Fig.8.Manifold learning results of colon under different number of characteristics
1) 在特征选择的条件约束制定方面,本文中假设公式(1)和公式(3)对选择的影响比重相等,但实际情况未必如此。因此,后续的研究将引入一个影响比重变量,根据建模结果进行反馈调节,以期发现更为合适的比重因子。
2) 从本质上说,ISOMAP方法适合于处理内部平坦的低维流形,不适于学习有较大内在曲率的流形。因此,在原始基因数据内部结构是否平坦这一问题未知的情况下,开展研究存在一定的风险。随着噪声的增大,ISOMAP算法的可视化出现不稳定现象,即低维流形中不同邻域的数据点在投影后出现混杂现象。后续研究将改进这一方法,使模型具有更强的普适性,从而能够适用于更广泛的医学数据分析和处理问题。
总体说来,本文所设计的系统模型在基因数据分析和处理方面,具有一定的实用性和有效性,但其精确度和可解释性仍有待进一步提高。
[1]Venter, J.C, Adams, M.D, Myers, E.et al.The sequence of the human genome[J].Science, 2001, 291(5507): 1304-1351.
[2]International Human Genome Sequencing Consortium.Initial sequencing and analysis of the human genome[J].Nature, 2001,409(6822): 860-921.
[3]余国鹰.人类基因组测序草图完成十年[J].中国心脏起搏与心电生理杂志, 2010, 24(3): 269.
[4]昂清, 王卫东.生物标记物的数据挖掘在临床医学中的研究[J].科学技术与工程, 2007, 7(6): 1237-1239, 1247.
[5]Wei Zhang, Ilya Shmulevich.Computational and statistical approaches to genomics[M].kluwer academic publishers, norwell,Massachusetts 02061 USA, 2002
[6]陈志宏, 严壮.人工神经网络在基因组信息学中的应用[J].国外医学(生物医学工程分册), 2002, 25(4): 145-149.
[7]昂清, 王卫东.自组织特征映射在人群健康风险评估中的应用研究[J].科学技术与工程, 2007, 7(9):2037-2041, 2057.
[8]詹超, 胡江洪.SVM在基因表达数据分类中的研究与应用[J].计算机技术与发展, 2006, 16(3): 107-109.
[9]Alizadeh AA, Eisen MB, Vavis Re, et al.Distinct types of diffuse large B-cell lymphoma identified by gene expression profiling[J].Nature, 2000, 403(6769): 503-511.
[10]Golub TR, Slonim DK, Tainayo P, et al.Molecular classification of cancer: class discovery and class prediction by gene expression monitoring[J].Science,1999, 286(5439): 531-537.
[11]徐蓉, 姜峰, 姚鸿勋.流形学习概述[J].智能系统学报, 2006, 1(1):44-51.
[12]Tenenbaum JB, de Silva V, Langford JC.A global geometric framework for nonlinear dimensionality reduction.Science, 2000,290 (5500): 2319-2323.
[13]Ross DT, Scherf U, Eisen MB, et al.Systematic variation in gene expression patterns in human cancer cell lines[J].Nat Genet 2000,24(3): 227-235.
[14]Scherf, U, Ross, D.T, Waltham M.et al.A cDNA microarray gene expression database for the molecular pharmacology of cancer[J].Nat Genet, 2000, 24(3): 236-244.
[15]Garber ME, Troyanskaya OG, Schluers K.et al.Diversity of gene expression in adenocarcinoma of the lung[J].PNAS USA,2001,98(24):13784-13789.
[16]Alon U, Barkai N, Notterman DA, et al.Broad patterns of gene expression revealed by clustering analysis of tumor and normal colon tissue probed by oligonucleotide arrays[J].PNAS USA,1999, 96(12): 6745-6750.

