本征值问题的修正傅里叶级数解
李红艳, 万钟林
(1. 东莞理工学院 城市学院 计算机与信息科学系, 广东 东莞, 523106; 2. 东莞职业技术学院 财经系, 广东 东莞, 523808)
本征值问题的修正傅里叶级数解
李红艳1, 万钟林2
(1. 东莞理工学院 城市学院 计算机与信息科学系, 广东 东莞, 523106; 2. 东莞职业技术学院 财经系, 广东 东莞, 523808)
为了使本征值问题的求解更加完善, 利用Iserles在2008年提出的修正傅里叶级数的三角基函数, 使数学物理方法中的分离变量法成为一个全新的求解方法. 利用这一方法对一类定解问题进行求解, 最终得到了该问题的修正傅里叶级数解, 验证了所提出的新方法的正确性.
偏微分方程; 分离变量法; 级数解
对于偏微分方程的求解方法, 前人已经提出很多严密的理论. 法国数学家傅里叶提出的傅里叶级数极大地推动了偏微分方程理论的发展. 而傅里叶级数法作为求解定解问题的经典理论已经得到了广泛的应用.而由Iserles在2008年提出的修正傅里叶级数更丰富了前人的理论. 下面通过修正傅里叶级数的三角基函数求解一类定解问题.
数学物理问题中有这样一类定解问题[1]:
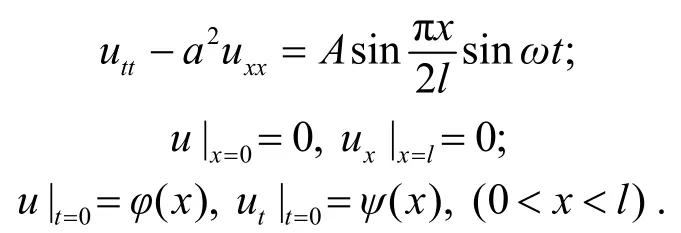
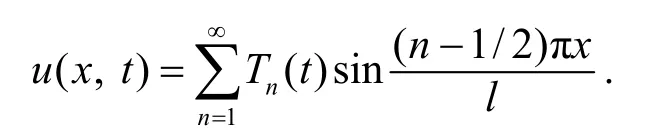

左边是修正的傅立叶正弦级数, 这提示我们把右边也展开为修正的傅立叶正弦级数. 其实, 右边已经是修正的傅立叶正弦级数了, 它只有一个单项即n=1的项. 于是, 比较两边的系数, 分离出的常微分方程:
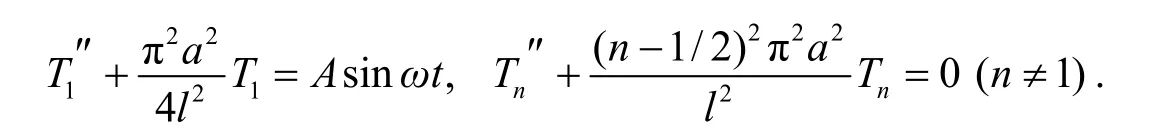
又把u( x, t)的修正傅立叶正弦级数代入初始条件, 得:

其中, φn、ψn分别为φ( x)和ψ( x)的修正傅立叶正弦级数[以sin[(n-1/2)πx/ l]为基本函数族]的第n个修正傅立叶系数. 等式(1)、(2)两边都是修正傅立叶正弦级数. 由于基本函数族的正交性, 等式两边对应同一基本函数的修正傅立叶系数必然相等, 于是得Tn( t)的非零值初始条件:

Tn( t)的常微分方程在初始条件(3)下的解是:
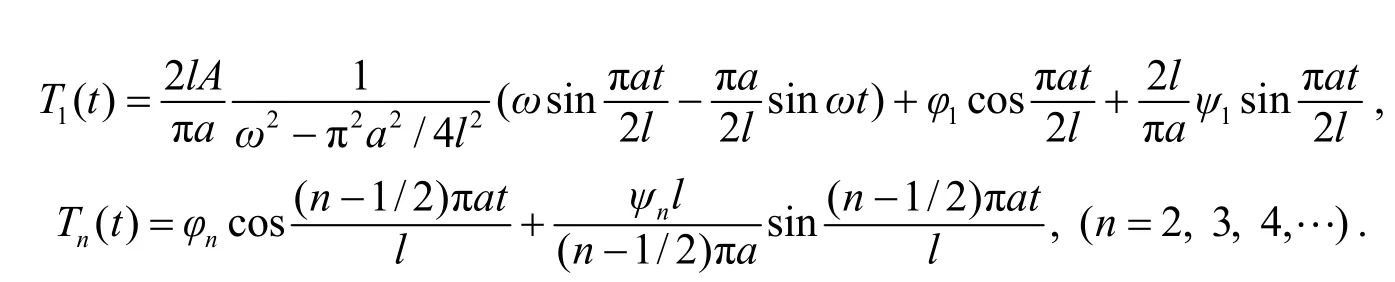
这样, 所求得的解是:

可见, 用修正的傅立叶级数法求解这个定解问题相当成功. 很明显, 这个方法的关键在于分离出Tn( t)的常微分方程, 其中不可混杂着另一自变量x, 这是怎么做到的呢?原来, 这个级数展开的基本函数sin[(n-1/2)πx/l]正是相应齐次方程、齐次边界条件下用分离变量法求得的本征函数, 这才得以分离出Tn( t)的常微分方程.
[1] 梁昆淼. 数学物理方法[M]. 北京: 高等教育出版社, 1998.
[2] Iserles A, Nørsett S P. From high oscillation to rapid approximation I: Modified Fourier expansions[J]. IMA J Num Anal, 2008, 28: 862-887.
(责任编校: 刘晓霞)
Modified Fourier series solution of the eigen-value problem
LI Hong-yan1, WAN Zhong-lin2
(1. Department of Computer Science and Technology, City College, Dongguan Institute of Technology, Dongguan 523106, China; 2. Finance Department, Dongguan Vocational and Technical College, Dongguan 523808, China)
In order to solve the eigenvalue problem, a new method was proposed, one of the separation of variables in the mathematical physics based by the modified triangle basis functions suggested by Iserles in 2008. And then a class of problems was solved using this new method. And a right solve for this problem was put forward, which was verified the correctness of the proposed new method.
partial differential equations; separation of variables method; series solution
O 173.1
1672-6146(2012)02-0004-02
10.3969/j.issn.1672-6146.2012.02.002
2012-04-20
李红艳(1984-), 女, 硕士生, 主要从事数值代数、反问题的研究. E-mail: 271665792@qq.com

