改进的Prony算法提取舒曼谐振参数

周洪娟，于海雁，乔晓林

(哈尔滨工业大学(威海)信息工程研究所，264209 山东威海)

改进的Prony算法提取舒曼谐振参数

周洪娟，于海雁，乔晓林

(哈尔滨工业大学(威海)信息工程研究所，264209 山东威海)

为在更短的时间内提取舒曼谐振参数，引入对时域采样数据进行直接处理的Prony算法.针对该算法受噪声影响大的缺点，对算法的核心过程——超定方程的求解方法进行了改进，采用Martin等人提出的最小残数法，并与频域处理结果进行对比分析，验证该算法的有效性.

舒曼谐振;Prony算法;非线性最小平方拟合;谐振频率;最小残数法

舒曼谐振(SR)是由全球闪电活动激励在地-电离层腔中固定存在的一种谐振现象，各阶谐振波长与地球周长成比例，前四阶谐振频率近似为8、14、20和26 Hz，舒曼谐振各阶参数的研究对全球闪电活动、气温的微弱变化以及大气层和电离层参数的变化具有重要意义［1－5］，另外，最近也有关于 SR与地震关系的研究［6－7］.但传感器在接收低频环境磁场数据过程中，通常会受到其他干扰和噪声的影响，如人类在周围空间的活动、近处的雷暴活动以及强烈的地壳运动等，都会使得测量的背景噪声增强，从而淹没极其微弱的舒曼谐振信号.当然，这些干扰因素是不可避免的，我们能做的就是选择远离工业区的偏远地方作为观测站，以及采用抗干扰和噪声比较好的算法来提取舒曼谐振特征参数.

对舒曼谐振参数的提取，最常规的方法就是在频域上处理，但对于信噪比很低的观测数据往往要进行长时间的积累平滑以得到比较清晰的频谱图，这对于一些持续时间比较短的突发自然现象的研究，如太阳耀斑、磁暴等对SR参数的影响的研究是不利的.本文引入基于时域采样数据的谐波估计算法——Prony算法，该算法在电力系统谐波和间谐波的检测方面应用比较多［8－10］，可以在较短的时间内提取谐波参数，但是经典Prony算法的谐波估计性能受噪声影响较大.本文首先对Prony算法在低信噪比数据中的应用进行讨论，并提出改进算法，以位于云南某观测站的低频磁场数据为例，分别在频域和时域估计舒曼谐振的参数，再进行对比分析，得到比较可靠的舒曼谐振参数时域估计方法.

1 数据说明

观测站位于比较偏远的云南山区，主要观测ELF频段环境磁场数据，观测带宽40 Hz左右，采样率为100 Hz.观测数据中的干扰和噪声很多，舒曼谐振信号是淹没在这些干扰和噪声之下的，图1(a)为10 s的采样数据，数据中噪声污染严重，对应的频谱如图1(b)蓝线所示，几乎看不出SR的轮廓，这通常需要一段时间的积累才能得到比较清晰的频谱，图1(b)红线为10 min的数据做傅里叶变换后的平均频谱，频率分辨率为0.1 Hz，可明显看到前四阶舒曼谐振信号的轮廓，谐振频率分别在8、14、20和26 Hz左右，但频谱数据极不平滑，不利于对舒曼谐振参数的进一步提取与分析.

2 Prony算法分析

2.1 算法简介

Prony算法是用复指数函数的线性组合来描述等间距采样数据的一种数学方法，从而根据采样数据直接估计出信号的频率、衰减、幅值和初相位.对实数采样数据，算法的主要思想如下:设时域信号为一系列存在衰减的正弦信号之和，由三角函数的变换，可以写成一系列复指数函数之和，如下式所示:

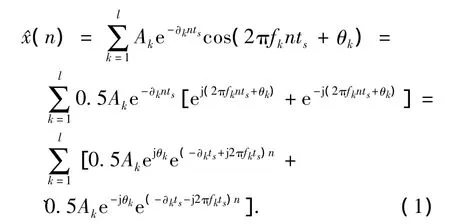
进一步，令

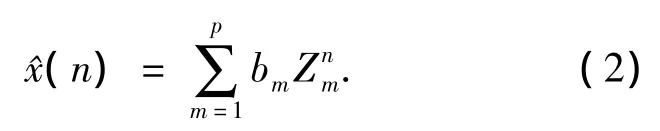
其中:p=2l为估计的复指数函数阶数;bm=Amejθm或 bm= Ame-jθm， 互 为 共 轭 对;Zm=e-∂mts+j2πfmts或 Zm=e-∂mts-j2πfmts，也是互为共轭对.

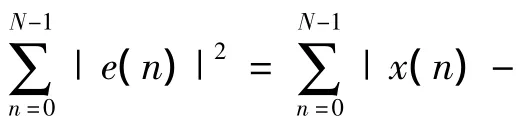
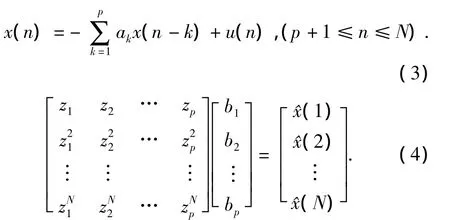
2.2 算法改进

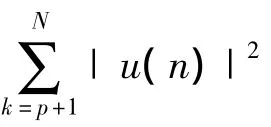
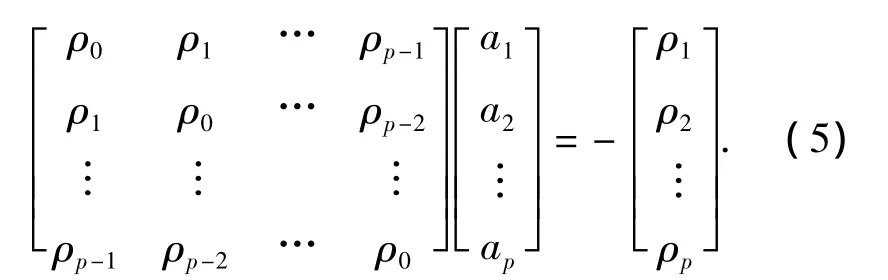
对任意超定方程如下所示:

其中:G∈Rm×n，且m ＞ n;a ∈Rn，y∈Rn.式(5)的过程相当于对式(6)求最小平方和估计，即有

为了避免ρ0项的影响，Martin等人采用如下的方法，称为最小残数法［12］:即构造矩阵G的子集G1，同时取对应向量y的子集y1，有G1a=y1，两边同乘以1个矩阵，有

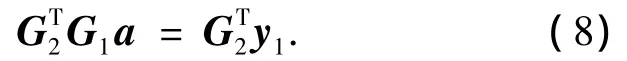
其中G2也为矩阵G的子集，同时要确保矩阵G1中不包含ρ0项.

按照这一思路，任取1个值n，使其满足p+1≤n≤N-p，将式(3)写成式(6)的标准矩阵形式，取

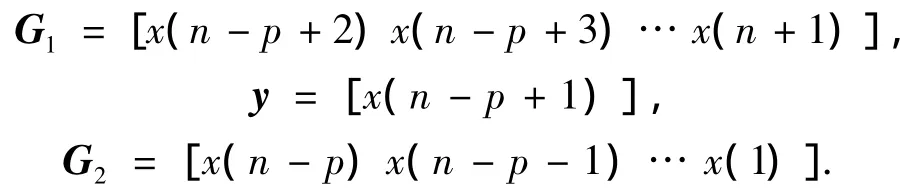
按照式(8)可以构造如下的关系式:

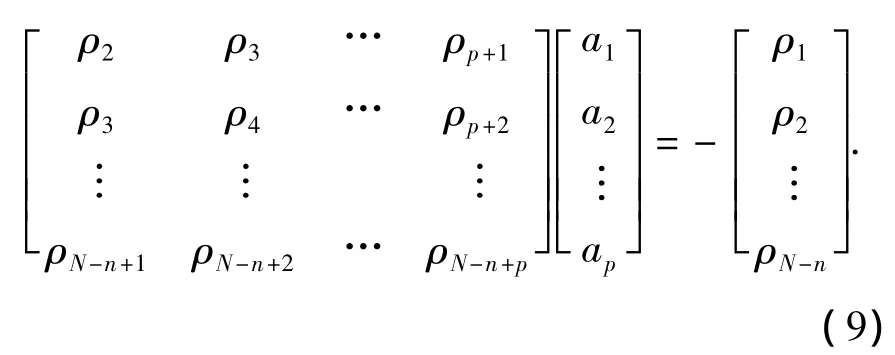
可见式(9)与式(5)相比，避免了部分噪声的影响.

2.3 算法仿真

采用3个频率分别为8、14和20 Hz的衰减信号之和为例，再加入一定的噪声，分析噪声对基于式(5)和式(9)的Prony算法的影响.采样率设为100 Hz，分析时长为1 s.

图2中实线、带点实线和带星号实线分别表示未加噪声σ=0、加入噪声σ=0.2和σ=0.6三种情况下，按照式(5)和式(7)的传统Prony算法估计出的信号波形以及频谱图，估计出的参数见表1，其中估计阶数均定为p=10.可见传统的Prony方法对理想的信号估计精度很高，但对噪声非常敏感，更不适用于SR信号的处理.而表2为同样的测试数据采用式(9)估计出的参数，明显发现该算法性能优于传统的Prony方法，尤其是对衰减因子估计性能的改善.

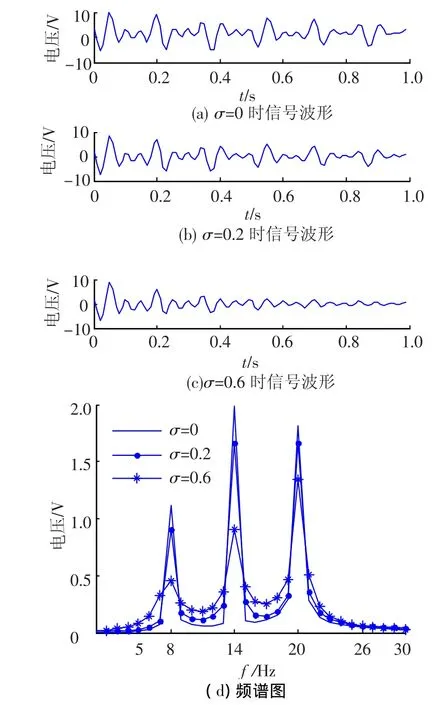
图2 传统Prony算法在不同的噪声污染情况下恢复的信号波形和频谱图

表1 基于传统的Prony算法估计结果

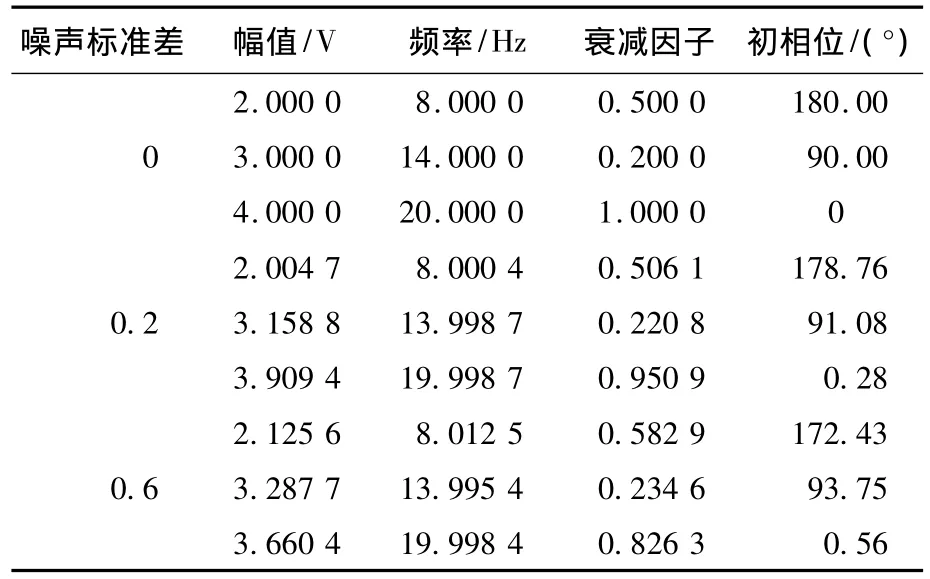
表2 基于改进算法的Prony算法估计结果

3 SR特征参数提取

SR参数包含各阶的中心频率、幅度、以及带宽等.本节首先采用频域方法对SR参数进行提取，以此验证Prony算法的有效性.

3.1 频域提取

对图1(b)的频谱采用非线性最小平方拟合方法进行拟合，拟合后的曲线如图3红色粗线所示，蓝色曲线为拟合前的曲线，前四阶舒曼谐振的中心频率和幅度如表3所示.这种方法估计结果比较准确，但时间分辨率比较低，在一些特殊的分析中，如太阳耀斑时引发的SR频率的短暂变化等应用中会有局限性.

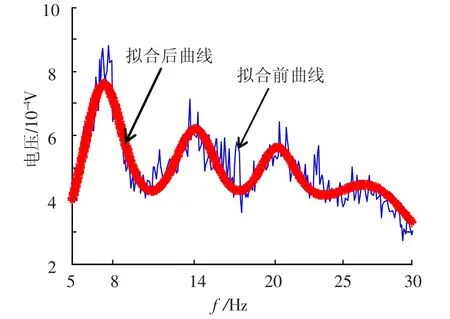
图3 拟合后的SR频谱图

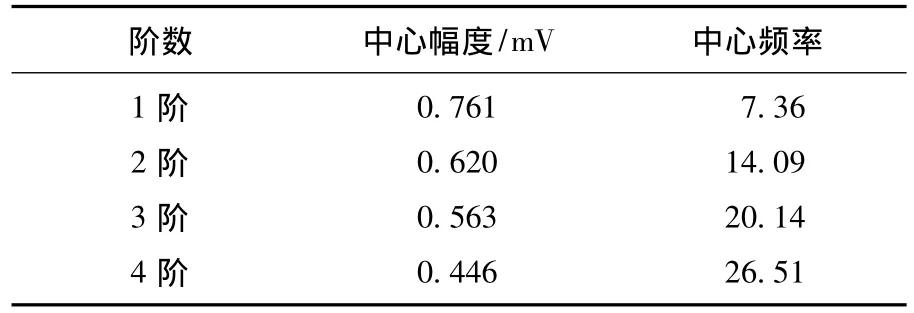
表3 基于频域方法提取的SR参数

3.2 时域提取

Prony算法的估计阶数采用基于奇异值分解的阶数确定方法［13］，对噪声的有效抑制采用式(9)的方法.通常情况下，若对波形进行估计，Prony算法一次参与计算的数据点数不能太多，因为随着时间的增大，衰减因子和频率估计的误差就会被逐渐放大，而使得估计波形的误差越来越大，尤其对干扰比较严重的数据，这种情况更明显［14］.因为波形本身并不被关心，而是希望得到比较准确的参数估计，因此本文采用20 s数据为一处理时长，对图1(b)的10 min平滑频谱对应的数据进行分段Prony谐波估计，得到前两阶谐振的频率变化如图4所示.

其中红线代表30个估计值的平均值，对应前两阶SR的平均值分别为7.359 1 Hz和13.991 6 Hz，与频域估计值基本吻合，但存在差别，主要因为观测数据的噪声污染很严重.Prony算法虽然估计性能会受到噪声的影响，但估计的时间分辨率可以很高，要得到比较稳定的估计值，下一步还需要对估计阶数采用更灵活的确定方法，采用抗噪声能力更强的算法.

图4 采用Prony算法估计的SR前两阶频率

4 结论

本文利用扩展的Prony算法对信噪比接近0 dB的SR观测数据进行参数估计，采用了Martin等人对含有噪声的超定方程的求解思路，避免了超定方程系数矩阵中的自相关函数项，提高了Prony算法的抗噪声性能.实际测试表明，这种方法估计出的SR频率与频域方法的结论基本吻合.但是，为了得到Prony算法对SR观测数据的稳定估计，还需要做进一步的研究，包括对数据的预处理、估计阶数的自适应选择以及更鲁棒的抗噪声算法等.

［1］SHVETS A V，HPBARA Y，HAYALAWA M.Variations of the global lightning distribution revealed from three-station schumann resonance measurements［J］.Journal of Geophysical Research，2010，115(A12)，doi:10.1029/2010JA015851.

［2］DE S S，DE B K，BANDYOPADHYAY B，et al.Studies on the shift in the frequency of the first Schumann resonance mode during a solar proton event［J］.Journal of Atmospheric and Solar-Terrestrial Physics，2010，72(11/12):829－836.

［3］WILLIAM E R，SATORI G.Solar radiation-induced changes in ionospheric height and the Schumann resonance waveguide on different timescales［J］.Radio Science，2007，42(RS2S11)，doi:10.1029/2006RS003494.

［4］ROLDUGIN V C，MALTSEV Y P，VASILJEV A N，et al.Changes of schumann resonance parameters during the solar proton event of 14 July 2000［J］.Journal of Geophysical Research，2003，108(A3)，doi:10.1029/2002JA009495.

［5］SIMOES F，GRARD R，HAMELIN M，et al.The schumann resonance:a tool for exploring the atmospheric environment and the subsurface of the planets and their satellites［J］.Icarus，2008，194(1):30 － 41.

［6］OHTA K，WATANABE N，HAYAKAWA M.Survey of anomalous schumann resonance phenomena observed in Japan，in possible association with earthquakes in Taiwan［J］.Physics and Chemistry of the Earth，2006，31(4/5/6/7/8/9):397－402.

［7］OHTA K，IZUTSU J，HAYAKAWA M.Anomalous excitation of schumann resonances and additional anomalous resonances before the 2004 mid-niigata prefecture earthquake and the 2007 Noto Hantou earthquake［J］.Physics and Chemistry of the Earth，2008，34(6/7):441 －448.

［8］沈杨，戴本祁，张惠东.基于小波和扩展Prony算法的电压闪变检测新方法［J］.电力系统保护与控制，2010，38(10):43 －47.

［9］ZYGARLICKI J，ZYGARLICKA M，MROCZKA J，et al.A reduced Prony’s method in power-quality analysis-parameters selection［J］.IEEE Transactions on Power Delivery，2010，25(2):979 －986.

［10］CHEN C I，CHANG G W.An effective time-domain approach based on Prony’s method for time-varying power system harmonics estimation［J］.Power and Energy Society General Meeting，2009(7):1 －6.

［11］张贤达.现代信号处理［M］.北京:清华大学出版社，2002:119－126.

［12］FULLEKRUG M.On the minimization of correlated residuals［J］.Geophysical Journal International，1996，126(1):63－68.

［13］熊俊杰，邢卫荣，万秋兰.Prony算法的低频振荡主导模式辨识［J］.东南大学学报(自然科学版)，2008，38(1):64－68.

［14］董航，刘涤尘，邹江峰.基于Prony算法的电力系统低频振荡分析［J］.高电压技术，2006，32(6):97－100.

Improved prony algorithm for abstracting schumann resonance parameters

ZHOU Hong-juan，YU Hai-yan，QIAO Xiao-lin

(Institute of Information Engineering，Harbin Institute of Technology at Weihai，264209 Weihai Shandong，China)

In order to abstract Schumann Resonance parameters in shorter time，Prony algorithm is adopted and analyzed here to process the sampling data directly without FFT.Due to the fact that the algorithm is noise-sensitive，the minimization of correlated residuals proposed by Martin is adopted for solving the overdetermined equations and verified with simulated signals.It is proved to be feasible for SR signal processing after compared with the results from frequency domain.

schumann resonance;prony algorithm;non-linear least-square fit;resonance frequency;minimization of correlated residuals

TN911.72

A

0367－6234(2012)07－0083－04

2011－04－12.

山东省自然科学基金资助项目(ZR2010DM013);科技部中日合作基金资助项目(2012DFG20510).

周洪娟(1980—)，女，讲师;

乔晓林(1948—)，男，教授，博士生导师.

周洪娟，hongjue_zhou@sina.com.

(编辑 张 宏)