不确定条件下民航发动机维修工作范围决策

付旭云，崔智全，钟诗胜

(哈尔滨工业大学(威海)机械工程系，264209 山东威海)

不确定条件下民航发动机维修工作范围决策

付旭云，崔智全，钟诗胜

(哈尔滨工业大学(威海)机械工程系，264209 山东威海)

为降低民航发动机维修成本和提高修后性能，提出不确定条件下的发动机维修工作范围决策方法.将发动机各单元体各维修级别能够恢复的整机性能值表示为一个梯形模糊数，建立单元体性能恢复值分配优化的模糊机会约束规划模型;将模型的机会约束转化为清晰等价类，发现该模型和确定条件下的单元体性能恢复值分配优化模型具有相同的结构，能够采用确定条件下模型的求解方法进行求解;利用应用实例对提出方法进行了验证.结果表明:提出方法能够解决不确定条件下的发动机维修工作范围决策问题;模型机会约束的置信水平对决策结果至关重要，要综合考虑实现送修目标的风险和维修成本，确定合理的置信水平.关键词:航空发动机;单元体;维修工作范围;排气温度裕度;性能恢复值

为了保障民航发动机的适航性，在其全生命周期内，必须持续进行维护、维修和大修等工作.发动机送入承修厂进行修理时，首先需要确定做什么修理工作，即确定维修工作范围.维修工作范围影响着发动机的维修成本以及修后可靠性和性能;因此，合理确定发动机维修工作范围对于航空公司具有重要意义.现代民航发动机结构复杂，广泛采用定时维修、视情维修和状态监控3种方式相结合的维修策略［1］，其维修工作范围制定的影响因素众多，一般设备的维修工作范围决策方法［2］不适用.现代民航发动机大都由单元体组成［3］，所以确定发动机维修工作范围就转化为确定各个单元体的维修工作范围了.对每个单元体，发动机供应商都会给出几个标准的维修工作范围，称为维修级别，确定发动机维修工作范围也就是确定各单元体的维修级别.

目前，国内外主要采用如下3种方法进行发动机维修工作范围的决策.1)遍历方法［4－5］.该方法对发动机所有可能的维修工作范围进行评估，根据评估结果选择合适的维修工作范围.该方法存在的主要问题是效率较低，不适应于工程应用.2)基于规则的方法.如采用粗糙集理论，建立发动机状态参数与单元体维修级别之间的规则库［6］.采用基于元模型的反向传播学习算法，建立具有自适应能力的维修工作范围决策知识库［7］等.基于建立的规则库和知识库，经过推理获得发动机维修工作范围.这类方法存在的主要问题是发动机维修工作范围的合理性取决于建立的规则库，当发动机送修样本较少时，往往难以建立有效的规则库.3)基于模型的方法.这类方法将发动机维修工作范围优化问题抽象为一个函数优化问题，通过对模型的求解获得发动机维修工作范围.如文献［8］将多台送修发动机的单元体维修级别、组件更换策略看成是一个多目标优化问题，采用层次分析法和遗传算法对优化问题进行了求解.该优化模型没有考虑目前航空公司普遍采用的排气温度裕度、燃油流量等送修目标值，从而影响了它的实用性.文献［9］提出了一种面向目标的发动机维修工作范围决策方法，从寿命件、软时限、排气温度裕度(Exhaust Gas Temperature Margin，EGTM)、硬件损伤、适航指令/服务通告5个方面进行单元体维修级别的制定;针对决策过程中单元体性能恢复值分配存在的难点，建立了以维修成本最小为目标的优化模型，分别采用动态规划和启发式算法对模型进行了求解.

文献［9］较好地解决了发动机维修工作范围决策问题，但仅适用于能够准确给出各单元体不同维修级别能够恢复的EGTM的情况.对于新发动机机队，一般难以精确地给出各单元体各维修级别能够恢复的EGTM，即各单元体各维修级别能够恢复的EGTM是不确定的.本文对这种情况下的发动机维修工作范围决策问题进行研究.

1 确定条件下单元体性能恢复值分配优化模型

单元体性能恢复值分配优化是指根据送修发动机的性能目标确定各个单元体的维修级别，使得在满足性能目标的前提下维修成本最小.性能指标一般是EGTM.为了叙述方便，沿用文献［9］的约定及符号.

1)组成发动机的单元体数量为n，第i个单元体表示为Mi;

2)对于单元体Mi，其初始维修级别表示为Wi，0，可选的维修级别的总数，即级别不低于 Wi，0的维修级别的总数记为mi+1，使用Wi，ji表示第ji个可选维修级别，0 ≤ ji≤ mi，Wi，ji和 Wi，0相比，增加的 EGTM 恢复值为 ti，ji，增加的维修成本为 ci，ji，对于 0 ≤ a ≤ b ≤ mi，不妨设 ti，a≤ ti，b，且 ci，a≤ci，b;

3)所有单元体还需恢复的EGTM记为t*;

确定条件下的单元体性能恢复值分配优化模型如式(1)所示，具体求解方法请参考论文［9］，本文不再赘述.

式(1)中，xi表示Mi可以选择的维修级别的编号.

2 单元体性能恢复值的模糊化

当不能准确给出不同单元体不同维修级别能够恢复的EGTM时，与单元体Mi初始维修级别Wi，0相比，维修级别 Wi，ji增加的 EGTM 恢复值就可以表示为一个模糊数.下面给出模糊数的定义.

完成证件打印。从所需动作分析，完成一个证件的打印共需2个水平运动、2个垂直方向运动以及抓纸及松纸动作。水平方向的纵向、横向运动分别由2个气缸控制，抓手的上下移动要求定位准确，采用伺服电机通过丝杆驱动实现垂直方向的进给运动[1]。所有驱动系统的各种动作完成后，均由传感器发出信号来连接相互位置关系。

定义1［10］设是定义在实数域R上的模糊集(x0)表示x0在上的隶属度表示的α－截集.如果满足:1)是正规的，即存在x∈R，使是闭区间.那么称为模糊数.

在误差允许的范围内，一般模糊数都可以采用梯形模糊数逼近［11］;因此，采用梯形模糊数表示维修级别 Wi，ji增加的 EGTM 恢复值为(ji).如果(ji)最可能的取值区间为［ti1(ji)，ti2(ji)］，最大的左偏差为Δ1(ji)，最大的右偏差为Δ2(ji)，其中，0 ≤ Δ1(ji)≤ ti1(ji)，Δ2(ji)≥ 0，那么(ji)如式(2)所示.

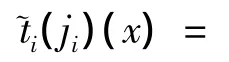
从图1可以看出，当x∈［ti1(ji)，ti2(ji)］时，˜ti(ji)(x)=1;当 x远离区间［ti1(ji)，ti2(ji)］时，˜ti(ji)(x)逐渐变小，直到为0.

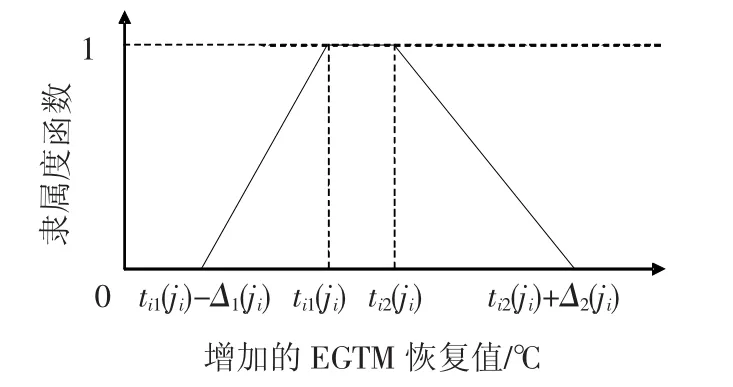
图1 单元体性能恢复值的隶属函数

3 不确定条件下的单元体性能恢复值分配问题建模

对于约束条件含有模糊数的数学规划问题，一般可以通过建立模糊机会约束规划模型来进行求解，即将“确定的约束条件”转化为“约束条件的可信性、可能性或必要性以一定的置信水平α成立”［12］.对于单元体性能恢复值分配问题，其确定条件下的约束条件“发动机的组成单元体还能够恢复的EGTM大于或者等于t*”在不确定条件下就转化为“发动机的组成单元体还能够恢复的EGTM大于或者等于˜t*的可能性至少是某一置信水平α”了.

因此，参考式(1)可以建立不确定条件下的单元体性能恢复值分配优化模型如下:

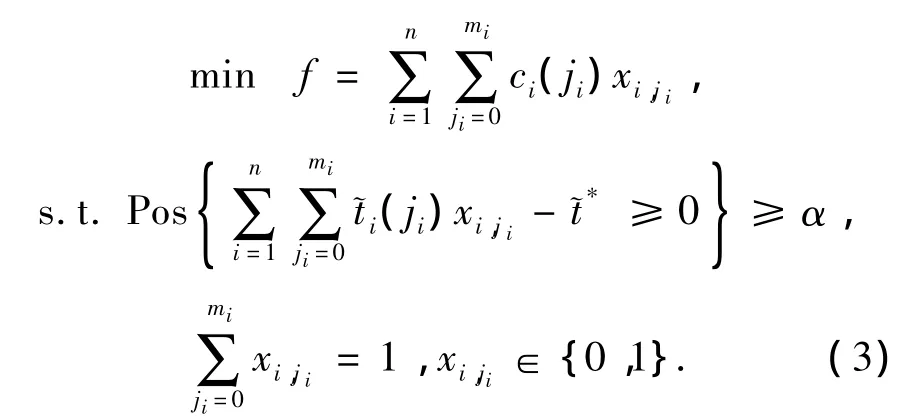
式中，xi，ji是决策变量，表示单元体Mi是否选择维修级别 Wi，ji，如果选择，xi，ji=1，否则 xi，ji=0;是梯形模糊数Pos{·}表示可能性.

模糊机会约束规划模型求解的关键是处理机会约束，常用的求解方法是将机会约束转化为清晰等价类，然后用传统的求解方法对它的等价模型进行求解.

4 基于清晰等价类的求解

为了推导出模型机会约束的清晰等价类，首先给出定理 1［13］.

由式(5)，式(3)表示的模型等价于:

将式(6)中的决策变量xi，ji更换为单元体Mi选择的维修级别编号xi，则式(6)转化为

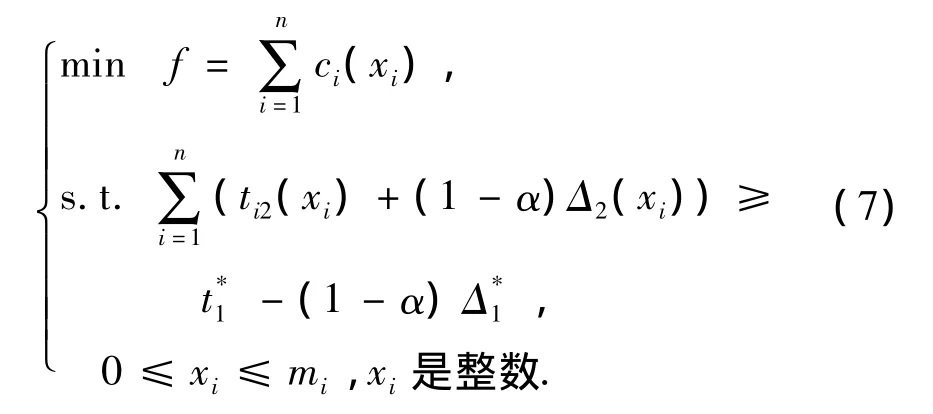
不难发现，式(1)和式(7)表示的模型的结构是完全一样的.因此，对于不确定条件下的单元体性能恢复值分配问题，如果在求解前将和˜t*根据置信水平α替换为，如图2所示，就可以采用文献［9］中的算法进行求解了.

图2 置信水平和单元体性能恢复值的关系

5 应用实例

以一台CFM56－5B发动机为例对本文提出方法的有效性进行验证.样本发动机于2010年2月1日拆下送修.经过综合考虑，确定送修目标为:①修后预计使用的总时间tgoal=15 000 h;②修后预计使用的总循环次数Cgoal=8 000;③修后的排气温度裕度为70℃.表1是中国国际航空公司发动机主管工程师根据发动机历史送修数据给出的经验数据，分别是CFM56-5B发动机各单元体各维修级，如目视检查(Visual Inspection，VI)、最小修理(Minimum，MIN)、性能恢复(Performance，PER)和大修(Full Overhaul，FOH)，对应的最可能的性能恢复值或区间和维修成本.

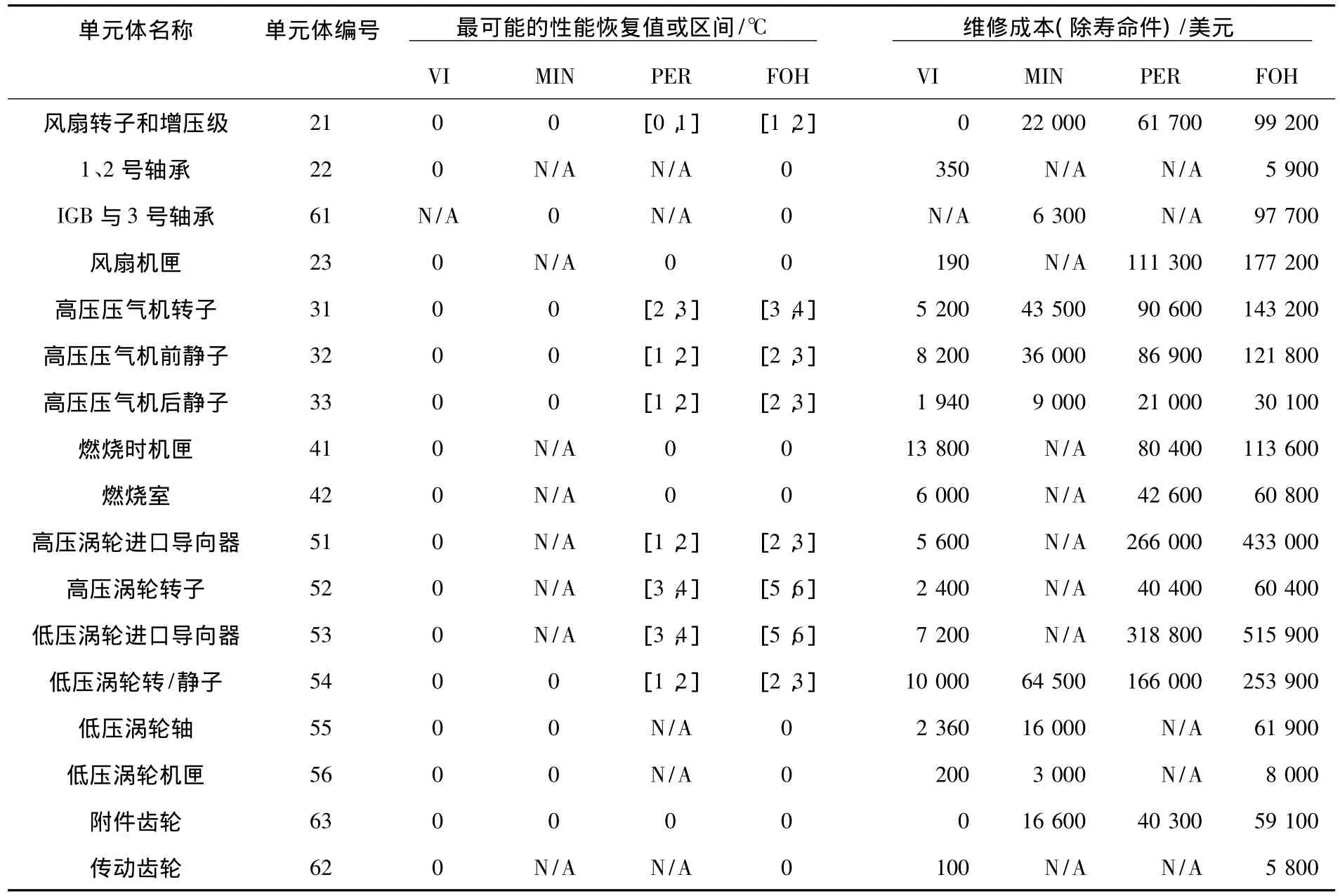
表1 单元体各维修级别对应的最可能的性能恢复值或区间和维修成本

1)根据样本发动机的寿命件小时循环记录，发现高压压气机转子的前轴、后空气封严、高压涡轮转子的后轴、前空气封严等的剩余寿命低于Cgoal，为了满足送修目标②，本次送修必须更换上述零件，以高压压气机转子单元体为例，更换前轴、后空气封严的最低维修级别为FOH，这样就从寿命件角度确定了各单元体的最低维修级别;样本发动机在拆下前的最后一次孔探检查时，发现燃烧室的两个喷嘴间的双孔板上多个位置有烧蚀，并伴有径向裂纹，最长约20 mm，为了满足送修目标①和②，燃烧室单元体的最低维修级别为PER;根据单元体小时循环记录，发现所有单元体均没有达到性能恢复的软时限，只需进行目视检查.综上，从寿命件、软时限、部件损伤、适航指令/服务通告这4个方面确定的单元体初始维修级别如表2所示.

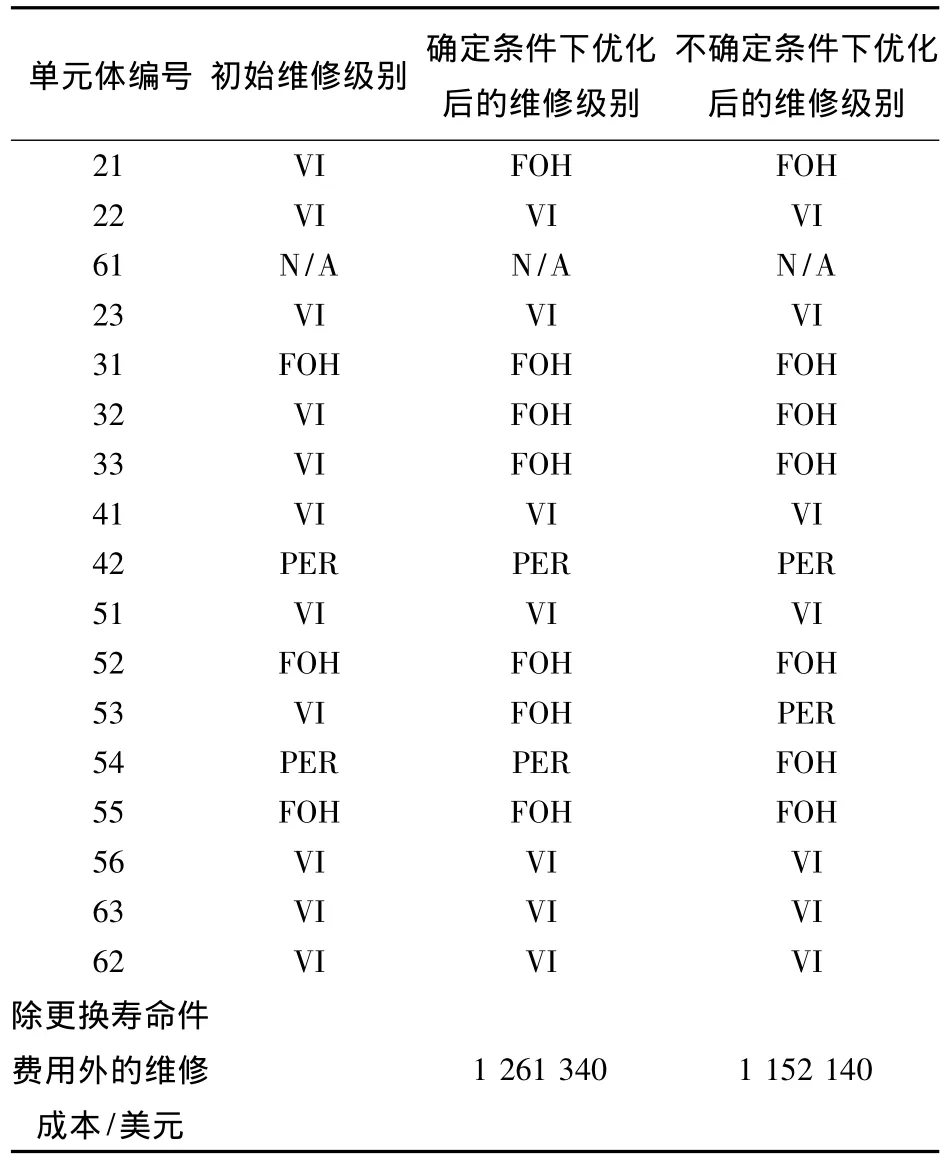
表2 单元体维修级别优化结果

6 结论

1)建立了不确定条件下的单元体性能恢复值分配优化模型，采用基于清晰等价类的求解方法对模型进行了求解，解决了不确定条件下的民航发动机维修工作范围优化问题.

2)与确定条件下的优化模型相比，不确定条件下的发动机单元体性能恢复值分配模型的求解结果与机会约束的置信水平有关.一般来说，置信水平越低，发动机维修成本越低，但实现送修目标的风险也会越高;置信水平越高，实现送修目标的风险越小，但发动机维修成本越高.选择合理的置信水平对获得符合工程实际的决策至关重要.

［1］马乃苍，贾向君，祝华远.航空装备维修思想的发展探讨［J］.航空科学技术，2003(6):27－29.

［2］沈建军.工程机械维修级别决策体系的研究［D］.西安:长安大学，2004:11－40.

［3］JOO S J.Scheduling preventive maintenance for modular designed components:a dynamic approach［J］.European Journal of Operational Research，2009，192(2):512－520.

［4］Air Force SBIR/STTR.Work scope optimization tool contributes to lower maintenance costs and higher reliability in aircraft engines［EB/OL］.2011 －06 －30.http://www.afsbirsttr.com/Publications/Documents/Advantage2＆3Q2009.pdf.

［5］NCMS.Engine work scope optimization for improved reliability and reduced fuelconsumption［EB/OL］.［2011－06－30］.http://ctmaideas.ncms.org/ideas/project－detail.asp?Project－ID=181.

［6］梁剑，左洪福，常继百，等.基于统计粗集模型的航空发动机维修等级预测方法研究［J］.应用科学学报，2005，23(2):196－199.

［7］汤新民.基于Petri网的航空发动机车间维修过程建模及其应用研究［D］.哈尔滨:哈尔滨工业大学，2007:17－34.

［8］WANG J R，YU T B，WANG W S.Integrating analytic hierarchy process and genetic algorithm for aircraft engine maintenance scheduling problem［C］//Proceedings of the 6th CIRP-Sponsored International Conference on Digital Enterprise Technology.Hong Kong:Springer，2009:897－915.

［9］付旭云，钟诗胜，丁刚.民用航空发动机单元体送修工作范围决策［J］.航空动力学报，2010，25(10):2195－2200.

［10］胡宝清.模糊理论基础［M］.武汉:武汉大学出版社，2004:76－88.

［11］PGRZEGORZEWSKI P，MRÓWKA E.Trapezoidal approximations of fuzzy numbers［J］.Fuzzy Sets and Systems，2005，153:115 －135.

［12］刘宝碇，赵瑞清，王纲.随机规划与模糊规划［M］.北京:清华大学出版社，1998:164－183.

［13］KASPERSKI A，KULEJ M.The 0－1 knapsack problem with fuzzy data［J］.Fuzzy Optimization and Decision Making，2007，6(2):163－172.

Civil aeroengine workscope decision-making under uncertain conditions

FU Xu-yun，CUI Zhi-quan，ZHONG Shi-sheng
(Dept.of Mechanical Engineering，Harbin Institute of Technology at Weihai，264209 Weihai，Shandong，China)

To reduce maintenance cost and improve performance after a shop visit，a decision-making method for civil aeroengine workscope under uncertain condition is proposed.Firstly，aeroengine overall performance restoration value for each module's maintenance level is expressed as a trapezoidal fuzzy number，and then a fuzzy chance constrained programming model on module performance restoration value distribution optimization is put forward under uncertain condition.Secondly，the chance constraint of the model is transformed into a clear equivalence class.It is found that this model and the optimization model of module performance restoration value distribution under certain condition have the same structure.Thus，the solving method of the model with certain condition is adopted to achieve the model with uncertainty condition.Finally，the proposed method is validated by a real example.The result shows that the proposed method can solve decision-making problem for aeroengine maintenance workscope under uncertainty condition;the reasonable confidence level for the chance constraint of the model is essential to the decision-making result，and could be determined according to the risk of achieving the repair objectives and maintenance cost.

aeroengine;module;workscope;exhaust gas temperature margin;performance restoration value

V263.6

A

0367－6234(2012)07－0078－05

2011－07－13.

国家自然科学基金委员会与中国民航局联合资助项目(60939003);民航局科技计划项目(MHRD201122);哈尔滨工业大学(威海)校科学研究基金资助项目(HIT(WH)X201107).

付旭云(1981—)，男，博士，讲师;

钟诗胜(1964—)，男，教授，博士生导师.

付旭云，fuxy－hit@163.com.

(编辑 杨 波)