螺旋锥齿轮虚拟加工过程算法

王太勇，邢 元，李 琳，王品才

螺旋锥齿轮虚拟加工过程算法

王太勇1，邢 元1，李 琳1，王品才2

(1. 天津大学机械工程学院，天津 300072；2. 天津大学建筑设计研究院，天津 300072)

为了解决目前螺旋锥齿轮切削仿真中存在的仿真速度慢、精度低、过程不稳定和缺乏独立性等问题，以螺旋锥齿轮齿面成形过程为研究对象，运用“层片切割算法”进行三维实体几何模型动态仿真以及三维切削实时仿真．该算法主要包括建立切削坐标系、刀具数学模型、刀具坐标系的转换模型、层片分割模型、求交计算模型以及相邻切削位置特征点的取舍模型．以此为基础开发的螺旋锥齿轮虚拟加工软件采用Windows作为开发平台，以Visual C++6.0(VC)作为基础编程语言，利用OpenGL图形库进行图形显示并将齿轮模型数据以规定格式输出．经验证，该算法求交速度快、结果精确，相关开发软件可靠准确．

螺旋锥齿轮；层片分割算法；虚拟加工

螺旋锥齿轮属于复杂曲面零件的一种，设计和加工过程复杂，往往需要通过对切齿过程进行仿真来初步验证所使用加工调整参数的合理性．同时，由切削仿真得到的精确几何模型还可用于齿面接触分析和有限元分析，进而在虚拟环境中确定所加工出的齿面是否满足使用要求．目前，很多螺旋锥齿轮加工仿真系统均建立在已有三维造型仿真软件基础上[1-3]，增加了使用成本，降低了开放程度，且利用已有仿真软件及仿真方法“加工”出的螺旋锥齿轮模型精度仍然较低，与实际加工得到的齿轮模型不一致，无法为后续的齿面接触分析(TCA)等提供足够精确的模型．已有的一些多轴数控仿真算法[4-11]也不适用于螺旋锥齿轮齿面成型仿真过程．虽然国外一些公司所开发的螺旋锥齿轮制造专家系统(GEMS系统)已经取得很大成果，建立了基于计算机网络的一体化制造系统，但由于涉及到技术保密问题，公开发表的数控螺旋锥齿轮仿真系统资料很少．

为此，笔者针对目前螺旋锥齿轮切削仿真中存在的仿真速度慢、精度低、过程不稳定和缺乏独立性等问题，提出了基于“层片切割”的齿面成型过程仿真算法以实现螺旋锥齿轮虚拟加工过程，建立具有独立环境和能够真实模拟整个加工过程并得到精确齿面数据信息的仿真系统．

1 螺旋锥齿轮的层片分割算法

本文结合螺旋锥齿轮形状特征和切削过程特点，采用“层片分割”算法进行刀具和轮坯的布尔运算．首先根据螺旋锥齿轮的几何形状，将其分割成有限相似的几何特征，即分割特征集，再建立分割特征的数学模型，后续通过求解数学模型的方法得到齿面数据点信息，以实现虚拟加工．

利用层片分割法进行层面离散时需要考虑2个因素．一是毛坯形状特征．它决定了层片分割方式．选择一个好的分割方式可以简化特征点的取舍过程，使特征点的取舍更加容易．二是毛坯加工区域．在进行求交计算前，先确定毛坯加工区域，再由加工区域确定层片分割范围，可在很大程度上削减冗余计算，减小计算量，从而缩短计算时间．

以成形法铣削加工大轮和刀倾法铣削加工小轮为例，铣齿加工均采用具有直线刃铣刀盘来进行，简化后的铣齿刀具的内刀和外刀可被看作内锥面和外锥面(见图1)．加工时，刀具直线部分加工出齿轮啮合面部分，顶端切削刃加工出齿轮的根锥面．在大轮和小轮加工过程中，沿齿轮锥面法向方向上的加工区域均为面锥和根锥之间的区域，因此可以在此区域内对毛坯进行层片分割．如图2所示，大轮加工区域为A点所在圆和B点所在圆之间的圆台面，小轮加工区域为C点所在圆和D点所在圆之间的圆台面．锥面层片分割结果如图3所示．

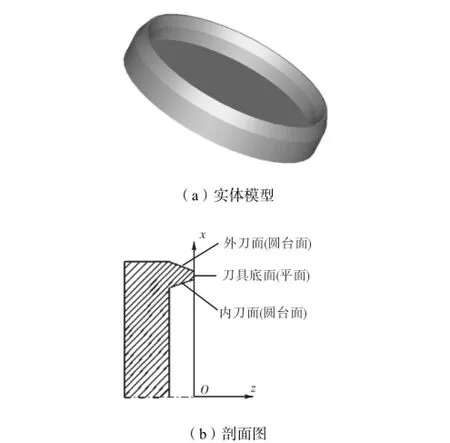
图1 简化后的刀具模型Fig.1 Simplified cutting tool model

图2 加工区域Fig.2 Cutting area

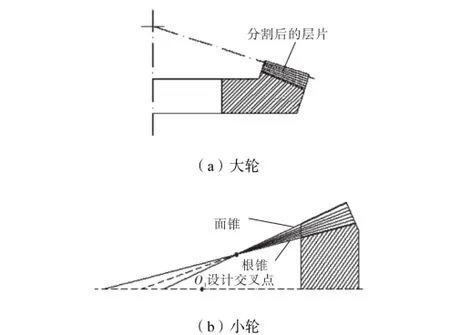
图3 锥面层片分割结果Fig.3 Cone slicing results

为求得刀具直线刃部分加工出的啮合面部分，首先将螺旋锥齿轮齿坯在面锥和根锥之间分解为一系列的圆台面，然后在每个锥面上引出等角度间距的射线(见图4)，射线方程为式(1)．将刀具与射线进行求交运算，所得交点即为啮合齿面上的点(见图5)，也就是说所有分割特征与刀具交点组成的点集构成整个啮合齿面．

式中：3α为射线所在锥面的压力角；cR为射线所在圆锥面的上底面半径；3u为射线上某一点距该射线上1z坐标为-L的点的距离；3θ为射线与1x轴的夹角.

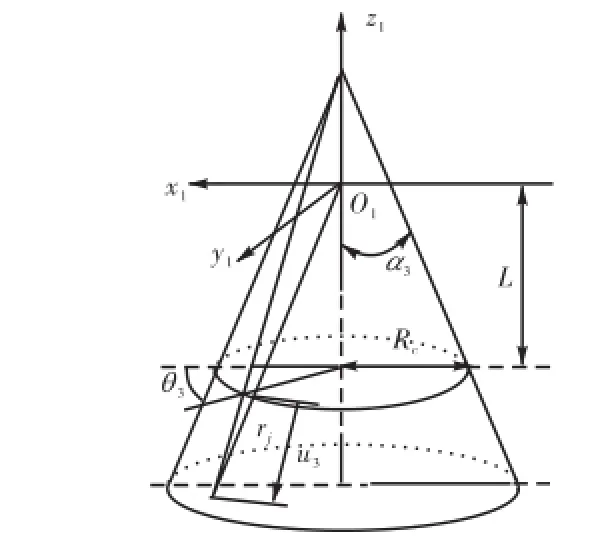
图4 锥面上射线Fig.4 Ray construction from cone

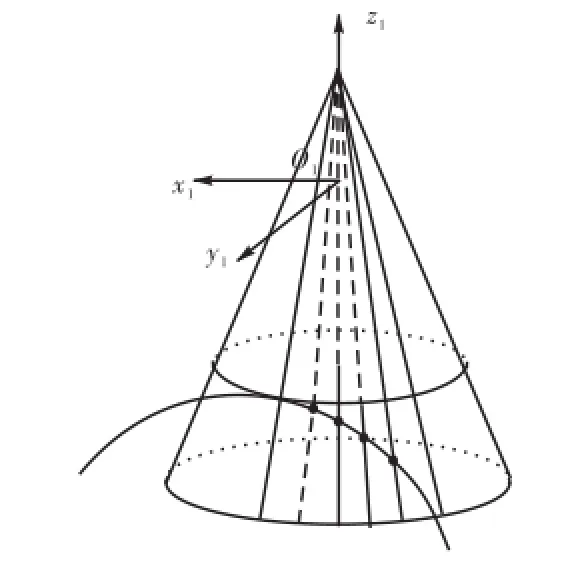
图5 刀具与射线交点Fig.5 Intersection point of cutting tool and the ray from cone

为求得刀具底刃加工出的齿底部分，可在根锥面上引出垂直于锥面的一系列射线(见图6)，刀具底刃与射线交点集组成齿底．其射线方程为

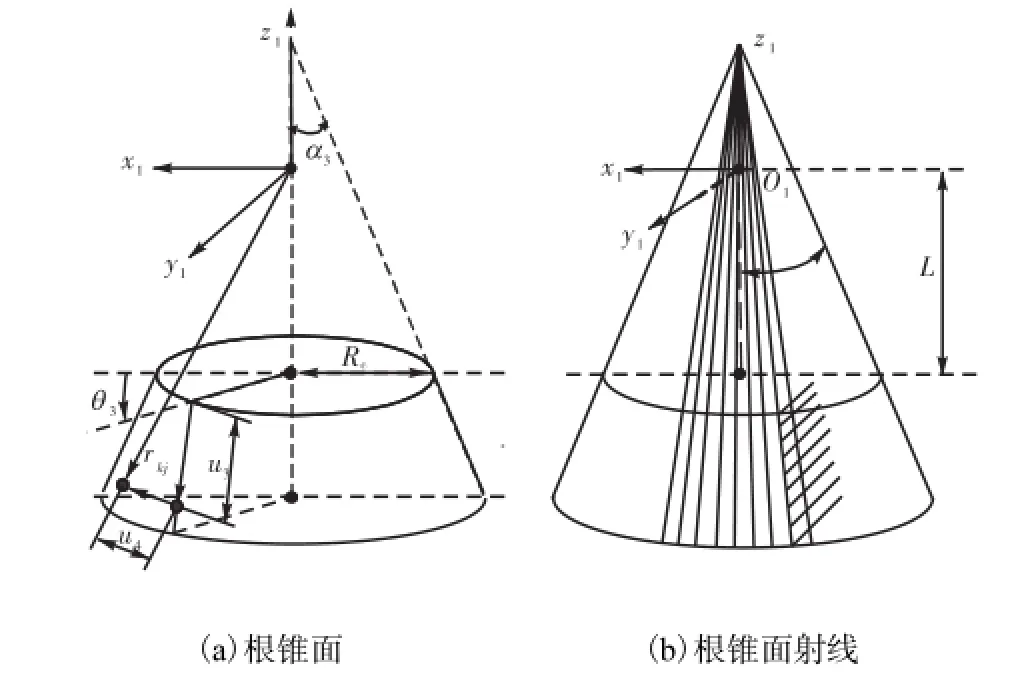
图6 与根锥面垂直的直线生成Fig.6 Vertical ray construction from root cone

式中：3α为射线所在锥面的压力角；cR为根锥面的上底面半径；4u为射线的长度．

2 切削过程求交计算

在实际加工过程中，切削是逐步进行的，这一过程在仿真中是通过计算一系列离散时间的有效特征集来实现的．切削过程求交，即求取每一时刻刀具与毛坯相交的特征．所求得刀具与齿坯层片分割后的分割特征集在每一时刻的交点，它们的集合便是实际加工过程中刀具与毛坯相交特征的离散值．在求交过程中，还存在着相邻2个时刻的特征集中元素的取舍问题．在对特征集中的元素进行取舍时应坚持一个原则：在切削的过程中，毛坯的坯料是逐渐减少的．计算时可为特征集中的元素设置标志量，根据标志量对相邻2个时刻的特征集中的元素进行取舍．

以成形法加工大轮为例，点的取舍可以选择3θ和3u作为标志量，如图7所示，在同一射线上，相邻2个刀位切削所得特征点的取舍可根据3θ和3u进行判断．由于切削过程中轮坯的材料不断减少，所以对于外刀面切削，当2点3θ值相同时应保留3u值较大的点；而内刀面切削刚好相反，应该保留3u值较小的点．对于只有在当前刀位才与切削刀面有交点的射线来说，直接将特征点保留即可．整个取舍过程实际上取决于成形法加工点的特点，即当前刀位切削所得特征点完全取代上一刀位切削所得特征点，因此大轮切削过程中点的取舍较容易．

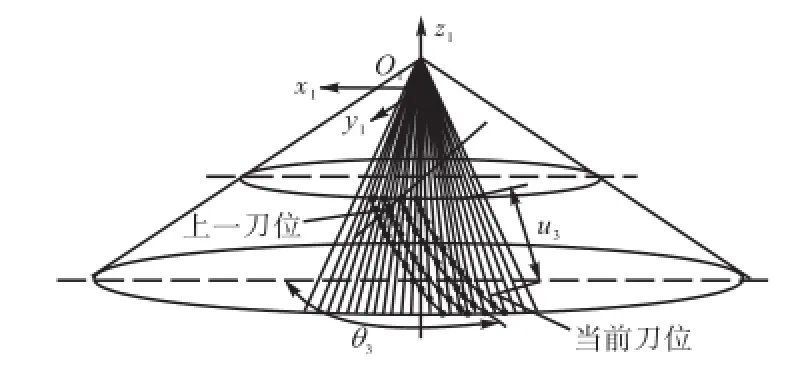
图7 成形法加工大轮时点取舍判断方法示意Fig.7 Sketch of point selection approach in wheel format machining

与成形法加工大轮相比，刀倾法加工小轮的加工过程较复杂，因此点的取舍要复杂得多．以齿坯层片分割后的一个圆台面与外刀面相交的特征点取舍为例，将3θ和3u作为取舍标志量，根据其取舍情形可分为以下3种情况．

(1) 完全替换．如图8(a)所示，此种情况与成形法加工大轮中前后两刀位关系类似，可用当前刀位切削所得的特征完全取代上一刀位的特征，即用在当前切削位置上刀具切削面与分割特征的交点集代替上一切削位置上刀具切削面与分割特征的交点集，并将其作为描述当前切削位置上本分割锥面上的特征点集．具体的取舍方法为前后2个切削位置的点集中的点所在射线θ3值相同时，保留u3值较大的点．

(2) 部分替换．如图8(b)所示，此时刀具和齿坯在相邻2个切削位置上有部分区域重合．且前后2次的重合区域不是包含与被包含的关系，而是有部分相交，也就是说，后一切削位置上刀具切削面与分割特征的交点集应部分取代前一位置上刀具切削面与分割特征的交点集．即当前切削位置上齿面特征点集的取舍为：Q点所在射线左侧射线上取上一切削位置计算所得特征点集，即u3值较大的点；Q点所在射线右侧射线上取当前切削位置计算所得特征点集，即u3值较大的点．

图8 刀倾法加工小轮时点取舍判断方法示意Fig.8 Sketch of point selection approach in pinion generation machining

(3)不替换．如图8(c)所示，在此切削位置，刀具外刀面与齿坯没有交点，即当前切削位置上齿面特征点集应为上一切削位置计算所得特征集．取舍原则为，前后2个切削位置的点集中的点所在射线3θ值相同时，应保留3u值较大的点．

3 算 例

本文开发的螺旋锥齿轮加工仿真系统建立在Windows开发平台下，使用Visual C++6.0编程工具实现．其可视化过程主要通过OpenGL标准图形库进行显示．为了满足不同切削加工仿真的需求、增强仿真环境的可重复利用性，同时又可以为仿真提供基本数据，建立了参数化刀具和毛坯生成模块，通过建立刀具和毛坯简化数学模型和数据接口，将模型参数化，并通过输入参数控制刀具和毛坯的几何尺寸．

在对切削过程实现可视化仿真的过程中，需要建立与实际加工相同的运动模式．仿真中运动的实现实际上是通过不断改变每一刷新时刻各部分模型的显示位置实现的，其运动是各自独立的．但是必须保持显示过程中机床的运动、刀具的运动和齿坯的运动变化一致．这一过程可通过利用控制参数建立不同的绘图坐标系实现，其中，控制参数即机床的运动参数．本仿真系统中所显示的机床模型是利用已有的三维造型软件建立的STL模型，通过在VC工程中读取相应部件的STL模型并渲染，可以将其显示在仿真环境中．在建立各个部件的STL模型时，可以使各个部件均处于机床坐标系下．在机床的运动过程中，不断地改变机床各部件在机床坐标系下的位置即可实现对机床的仿真．

为了验证软件的可靠性和准确性，基于天津天大精益数控技术有限公司的TDNC-W200加工中心，利用表1所示的齿坯、刀具和加工调整参数，进行螺旋锥齿轮大轮成型法虚拟加工仿真及设计加工．加工机床和加工结果如图9所示，虚拟加工结果与实际加工结果显示了很好的一致性．

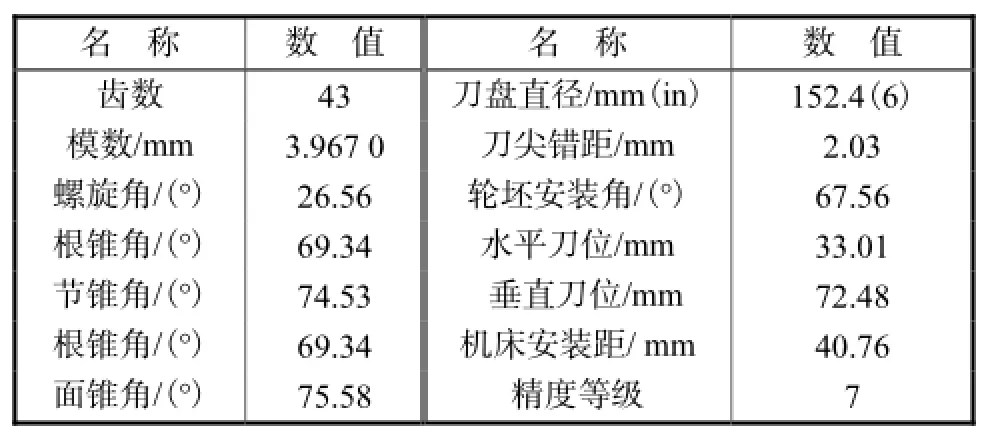
表1 大轮设计参数与加工基本参数Tab.1 Wheel design parameters and machining parameters

图9 大轮成形法加工仿真与实切Fig.9 Wheel visual format machining and real format machining

为了避免机床精度对仿真结果的影响，将自行开发的仿真系统仿真结果与在Solidworks中通过宏程序建立相同参数的切削模型进行仿真的结果进行对比．具体做法为，在齿轮凹面上取5×6点阵，即在5个分割层片上分别按一定间隔取凹面上的6个点，做数据对比．如图10所示，测量结果表明自开发仿真系统与Solidworks 仿真系统的仿真结果对比差值数量级为10-4m，即本算法所得点的精度达到10-4,m数量级．因此，本算法计算结果准确、方法可行．

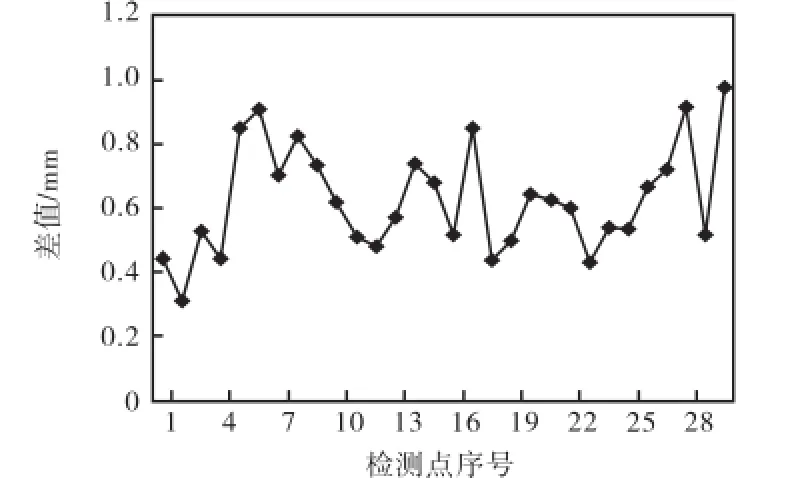
图10 自开发仿真系统与Solidworks仿真系统的仿真结果差值Fig.10 Difference between the results from self-developed system and those from Solidworks

4 结 语

本文根据螺旋锥齿轮齿面成形过程的特点，针对目前仿真中存在的速度慢、精度低的问题，提出了“层片分割”算法，即先将齿坯模型进行层片分割并建立分割特征的数学模型，然后将刀具数学模型转换到齿轮坐标系下，求解刀具切削面与分割特征的交点并对其进行取舍，最后得到每一切削时刻的齿面数据点．通过建立切削坐标系、刀具数学模型、刀具坐标系的转换模型、层片分割模型、求交计算模型以及相邻切削位置特征点的取舍模型，在虚拟仿真环境中利用程序实现了这一算法的建立过程．校验结果表明，该算法求交精度较高，方法可行，相关开发软件可靠准确．在后续的TCA分析中，可以通过仿真系统得到的比较精确的齿面数据点进行曲面重构，从而进一步提高齿面接触分析的精度．此算法虽然在文中主要针对螺旋锥齿轮进行仿真，但是由于其快速性和精确性，也可以通过进一步研究将其应用于五轴甚至多轴的数控加工中心仿真系统．

［1］ 熊越东，王太勇，张 威. 螺旋锥齿轮数控铣齿加工过程几何仿真研究[J]. 机床与液压，2005(6)：1-3，88.

Xiong Yuedong，Wang Taiyong，Zhang Wei. Research on NC gearing geometric simulation of spiral bevel and hypoid gears[J]. Machine Tool and Hydraulics，2005 (6)：1-3，88(in Chinese).

［2］ 唐进元，蒲太平，颜海燕. 螺旋锥齿轮双重双面法多轴联动数控加工计算机仿真研究[J]. 制造技术与机床，2008(2)：25-29.

Tang Jinyuan，Pu Taiping，Yan Haiyan. Research on simulation system of duplex spread blade multi-axis machining for spiral bevel gears[J]. Manufacturing Technology and Machine Tool，2008(2)：25-29(in Chinese).

［3］ 纪玉坤，曹利新. 基于UG的五轴数控机床加工仿真[J]. 计算机仿真，2006，23(1)：215-218.

Ji Yukun，Cao Lixin. 5-axis machining simulation based on redevelopment of UG[J]. Computer Simulation，2006，23(1)：215-218(in Chinese).

［4］ Chappel I T. The use of vectors to simulate materials removed by numerically controlled milling[J]. Computer Aided Design，1983，15(3)：156-158.

［5］ Jerard R B，Drysdale R L，Hauck K. Methods for detecting errors in numerically controlled machining of sculptured surfaces[J]. IEEE Computer Graphics and Applications，1989，9(1)：26-39.

［6］ Blackmore D，Leu M C，Wang K K. Application of flows and envelopes to NC machining[J]. CIRP Annals，1992，41(l)：493-496.

［7］ Blackmore D，Leu M C，Wang L P. Sweep-envelope differential equation algorithm and its application to NC machining verification[J]. Computer Aided Design，1997，29(9)：629-637.

［8］ 王占礼，胡艳娟. 三轴数控铣削加工中心仿真系统[J]. 机械工程与自动化，2006(2)：90-92，95. Wang Zhanli，Hu Yanjuan. Simulation system of threeaxis NC milling machining center[J]. Mechanical Engineering and Automation，2006(2)：90-92，95(in Chinese).

［9］ 黄正东，曾祥林，王启付，等. 基于全Z-Buffer的五轴铣削图形仿真[J]. 华中理工大学学报，1996，24(1)：60-63.

Huang Zhengdong，Zeng Xianglin，Wang Qifu，et al. Graphical simulation for 5-axis milling based on full ZBuffer[J]. Journal of Huazhong University of Science and Technology，1996，24(1)：60-63(in Chinese).

［10］ 陈良骥，刘元朋，王永章. 五轴数控加工材料去除过程仿真方法的研究[J]. 机械制造，2007，45(9)：9-11.

Chen Liangji，Liu Yuanpeng，Wang Yongzhang. Study on the approach to simulating material cutting process on 5-axis NC machine[J]. Machinery，2007，45(9)：9-11(in Chinese).

［11］ 郭晓冬，张明德，梁 伟. 基于AutoCAD的锥齿轮切齿过程仿真及软件开发[J]. 现代制造工程，2002(10)：34-36.

Guo Xiaodong，Zhang Mingde，Liang Wei. Simulation of spiral bevel gear machining and development of the related software on the basis of AutoCAD[J]. Modern Manufacturing Engineering，2002(10)：34-36(in Chinese).

Visual Machining Algorithm of Spiral Bevel Gear Forming Process

WANG Tai-yong1，XING Yuan1，LI Lin1，WANG Pin-cai2
(1. School of Mechanical Engineering，Tianjin University，Tianjin 300072，China；2. Tianjin University Research Institute of Architecture Design and Urban Planning，Tianjin 300072，China)

Since many problems exist in the simulation of spiral bevel gear machining，like slow speed，low precision，unstable process，lack of independence and so on，a visual simulation system of 3D real machining was constructed by slice algorithm on the basis of spiral bevel gear forming process in this paper. The algorithm includes cutting coordinate system construction，cutting tool modeling，cutting tool coordinate system transforming，slice modeling，calculation modeling and point selection at adjacent position. Then the spiral bevel gear machining simulation software was developed on Windows by Visual C++6.0 and OpenGL graphics library，which will output gear model and data document. Experiment proved that this visual simulation algorithm has advantages in fast speed and high precision，and that the related software is reliable and correct.

spiral bevel gear；slice algorithm；visual machining

TH132.41；TP391.9

A

0493-2137(2012)02-0116-06

2010-09-30；

2011-04-28.

国家自然科学基金资助项目(50975193)；国家高技术研究发展计划(863计划)资助项目(2007AA042005).

王太勇（1962— ），男，教授，博士生导师，tywang@139.com.

邢 元，smileinsun1123@yahoo.com.cn.