高精度动平衡测量中不平衡信号提取方法研究

李传江，费敏锐，张自强

(1.上海师范大学 信息与机电工程学院，上海 201418，2.上海大学 机电工程与自动化学院，上海 200072)

动平衡测量系统广泛用于旋转机械的生产和维护中，提高测量系统精度可以节省转子的平衡时间和降低转子平衡的成本。动平衡测量的原理是:电机驱动转子旋转，通过对安装在机架支承处的振动传感器信号的调理、滤波和分析得到不平衡量的大小和相位。由于动平衡测量牵涉到驱动激励、信号转换、调理、传输以及分析处理等多个环节，有用信号除受电气干扰外，还受检测设备本身其他运动部件的振动串扰，检测到的振动信号往往受到严重污染，尤其是在低转速、变频驱动等场合，信噪比恶化严重。因此，提高动测量精度的核心是从含有噪声的信号中准确提取出不平衡信号。

为方便不平衡信号的准确提取，通常需要信号滤波技术来滤除噪声信号，提高信噪比，同时采用增益调整环节改变信号幅值以便减少AD采样的误差。近年来，基于开关电容的自动跟踪滤波技术在动平衡领域得到了广泛的应用［1］，为降低硬件成本，增加可靠性，刘健等［2］提出了软件实现的数字跟踪滤波器，杨克己等［3］提出一种自适应滤波技术，成功应用到动平衡测量系统中。不平衡信号的提取方法是影响动平衡测量精度的关键因素，常用的方法有快速傅里叶变换法(FFT)、正交相关法［4］、正弦参数搜索法［5］等，前两种方法的精度相当，且都需要对振动信号进行整周期采样，但二者的计算量不同。正弦搜索法虽不需要整周期采样，但是运算时间较长，用于测量速度要求不太高的场合。通过软件的方式实现准整周期测量具有成本低、可靠性高的优点，被广泛应用于信号提取中。

通过大量的现场试验发现，当不平衡较小时，现有的动平衡测量系统大多会出现测量结果不稳定、重复性差等问题，普遍采用多次测量求平均值的方法来减小测量结果的波动。但当出现机械或电测系统的近频干扰导致振动信号出现拍频现象时，求平均值的方法收效不大，尤其是不平衡量相位值很难准确测量。本文提出一种估算拍频周期的方法和采用正弦逼近法提取不平衡量幅值和相位的方法，仿真和实验结果表明，该方法可以提高不平衡信号的提取精度。

1 信号处理系统构成

如图1所示，动平衡测量中振动信号处理系统由模拟处理和数字处理两部分组成，模拟处理部分包括前置处理电路、自动增益控制电路，模拟处理后的信号经过AD转换模块进入微处理器，并由软件实现数字信号处理算法，该算法包括带通跟踪滤波、整周期数据抽取以及幅值和相位提取模块。振动传感器一般选用性价比较高、安装较方便的压电传感器，前置处理部分主要完成电荷放大、积分处理和低通滤波的功能，其中积分环节起到消除转速对不平衡信号的影响，同时具有对高频信号的抑制作用。自动增益控制有利于拓宽测量范围和提高测量精度［6］，通常采用微处理器输出开关信号控制电子开关切换电阻网络来实现不同放大倍数间的切换，通过一定的增益控制算法来实现档位的自动切换。

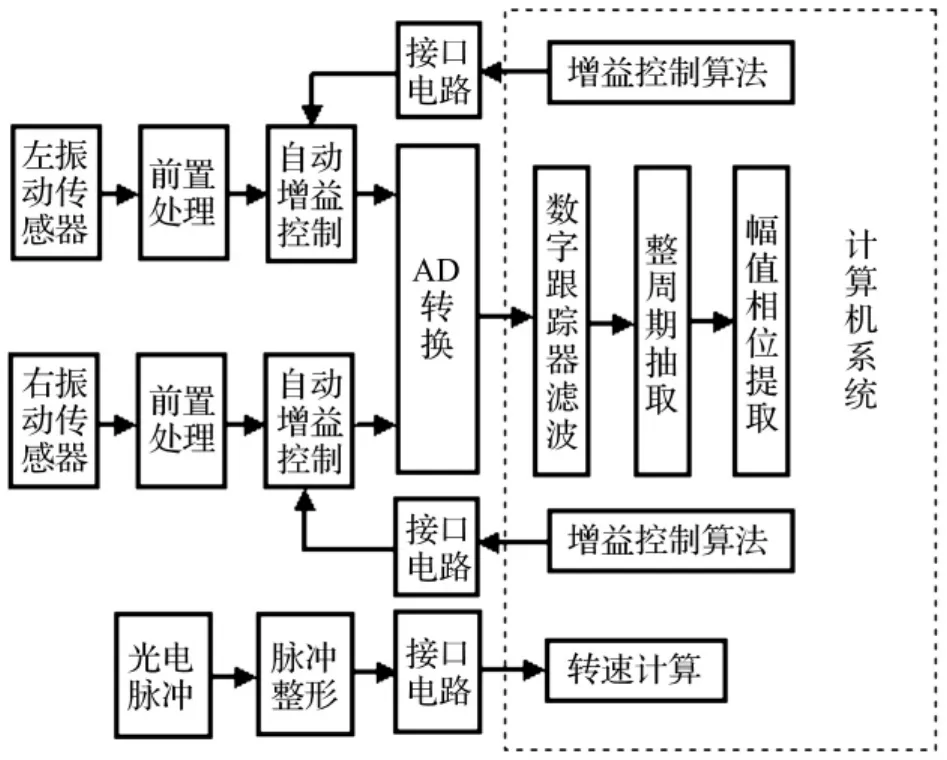
图1 信号处理系统组成Fig.1 Composition of signal processing system

虽然基于开关电容的带通跟踪滤波技术在动平衡测量中广泛被采用，但对于高精度动平衡测量系统该方法有两个缺点:①需要时钟信号，一般为中心频率的50或100倍，不仅增加硬件成本，脉冲信号还会对模拟振动信号带来干扰，且可靠性也会降低;②当信噪比较差时，滤波器输入和输出端的信号峰值相差较大，用滤波输出信号经AD采样后用来控制前端的增益控制模块会导致增益控制效果不佳，甚至会出现信号失真的情况。因此，这里采用软件的方法实现数字带通跟踪滤波［2］，不仅节省了硬件成本，提高了可靠性，也便于提高自动增益控制模块的性能。

2 不平衡信号提取方法

2.1 不平衡信号提取方案

经过带通跟踪滤波后的信号中主要成分是不平衡量引起的振动信号，同时还可能含有由于机械或电测系统引起的与不平衡振动信号频率相近的信号成分，二者合成在一起会出现拍频现象，即振幅随时间作周期性变化，其周期大小由两个信号的频率之差确定。传统的不平衡信号提取方法是根据一个旋转周期内的振动数据得到不平衡信号的幅值和相位，当不平衡量较小或信噪比较差时传统测量系统大多采用多次测量求平均值的方法来提高测量稳定性，但当产生拍频现象时，连续多个周期内的振动信号幅值和相位相差较大，每次测量的结果都不准确，即便多次测量结果取平均值也无法得到准确的测量结果，尤其是不平衡量的相位既不准确，也不稳定。考虑到通用动平衡测量系统既要求常规测量时的快速性，又要求精准测量时的准确性，本文采用如图2所示的处理流程解决上述问题。

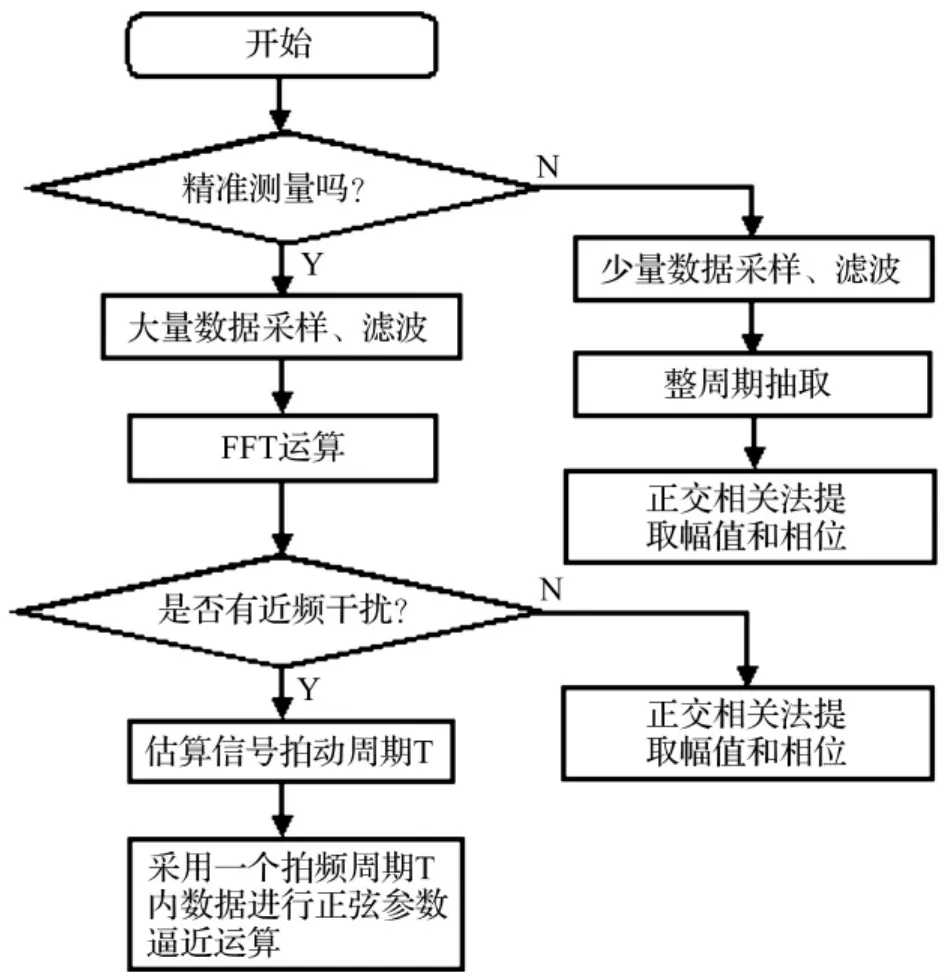
图2 不平衡信号提取流程Fig.2 Unbalance signal extraction process

精准测量功能有两种开启模式:由用户选择设定，或系统根据信号幅值变化情况自动切换。当精准测量未开启时，只需采集少量振动数据，经数字带通滤波后截取一个整周期数据(根据两个相邻的键相脉冲上升沿来截取)，采用正交相关法提取不平衡信号的幅值和相位，在保证一定精度的前提下，尽量提高测量的快速性。当精准测量功能开启时，需要采集多周期内的大量数据，以便提高FFT运算的频率分辨率。在FFT运算的结果中搜索不平衡信号频率附近的信号成分，从而判断是否存在近频干扰，若不存在则采用全部数据进行正弦参数逼近运算，得到不平衡信号的幅值和相位;若存在近频干扰，则先估算拍频信号的周期，然后利用一个拍频周期内的数据进行正弦参数逼近运算，得到不平衡信号的幅值和相位。上述处理流程中的关键技术有两点:① 拍频周期的估算;② 幅值和相位的提取方法。

2.2 拍频周期估算

因为经过带通跟踪滤波后的信号中只含有旋转频率f0附近的信号成分，所以在FFT运算的结果中只搜索f0左右5 Hz内有无明显干扰信号(根据信号幅值与不平衡信号幅值做比较确定)，并提取干扰信号频率记作f1，则拍频周期近似为:，此估算的误差来源于f1的误差，因为f1受到FFT运算点数的影响，其频率分辨率影响f1的精度，这里采用增加运算点数来提高频率测量的精度。若信号中含有多个近频干扰(此现象不常见)，则按照与转子旋转频率最接近的干扰信号的频率来估算拍频周期。

2.3 不平衡信号的提取方法

常用的不平衡信号提取方法有FFT、正交相关法和正弦逼近法。FFT算法和正交相关法虽然推导过程不同，但结论是一致的，由于FFT在蝶形运算过程中不可避免的计算出动平衡测量中无用的高次谐波分量，因此在采样点数N大于16时，它的计算量远大于正交相关法［4］。同时二者都需要整周期采样数据，以避免相位泄露。对比上述两种方法，当信噪比较好时采用正交相关法提取不平衡信号的幅值和相位。

当不平衡量很小，且不平衡信号的波形出现拍频现象时，拍频周期与不平衡信号的周期不一定存在倍数关系，此时无法在一个拍频周期内得到整周期数据，如果采用FFT或正交相关法将会出现相位泄露情况，因此，此时采用正弦逼近法提取不平衡信号的幅值和相位，该方法的原理如下:

正弦信号表示为:

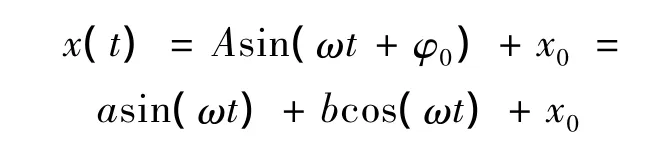
其中:ω=2πf，f是已知的不平衡信号的频率。对含有噪声的振动信号进行采样并滤波处理后得到数据序列xi(i=0，1，2…N －1，N 为采样序列的点数)，由 xi通过最小二乘法拟合可估计出参数a，b，x0。则不平衡信号的幅值和相位为:

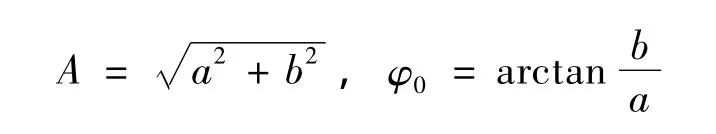
上述数据序列xi为一个拍频周期内的数据，且数据序列的起始处由键相信号的上升沿决定，以此来确定不平衡信号的相位。

3 仿真研究

为验证存在拍频现象时该不平衡信号提取算法的性能，构造如下信号:

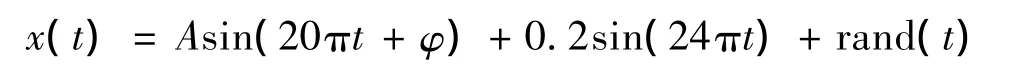
不平衡信号的频率为10 Hz，幅值为A;近频干扰信号的频率12 Hz，幅值为0.2;随机干扰信号的最大幅值为0.1。当不平衡信号取不同的幅值时，采用上述动态识别拍动周期的方法，使用多个周期的数据进行正交相关运算得到的结果如表1所示。

从表中的数据可以看出，当有用信号幅值大于近频干扰信号幅值时，尽管还存在随机干扰信号，幅值和相位提取的精度都很高;当由于信号幅值小于近频干扰信号的幅值时，该方法仍能较为准确的提取出幅值和相位信号，该精度完全可以满足小不平衡量情况下动平衡测量的要求。

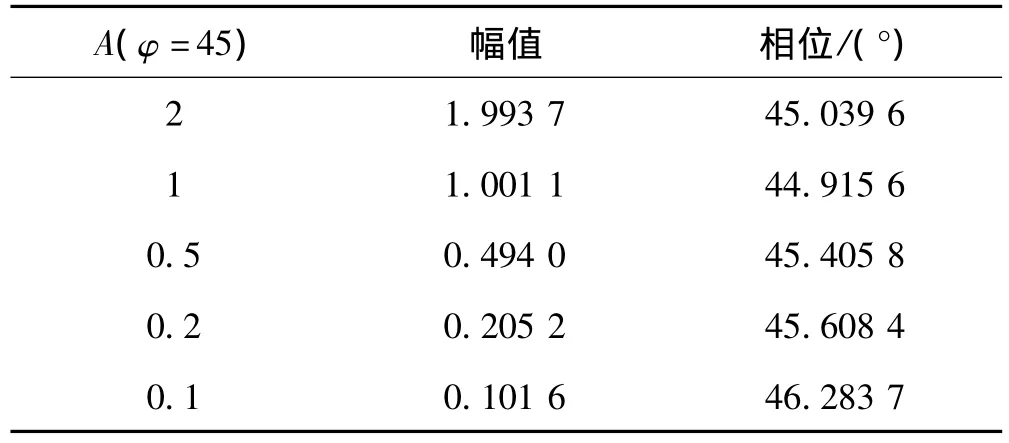
表1 不平衡信号提取结果Tab.1 Result of unbalance signal extraction

4 实验研究

根据本文的信号处理方法设计了基于PC机的动平衡测量系统，采用上述不平衡信号提取方法，与原测量系统进行对比(原测量系统采用硬件带通滤波，采用软件预估整周期采样和FFT不平衡信号提取方法)。

实验采用160kg标准转子，平衡转速为 600 r/min，左右校正面加重半径均为265 mm。测得左侧振动信号的波形如图3所示，带通滤波的Q值取15，经过数字带通滤波后的波形如图4所示，带通滤波不仅消除了直流分量，还对高低频干扰以及随机干扰起到了很好的抑制作用，波形的前10个周期为动态过程，计算不平衡信号使用第10个周期后的数据。将带通滤波后的数据作FFT运算，不平衡信号频率附近的频谱如图5所示，除了在10 Hz附近幅值为0.09的不平衡信号外，还有9.5 Hz附近幅值为0.02的干扰信号，此时拍动的周期约为2 s。

由于传统国标中的最小可达剩余不平衡度(emar)没有考虑相位因素，本文采用文献［7］中的 emar测试方法，同时考虑幅值和相位的准确度，应用本文的不平衡信号提取方法与原测量系统分别做实验，采用相隔45°的8个不同相位点上的数据来计算emar，前者的值为0.28 g·mm/kg，后者的值为 0.5 g·mm/kg。结果表明本文的精准测量方法能大大提高信噪比较差时的不平衡信号提取精度。

为验证本文方案和原方案测量准确性、稳定性和重复性的差别，当左右校正面初始不平衡量低于150 mg时，在左校正面加385 mg(最小可达剩余不平衡量对应的试重)的试重，分别连续测量5次得到的结果如表2所示。

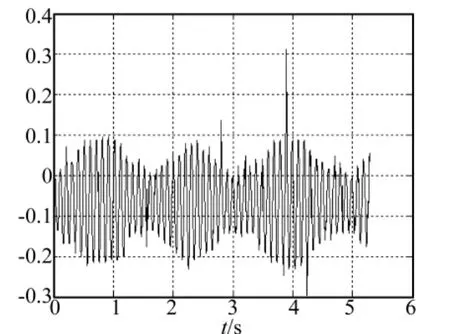
图3 带通滤波前振动信号波形Fig.3 Vibration signal waveform before Band－pass filter

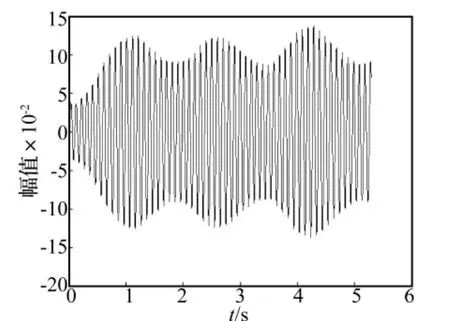
图4 带通滤波后振动信号波形Fig.4 Vibration signal waveform after Band－pass filter

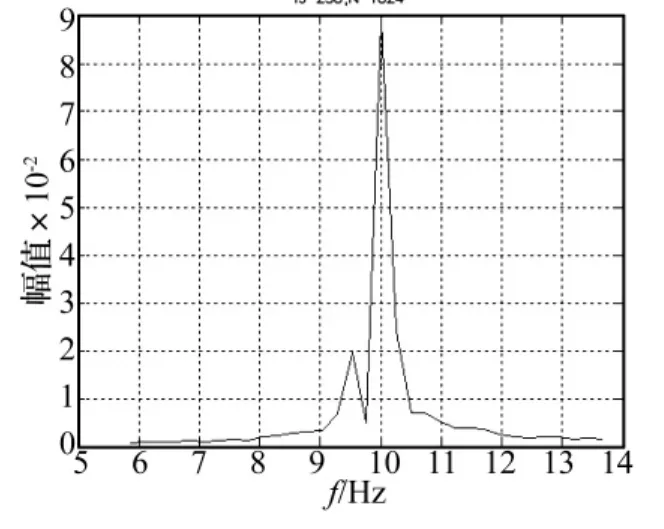
图5 FFT变换结果Fig.5 Result of FFT

从表2的实验结果可以看出，采用本文的信号处理方法后测试结果的准确性和重复性明显优于原方案，尤其是相位的稳定性大大改善，提高了小不平衡量测量的稳定性和可靠性，从而提高了动平衡测量系统的测量范围和测量精度。

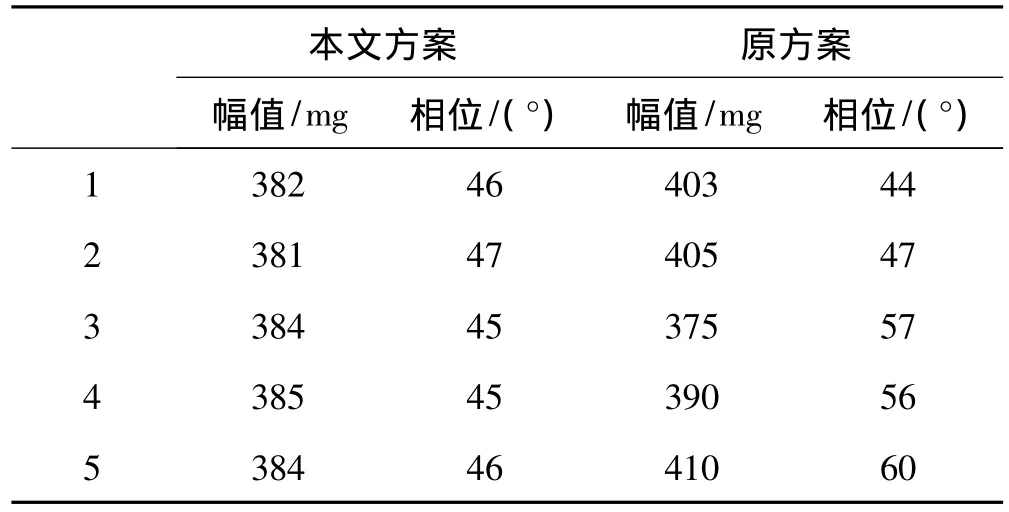
表2 5次测量结果对比Tab.2 Contrast of 5 times measurement

5 结论

提出了不平衡信号较小时由于机械或电测系统近频干扰引起的拍频现象，并且给出了一种存在拍频情况下准确提取不平衡信号的方法。采用FFT运算结果动态估计拍频周期，然后利用一个拍频周期内的数据作为训练样本，采用正弦逼近法提取不平衡信号的幅值和相位，该方法有效解决了不平衡量比较小时测量结果不稳定的现象，提高了测量精度。

采用本文的信号处理技术，开发了基于PC机的通用硬支承动平衡机测量系统，该测量系统已经配套于上海欧承动平衡机有限公司的HAB系列平衡机上，并在造纸和风机等行业的转子上成功应用。测试结果表明，该系统的最小剩余不平衡量低于0.3 g·mm/kg，赶上了国外同类产品的精度。

［1］陶利民，李 岳，温熙森.基于开关电容技术的信号跟踪滤波方法［J］.中国机械工程，2007，18(2):427－430.

［2］刘 健，潘双夏，杨克己，等.动平衡机用数字跟踪滤波器实现方法研究［J］.仪器仪表学报，2005，26(4):433 －436.

［3］杨克己，武二勇.高精度动平衡测量中自适应滤波技术应用研究［J］.仪器仪表学报，2005，26(1)，32 －35，58.

［4］盖建新，马怀俭，李延智，等.多通道动平衡测试系统算法［J］.电机与控制学报，2006，10(3):321 －323.

［5］商一奇，曹亦庆，柴艳丽，等.振动信号的幅值和相位计算方法分析［J］.计测技术，2010，30(4):30－32.

［6］张志新.智能动平衡仪自动量程的意义及实现［J］.风机技术，2003(4):57－59.

［7］孙 桥，于 梅.基于矢量合成的平衡机最小可达剩余不平衡度测试方法研究［J］.计量学报，2004，25(1):54－57.