极低频垂直偶极子在地-电离层中场的数值积分算法

彭怀云 陶 伟 潘威炎 郭立新

(1.西安电子科技大学理学院，陕西 西安 710071；2.中国电波传播研究所，青岛分所， 山东 青岛 266071；3.海军工程大学电子工程学院，湖北 武汉 430033； 4.海军装备研究院，北京 100161)

引 言

极低频(ELF)是指30 Hz以下频率范围的电磁波，波长范围为10 000 km至100 000 km以上与地球周长可比拟，可沿地-电离层空腔“绕行”几周，会出现“驻波”现象，在一些特定频率还将出现舒曼谐振，传播有别于超低频(SLF)以上频段。由于ELF电磁波能够渗透较深的地层，因此，在地质探测方面，可根据地面上ELF频段场强、相位以及表面阻抗随频率的变化，反演出接收点所在地域下面的地层导电率结构。由于ELF场强、相位、舒曼谐振频率对大范围低电离层电子浓度的变化较为敏感，对这些参数的研究可以分析出太阳风暴、地震等自然现象对低电离层的影响，对监测太阳风暴和地震的短临预报等方面具有重要意义。

自20世纪50年代以来，国内外学者对SLF及以下频段的传播开展了大量研究，主要有J. R. Wait[1]和J. Galejs[2]提出的地—电离层波导理论，以及Bannister提出的低频场强计算公式[3]。这些理论均对表征场强随传播距离变化的勒让德函数，Pν[cos(π-θ)],在ν<1的条件下(频率较高时)利用渐近式进行了近似，其适用范围为SLF频段和ELF频段的高频端，难以计算更低频率的ELF传播场。1999年Donald E. Barrick[4]提出了ELF垂直电偶极子在地—电离层腔体中的球谐级数算法，并针对地面和电离层都为理想导体的情况进行了计算分析。国内学者对此问题，利用球谐级数算法和时域有限差分法(FDTD)算法也进行了相关分析[5-6]，但这些方法收敛缓慢，计算效率不高。

鉴于上述情况，将分析ν<1时，勒让德函数Pν[cos(π-θ)]的直接积分计算方法，提出适于ELF频段地—电离层空腔传播的场强计算方法。

1. 理论分析

如图1所示的球坐标系，场源为位于θ=0，r=a+z0处的垂直电偶极子，地面和电离层理想化为位于r=a和r=a+h处的两个均匀反射壁，其导电率分别用σg和σi表示。场强观察点位于r=a+z处，取时谐因子为e-iωt，则在地-电离层空腔中传播的SLF及以下频段的场可表示为[7]

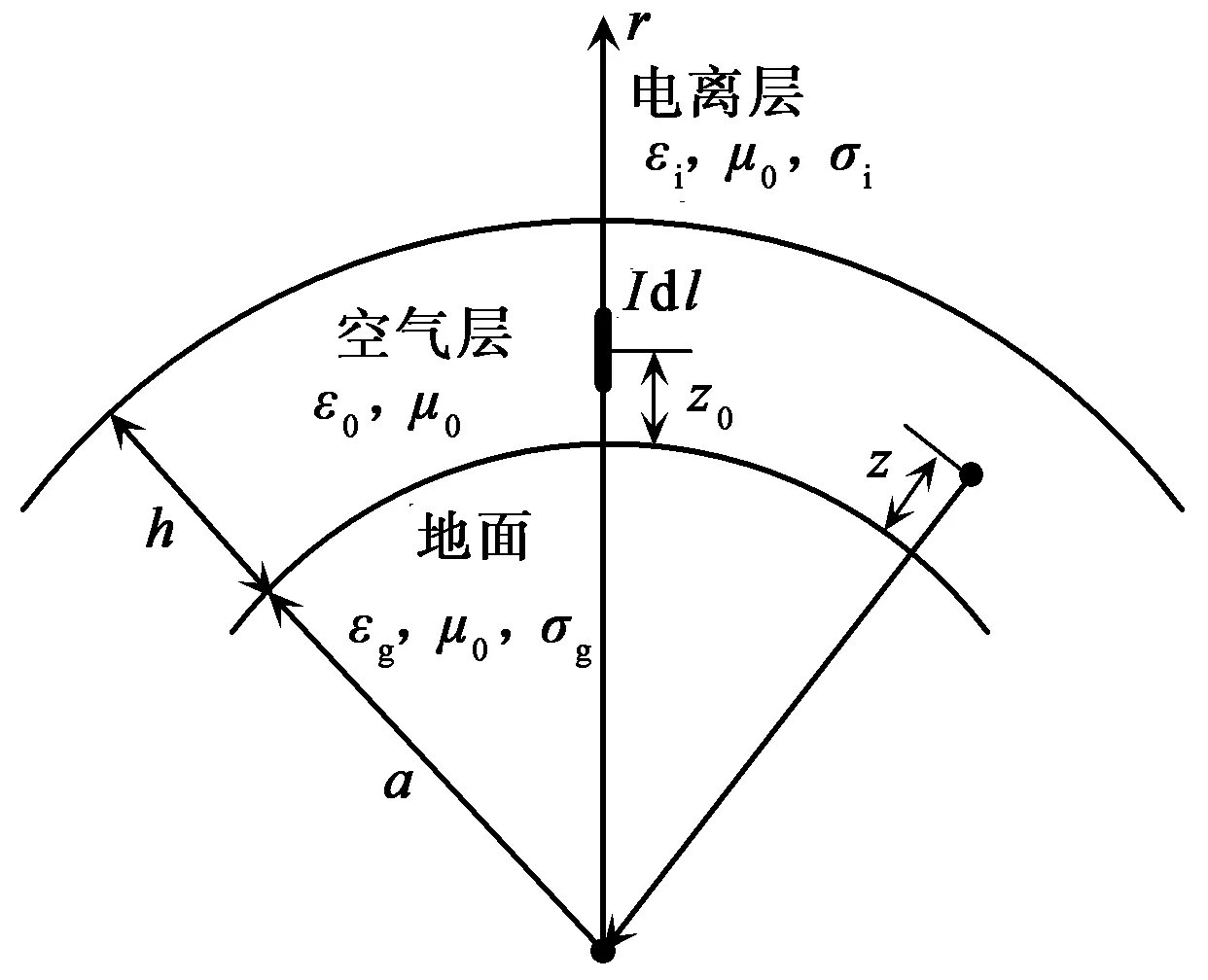
图1 地-电离层空腔模型

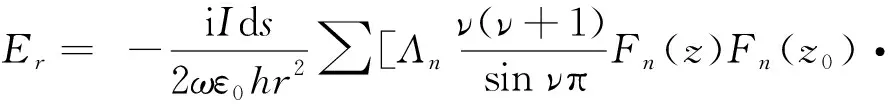
Pν(cos(π-θ))]

(1)

(2)

(3)

式中：

(4)

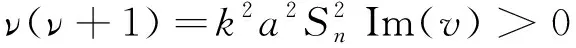
(5)

(6)

(7)

(8)

(9)

(10)

在ELF频段，Δi和Δg都很小，故存在近似

(11)

(12)

为便于后续分析计算，若令

(13)

利用公式

可得

(14)

则式(1)～(3)可改写为

Fn(z)Fn(z0)φ(ν,θ)]

(15)

(16)

(17)

式中：φ(ν,θ)的计算成为ELF在地-电离层空腔中传播计算的核心问题。以下工作为对φ(ν,θ)的计算研究。

2． φ(v,θ)的计算

根据参考文献[8]中的式(8.823)

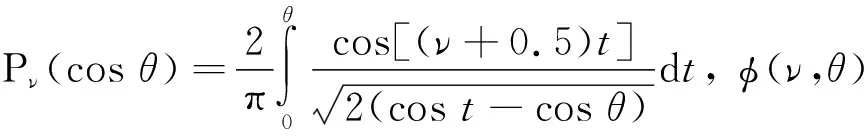
(18)

式中：

(19)

φ(ν,θ)的积分核函数在t=π-θ时存在奇点，可以分成两部分处理，即

φ(ν,θ)=I1+I2

(20)

式中：

(21)

I1可以利用梯形或辛普森数值积分法算出，令，π-θ-s=t,则I2可改写为

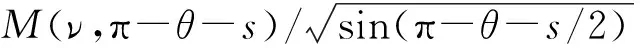
(22)

3. 计算分析与讨论

3.1 φ(ν,θ)的计算结果分析

除了本文中采用的计算方法外，φ(ν,θ)的计算还存在以下两种较为便捷的计算方法

1) Pν[cos(π-θ)]可展开为级数形式

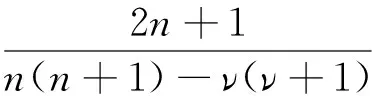
此方法可以计算ν为任意值时的φ1(ν,θ)，若选取地球半径a=6 370 km，电离层等效高度h=70 km,σg=10-3S/m,σi=10-5S/m,ν的实部和虚部随频率的变化如图2所示。

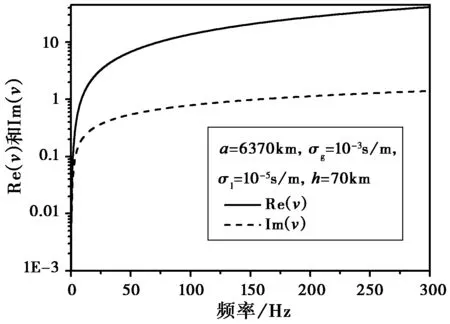
图2 的实部和虚部随频率的变化

为比较不同阶数求和对φ1(ν,θ)值的影响，选取n=100、200、500，此时20lg(φ1/φ)的变化情况，如图3所示。

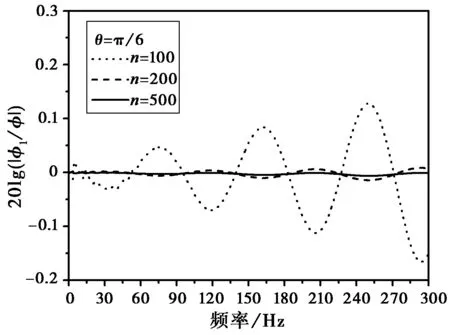
图3 不同求和阶数对计算精度的影响

由图3可以发现：随着n的增加，级数形式的计算结果与本文提出的直接积分计算方法结果逐渐接近；当ν≫1时，需取n>500才能获得高精度结果，Pν[cos(π-θ)]的级数形式方法在频率较低，ν较小时，具较高计算效率。

2) 当ν≫1，Im(ν)>0，θ<π时，存在如下渐近式[7]

利用图2所示的ν作为输入参数，计算f=10 Hz，30 Hz，100 Hz条件下的φ(ν,θ)、φ2(ν，θ)随θ的变化情况，如图4所示。从图4可以明显看出：频率越低，ν越小，φ(ν，θ)与φ2(ν，θ)的差异越大，即渐近式方法在频率较低情况下存在较大计算误差。

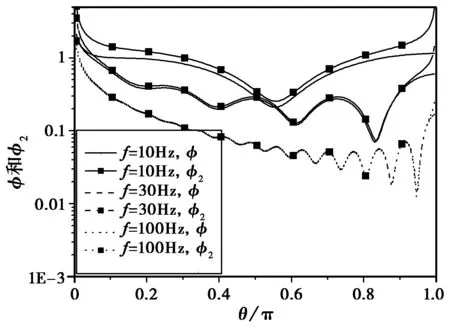
图4 不同频率φ与φ2的差异

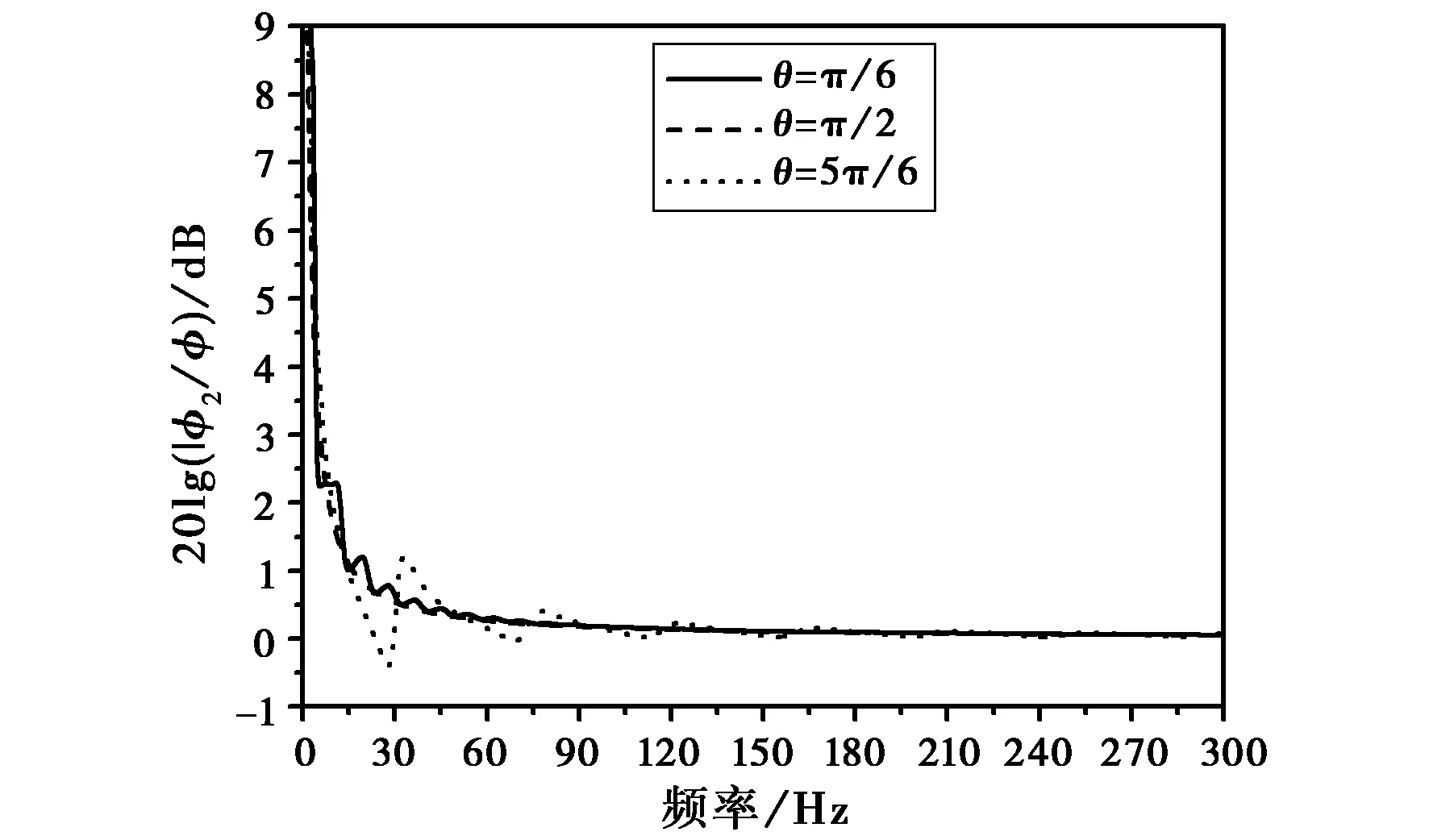
图5 指定θ时φ与φ2的差异随频率变化

当θ=π/6，π/2，5π/6时，渐近式计算方法与直接积分计算方法的差异如图5所示。可看出随着频率的降低，两种算法差异逐渐增加，频率在50 Hz以下差异可达0.5 dB以上，30 Hz以下差异达1 dB以上，5 Hz以下差异达6 dB以上。说明在ELF频段渐近式计算方法不适用。

数值积分计算方法相较于其他两种算法具有计算精度高、效率高的特点，适合于ELF频段的场强计算。

3.2 ELF场强计算分析

如图6～8所示，利用数值积分算法计算出频率f=1 Hz、3 Hz、5 Hz、10 Hz、20 Hz、30 Hz的ELF电磁波，在电离层等效高度h=70 km，地球半径a=6 370 km，地面导电率为σg=10-4S/m，电离层导电率为σi=10-5S/m条件下，场强随传播距离的变化。从中可以发现如下特点：

1) 经短大圆路径和长大圆路径传播的电波过对极点后相互叠加，产生“干涉”现象。频率越高，“干涉”现象产生的场强波动越“剧烈”，越靠近对极点，频率越低，“干涉”现象产生的波动越“舒缓”，场强波动谷值逐渐靠近源点；

2) 随着频率的降低，垂直偶极源产生的垂直电场分量Er变化相对平缓，当频率低至1 Hz以下，在1 000 km后场强近似趋于恒定。由于频率较低时，地-电离层空腔可传播模为横电磁波(TEM)模，其ν→0，则决定场强随传播距离变化的因子，Pν(cosθ(π-θ))→1,φ(ν,θ)→1/(νπ)，即场强随传播距离的变化较小，趋近恒定。物理解释为：在ELF频段，电波波长与地球周长可比拟，电波在地—电离层空腔中以“驻波”方式存在，在更低的1 Hz以下频段，电波波长可为地球周长的十几、几十倍，甚至更多倍，因此，其在几个地球周长内的不同路径的电波相位相差很小，总场接近于不同传播路径电场的同相叠加，因此“干涉”现象逐渐减弱直至消失，总场在远离源点时趋于基本恒定；

3) 水平电场Eθ和磁场Hφ随传播距离变得基本相似，由于采用球形对称模型，垂直电偶极子激励的水平电场Eθ和磁场Hφ在对极点将为0，所以在对极点附近Eθ和Hφ急剧下降。

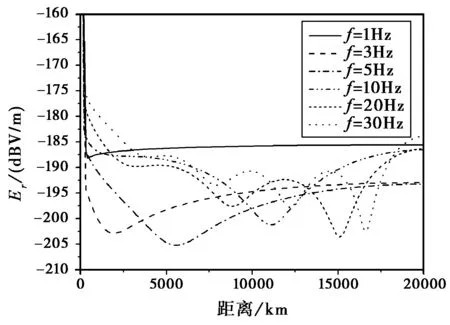
图6 垂直电场分量随传播距离变化

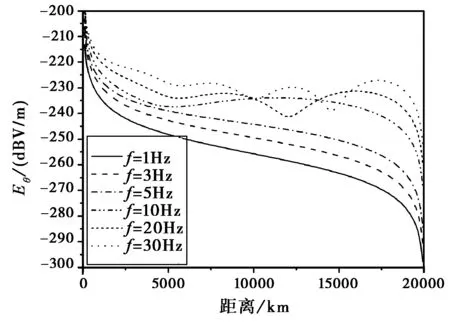
图7 水平电场分量随传播距离变化

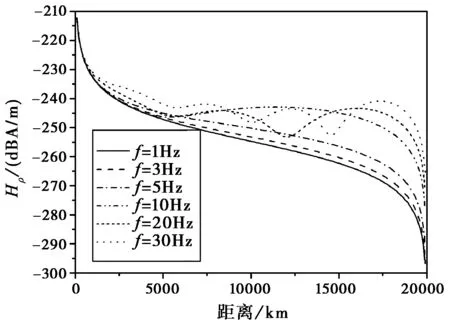
图8 水平磁场分量随传播距离变化

3.3 舒曼谐振计算分析

当选取电离层高度h=70 km，地、电离层为无损耗媒质(即地、电离层导电率为∞)时，在θ=π/6处，垂直电场分量Er随频率的变化如图9所示，在频率f=10.6 Hz、18.3 Hz、25.9 Hz处出现峰值。出现峰值的频率与文献[7]给出的无损耗腔体中的谐振频率完全一致，印证了本文算法的正确性和精度。

对于如图10所示的有耗媒质腔体，其谐振频率附近场强也存在峰值，但相较于无损耗媒质腔体场强变化相对“平缓”，且谐振频率也有所降低。结合图10、图11所示的不同电离层导电率、不同电离层等效高度的舒曼谐振频率变化情况，可以发现舒曼谐振频率对地、电离层的导电率变化较为敏感，存在如下规律：

1) 电离层导电率越高，即电子浓度越大，谐振频率越高；

2) 电离层等效高度越高，谐振频率越高。

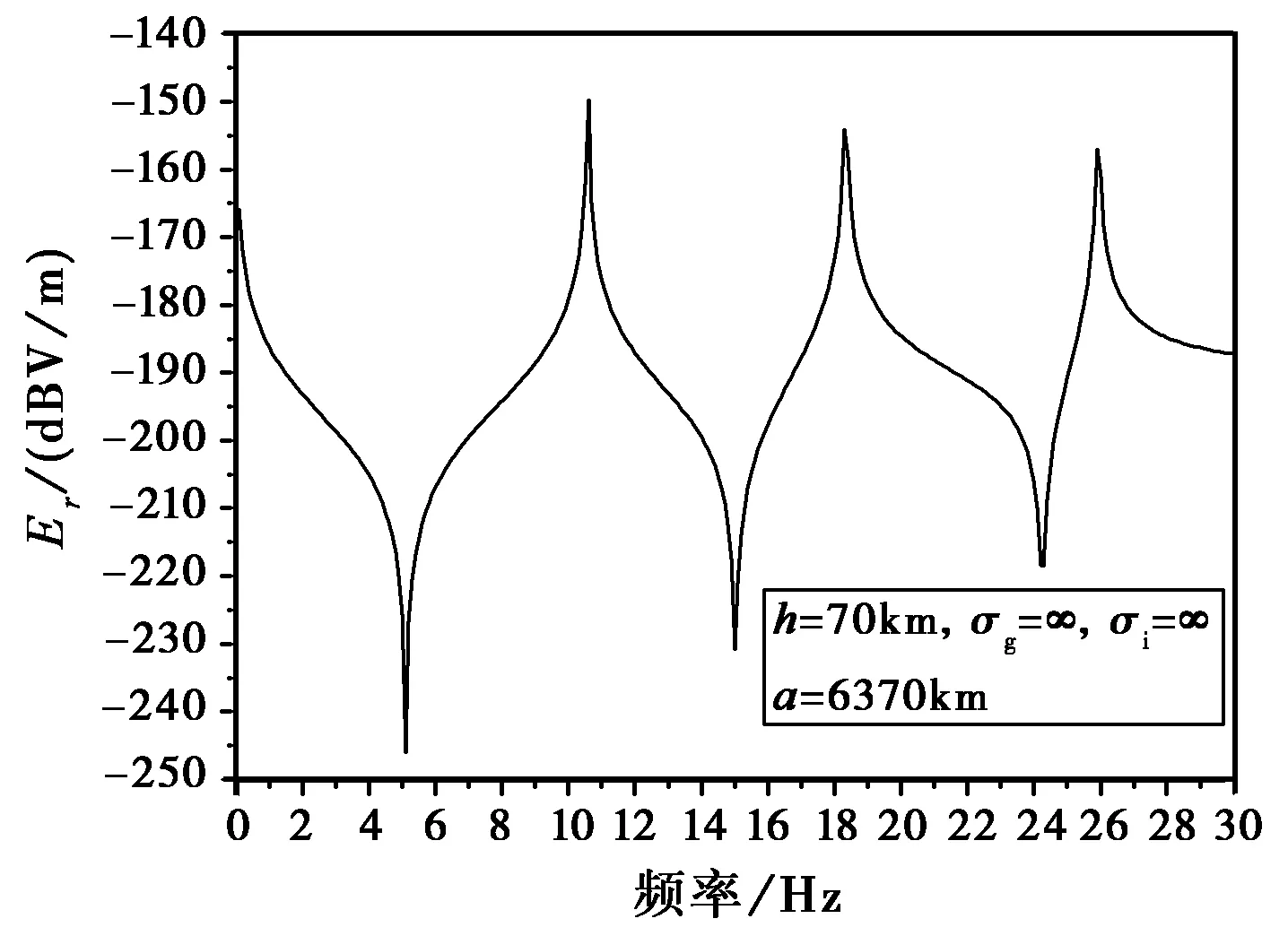
图9 无损耗腔体中谐振现象

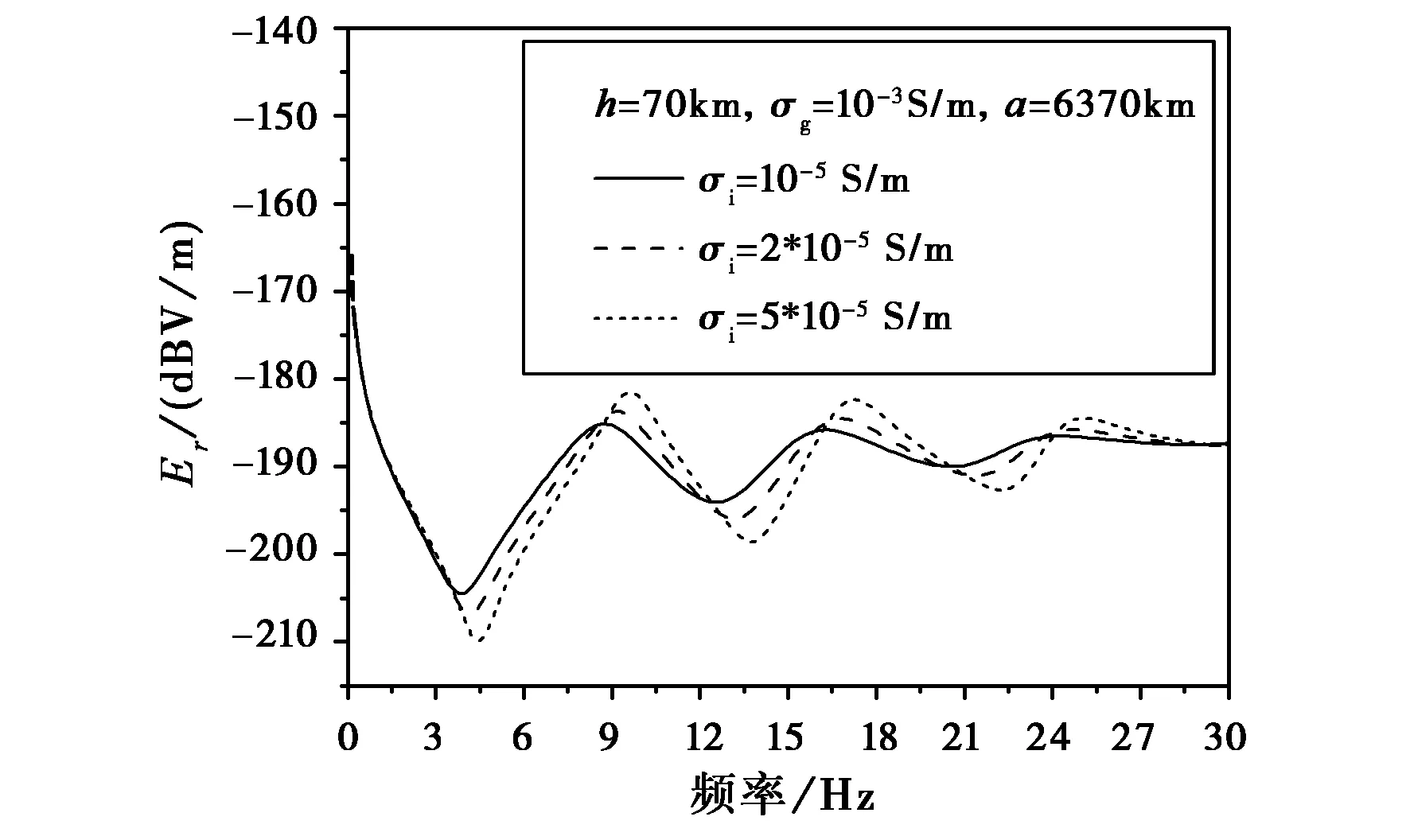
图10 不同导电率地-电离层腔体中谐振现象

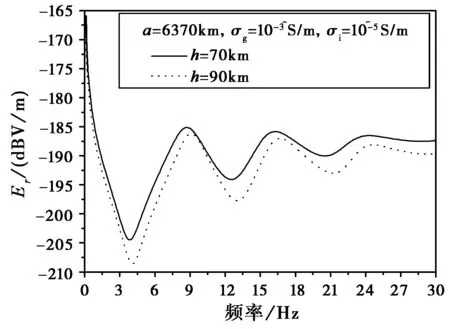
图11 不同电离层等效高度的谐振

4． 结 论

针对ELF电磁波在地—电离层空腔中的传播问题，采用直接积分法计算含有勒让德函数的Φ(ν,θ)，相比于渐近法和级数展开方法，具有计算精度高、效率高的特点。通过后续场强计算和舒曼谐振现象分析，认为数值积分方法更适合于ELF频段的场强计算。

[1] WAIT J R. Electromagnetic Waves in Stratified Media[M]. Class Reissue Edition. Piscataway: IEEE Press, 1996.

[2] GALEJS J. Terrestrial Propagation of Long Electromagnetic Waves[M]. Oxford: Pergamon Press, 1972.

[3] BANNISTER P R. Simplified formulas for ELF propagation at shorter distances[J]. Radio Science, 1986, 21(3): 529-537.

[4]BARRICK D E. Exact ULF/ELF dipole field strengths in the earth-ionosphere cavity over the schumann resonance region: idealized boundaries [J]. Radio Science, 1999, 34(1):209-227.

[5] 王元新, 樊文生, 潘威炎. 垂直电偶极子在地-电离层波导中场的球谐级数解[J]. 电波科学学报, 2007, 22 (2): 204-211.

WANG Yuanxin, FAN Wensheng, PAN Weiyan. Spherical harmonic series solution of fields excited by vertical electric dipole in earth ionosphere cavity[J]. Chinese Journal of Radio Science, 2007, 22 (2): 204-211.

[6] 董 慧, 闫玉波, 李清亮. FDTD模拟SLF/ELF水平电偶极子在非均匀地-电离层波导中的场[J]. 电波科学学报, 2010, 25(2): 366-370.

DONG Hui, YAN Yubo, LI Qingliang. FDTD analysis of fields excited by horizontal electric dipole in asymmetric earth-ionosphere cavity[J].Chinese Journal of Radio Science, 2010, 25(2): 366-370.(in Chinese)

[7] 潘威炎. 长波超长波极长波传播[M]. 成都: 电子科技大学出版社, 2004: 333-368.

[8] GRADSHTEYN I S, RYZHIK I M. Table of Integrals, Series, and Products[M]. New York: Academic Press, 1980.