双基地MIMO雷达发射波束形成与多目标定位

程院兵 顾 红 苏卫民

(南京理工大学电子工程与光电技术学院，江苏 南京 210094)

引 言

近年来，多输入多输出(MIMO)雷达[1-5]作为一种新体制雷达被广泛研究。它的发射/接收天线可根据系统要求灵活布置，并发射多个正交信号，从而实现空间分集和波形分集。根据发射/接收阵列的配置，MIMO雷达主要分为两类：统计MIMO雷达和单/双基地MIMO雷达。统计MIMO雷达的阵元间距较大，满足空间分集条件，通过从不同的角度观测目标以抑制其雷达截面积(RCS)闪烁，可获得较大的空间分集增益，提高探测性能[2]。单/双基地MIMO雷达的发射/接收阵元相距较近，不具有空间分集特性，但可利用波形分集技术在接收端形成大的虚拟孔径，具有提高角度分辨率和增加可检测目标数等优点[3-5]。

在双基地MIMO雷达目标定位中，目标的发射角(DOD)和接收角(DOA)是需要被估计的主要参数[6-9]。目前，估计这两个参数的方法主要有两类，第一类是基于二维谱峰搜索的算法[6-7]，这些算法在搜索范围较大，精度要求较高时，运算量巨大；第二类是基于子空间技术的算法[8-9]，如文献[8]利用匹配滤波输出数据的旋转不变特性，提出了一种基于ESPRIT谱估计的DOD和DOA估计算法，但需要额外的配对运算；文献[9]在文献[8]基础上提出了一种能够自动配对的算法，其运算量远小于二维搜索算法。然而，以上算法均利用发射波形的全分集特性，发射能量均匀分布在整个空域，降低了匹配滤波输出的信噪比(SNR)。众所周知，基于子空间技术的角度估计算法(如ESPRIT)对SNR敏感，角度估计精度随SNR增加而提高[10]。因此，可通过设计发射波束方向图，使发射能量聚焦的感兴趣的空域来提高匹配滤波输出的SNR，从而提高角度估计精度。目前，MIMO雷达的发射波束形成算法[11-13]大都基于各类优化算法，使发射波束方向图逼近某一期望的形状，然而这些算法在阵元数较多时运算量巨大。

本文提出一种子波束合成(SBS)算法用于双基地MIMO雷达发射波束形成。该算法通过对多个发射信号分别加权形成子波束，在空间叠加形成在感兴趣的空域具有恒定增益，在其它空域能量最小的发射波束，从而提高接收端信噪比。由于在发射端进行了加权处理，匹配滤波输出不再具有旋转不变特性，因此文献[9]的方法不再适用。经分析可知匹配滤波输出满足并行因子分解(PFD)模型，可用三阶张量表示。借鉴PFD在化学计量学中的应用[14]，本文结合角度恢复算法，提出一种基于PFD的目标定位算法，估计得到的目标DOD和DOA能自动配对。同时该算法避免了复杂的二维谱峰搜索、协方差矩阵估计和多次特征分解造成累积误差。仿真结果表明：利用本文提出的SBS算法和目标定位算法可有效提高双基地MIMO雷达的角度估计精度。

1. 阵列结构及信号模型

图1为本文采用的双基地MIMO 雷达的阵列结构。发射/接收天线阵列均为等间距均匀线阵，M和N分别表示发射和接收阵元数，dt和dr分别表示发射和接收阵元间距。s1(t)～sK(t)为K个正交的窄带发射信号，W=[w1,w2, …,wK]M×K为发射加权矩阵，图中wmk表示第k个权矢量wk的第m个元素。单点目标位于发射/接收阵列远场，θt和θr分别表示目标DOD和DOA.可以看出：通过对K个发射信号分别加权可形成K个子波束。

图1 双基地MIMO雷达阵列结构

假设感兴趣的发射角范围为Φ=[φ1,φ2]，我们的目的是设计W使K个子波束合成的总发射波束在Φ内具有恒定增益，而在其它空域发射能量最小。对任意时刻，各阵元的发射信号是K个发射信号的加权和，发射阵列的基带发射信号可表示为

(1)

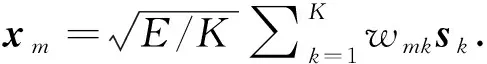
Yq=BΛqATX+Zq

(2)

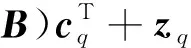
(3)

Y=[y1,y2, …,yQ]

=(A′⊕B)CT+Z

(4)

2. 发射波束形成

下面通过设计加权矩阵W使发射能量集中在感兴趣的发射角范围Φ内，而在其它范围最小。第k个波束在其指向角度φ的发射信号可表示为

(5)

定义空域能量比ηk为第k个波束在感兴趣的发射角范围Φ内的能量与整个发射角范围的能量比[15]，则

(6)

(7)

(8)

P(θt)=aH(θt)Rta(θt),θt∈Φ=[φ1,φ2]

(9)

式中：a(θt)=[1, egtsin(θt), …, egt(M-1)sin(θt)]T；Rt=XXH=E/K·WWH为发射信号互相关矩阵。可以看出该算法是通过对多个发射信号分别加权形成子波束，在空间叠加使发射能量聚焦在感兴趣的空域，称之为子波束合成(SBS)算法。为了能够获取宽的接收角探测范围，在接收端处理时未形成波束。接收端波束形成方法可借鉴相控阵雷达中的方法形成窄波束，也可采用类似本文发射端波束形成算法形成具有一定宽度的矩形波束。

3. 多目标定位

由于在发射端进行了加权处理，匹配滤波输出不再具有旋转不变特性，文献[9]的方法不再适用。并行因子分解(PFD)被广泛应用于心理测试学和化学计量学等领域[14,17-18]。给出一种基于PFD的目标定位算法。

可以看出式(4)是一个并行因子模型，可用三阶张量y∈K×N×Q表示。根据三阶张量的并行因子分解定义[14]可将y分别按三个不同维方向分解为以下三个等效矩阵

(10)

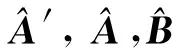
(11)

其中：步骤1～3为基于ALS算法的标准PFD，步骤4为基于谱估计的目标DOD和DOA恢复算法。

4. 仿真结果与性能分析

假设雷达工作载频f0=10 GHz，发射和接收阵元数均为M=N=12，发射和接收阵元间距均为半波长。感兴趣的发射角范围Φ=[-5°,5°]，根据式(8)可选取发射信号数K=3(ρ=99.97%)。发射信号为三个正交的带宽为50 MHz的窄带Hadamard编码信号，每个脉冲内编码数L=256，脉冲数Q=100.假设相参处理间隔内，目标反射系数服从Swerling-II模型[21]，即在脉冲内保持不变，脉冲间随机波动。基于PFD的目标定位算法中取εTh=10-6，步骤4中采用Root-MUSIC谱估计算法[19]恢复目标角度。从发射波束方向图、目标估计角度星座图和测角均方根误差三个方面说明本文提出的发射波束形成算法和目标定位算法的优越性。

实验1：根据发射角范围Φ计算矩阵AΦ，对其进行特征值分解得到最大的三个特征值对应的特征向量w1，w2,w3,得到加权矩阵W，根据式(9)即可得到发射波束方向图。图2(a) 给出了SBS算法形成的三个子发射波束方向图，子方向图1, 2, 3分别与权矢量w1,w2,w3对应。图2(b) 给出了总发射波束方向图，同时给出了传统MIMO雷达的发射波束方向图。可以看出：传统MIMO雷达由于全向发射，能量均匀分布在整个空域，而SBS算法形成的发射波束方向图在感兴趣的发射角范围内具有恒定增益，其增益比传统MIMO雷达高约6 dB.

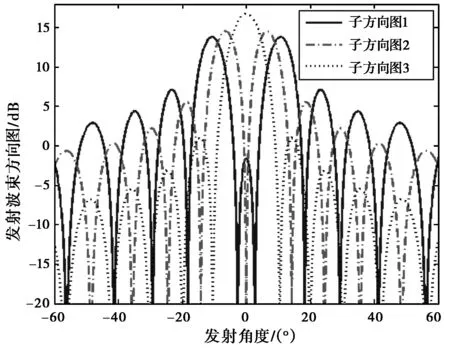
(a) 子发射波束方向图

(b) 总发射波束方向图图2 SBS算法形成的发射波束方向图

实验2：存在三个目标，其信噪比均为-8 dB，发射/接收角度分别为(θt1,θr1)=(-3°, 0°), (θt2,θr2)=(0°, 10°), (θt3,θr3)=(2°, 8°)，其中目标2和目标3角度邻近。图3给出了传统MIMO雷达采用文献[9]算法和本文提出的SBS算法结合基于PFD的定位算法得到的目标估计角度星座图。Monte Carlo实验次数为200.可以看出，文献[9]算法对目标2和目标3的测角出现很大误差。与其相比，本文算法可同时估计三个目标DOD和DOA，实现多目标定位，且具有更高的定位精度。

实验3：计算三个目标在不同信噪比下的测角均方根误差，目标角度与实验2相同。均方根误差定义为

(a) 文献[9]算法

(b) SBS算法结合基于PFD的定位算法图3 目标估计角度星座图

图4 测角均方根误差

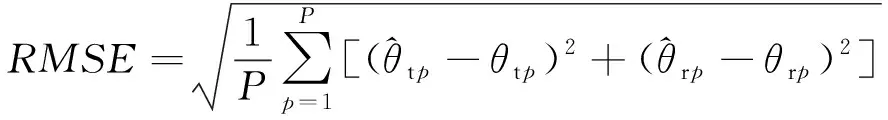
以上实验充分说明本文提出的子波束合成算法能有效地将发射能量聚焦在感兴趣空域，提高匹配滤波输出信噪比，同时提出的基于PFD的目标定位算法可联合估计目标DOD和DOA，二者自动配对，同时避免了二维谱峰搜索、协方差矩阵估计和多次特征分解造成累积误差，从而具有更高的测角精度。

5. 结 论

在双基地MIMO雷达阵列结构和信号模型基础上，提出一种子波束合成算法用于发射波束形成，使发射能量聚焦在感兴趣的空域，从而缓解了传统双基地MIMO雷达全向发射造成信噪比损失的问题，且算法简单，设计的波束灵活性高。同时，本文提出的基于PFD的目标定位算法避免了复杂的二维谱峰搜索和协方差矩阵估计，消除了多次特征分解造成的累积误差，估计得到的目标DOD和DOA能自动配对，无需额外配对运算。仿真结果表明，与文献[9]方法相比，本文算法可有效提高双基地MIMO雷达的目标定位精度。

[1] LI J, STOICA P. MIMO radar signal processing[M]. New York: Wiley Press, 2008.

[2] HAIMOVICH A, BLUM R, CIMINI L. MIMO radar with widely separated antennas[J]. IEEE Signal Processing Magazine, 2008, 25(1): 116-129.

[3] LI J, STOICA P. MIMO radar with collocated antennas[J]. IEEE Signal Processing Magazine, 2007, 24(5): 106-114.

[4] 曾建奎, 何子述. 慢起伏目标的多输入多输出雷达检测性能分析[J]. 电波科学学报, 2008, 23(1): 159-161.

ZENG Jiankui, HE Zishu. Analysis of MIMO detection performance for slow fluctuating target[J]. Chinese Journal of Radio Science, 2008, 23(1): 159-161. (in Chinese)

[5] 刘志国, 廖桂生. 双基地MIMO雷达互耦校正[J]. 电波科学学报, 2010, 25(4): 663-667.

LIU Zhiguo, LIAO Guisheng. Mutual coupling calibration for bistatic MIMO radar systems[J]. Chinese Journal of Radio Science, 2010, 25(4): 663-667. (in Chinese)

[6] XU L, LI J, STOICA P. Target detection and parameter estimation for MIMO radar systems[J]. IEEE Transactions on Aerospace and Electronic Systems, 2008, 44(3): 927-939.

[7] YAN H D, LI J, LIAO G S. Multi-target identification and localization using bistatic MIMO radar systems[J]. EURASIP Journal on Advances in Signal Processing, 2008, 8(2): 1-8.

[8] CHENG D F, CHENG B X, QIN G D. Angle estimation using ESPRIT in MIMO radar[J]. Electronics Letters, 2008, 44(12): 770-771.

[9] CHEN J L, GU H, SU W M. A new method for joint DOD and DOA estimation in bistatic MIMO radar[J]. EURASIP Journal on Advances in Signal Processing, 2010, 90(2): 714-718.

[10] 王永良, 陈 辉, 彭应宁, 等. 空间谱估计理论与算法[M]. 北京:清华大学出版社, 2004.

WANG Yongliang, CHEN Hui, PENG Yingning, et al. Spatial spectrum estimation theory and algorithm[M]. Beijing: Tsinghua University Press, 2004. (in Chinese)

[11] FUHRMANN D R, SAN ANTONIO G. Transmit beamforming for MIMO radar system using signal cross-correlation[J]. IEEE Transactions on Aerospace and Electronic Systems, 2008, 44(1): 171-186.

[12] 胡亮兵, 刘宏伟, 杨晓超, 等. 集中式MIMO雷达发射方向图快速设计方法[J]. 电子与信息学报, 2010, 32(2):481-484.

HU Liangbing, LIU Hongwei, YANG Xiaochao, et al. Fast transmit beampattern synthesis for MIMO radar with collocated antennas[J]. Journal of Electronics and Information Technology, 2010, 32(2): 481-484. (in Chinese)

[13] 刘韵佛, 刘 铮, 谢 容. 一种基于拟牛顿法的MIMO雷达发射方向图综合方法[J]. 电波科学学报, 2008, 23(6): 1188-1193.

LIU Yunfo, LIU Zheng, XIE Rong. Transmit pattern synthesis algorithm for MIMO radar based on Newton-like method[J]. Chinese Journal of Radio Science, 2008, 23(6): 1188-1193. (in Chinese)

[14] BRO R. PARAFAC: tutorial and applications[J]. Chemometrics and Intelligent Laboratory Systems, 1997, 38(2): 149-171.

[15] TRESS V H L. Optimum array processing[M]. New York: Wiley Press, 2002.

[16] FORSTER P, VEZZOSI G. Application of spheroidal sequences to array processing[C]// Proceedings of IEEE internal conference Acoustics, Speech, and Signal Processing, Dallas, TX, May 1987: 2268-2271.

[17] SIDIROPOULOS N D, GIANNAKIS G B, BRO R. Blind PARAFAC receivers for DS-CDMA systems[J]. IEEE Transactions on Signal Processing, 2000, 48(3): 810-823.

[18] TOMASI G, BRO R. A comparison of algorithms for fitting the PARAFAC model[J]. Computational Statistics and Data Analysis, 2006, 50(7): 1700-1734.

[19] STOICA P, MOSES R. Introduction to spectral analysis[M]. New Jersey: Prentice-Hall, 1997.

[20] LIU S Z, TRENKLER G. Hadamard, khatri-rao, kronecker and other matrix products[J]. International Journal of Information and Systems Sciences, 2008, 4(1): 160-177.

[21] 丁鹭飞, 陈建春. 雷达原理[M]. 北京: 电子工业出版社, 2009.