二维海面上方金属目标复合散射快速算法研究
姬伟杰 童创明,2
(1.空军工程大学导弹学院,陕西 三原 713800;2.毫米波国家重点实验室,江苏 南京 210096)
引 言
目标与随机地海面的复合电磁散射研究在军用和民用领域都有广泛的应用,引起了国内外学者的极大关注,但是大多数研究都侧重于二维散射问题[1-6]。对于在实际中遇到的三维散射问题研究则比较少,而且大多采取解析法来求解以降低计算复杂度[6-7]。解析法对于粗糙面参数有严格的适用范围,不能用于计算复杂参数粗糙面与目标的复合散射,同时不能得到交叉极化的结果。数值算法不受此限制,因此,研究求解实际地海面与目标复合散射的快速数值算法具有重要意义。
在二维粗糙面与目标的复合散射计算中,不仅要考虑目标与粗糙面自身的散射,还要考虑它们之间的相互作用,而其中粗糙面的未知量占绝大多数。因此,如何快速有效地计算粗糙面的电磁散射是一个重要的问题。以往的方法都是将目标与地海面当作整体来建模以及求解[8-11],由于数值算法都要产生矩阵方程,这就导致矩阵数据量过大而不能快速求解。N.Dechamps 等提出了一种计算一维分层粗糙面的快速数值算法:层内波传播展开法[12](PILE),将通过矩量法(MoM)得到的线性方程组求解分成四步来迭代求解:两步用来求解单层粗糙面自身的散射;两步用来求解上层粗糙面与下层粗糙面之间的相互作用。Kubicke G等进一步将其扩展应用于计算粗糙海面上方金属目标的复合电磁散射特性[13]。
推导了二维粗糙面上方目标复合散射的耦合积分方程组,将PILE算法扩展应用于求解该积分方程组。PILE的优点就是将目标与粗糙面的散射分开来考虑,因此,粗糙面的表面积分方程可以用已经成熟的快速数值算法来求解,如稀疏矩阵平面迭代及规范网格法(SMFSIA/CAG)[14],它所需内存小、计算速度快,是一种计算二维导体粗糙面电磁散射的有效快速数值算法。而目标的未知量较小,其表面积分方程可以采用传统的基于三角屋顶(RWG)基函数的MoM来求解[15]。
利用该算法计算了具有PM海浪谱的海洋粗糙面上方各种典型目标的复合双站散射系数,通过与传统MoM的结果相比较,验证了算法的有效性,讨论了算法的收敛性。计算了海面上导弹目标的双站散射系数(BSC)。该算法提供了一种计算二维粗糙面上方目标复合电磁散射的有效途径。
1.基础理论
1.1 耦合积分方程组
图1所示为二维随机海洋粗糙面上方金属目标的散射,ki与ks分别为入射与散射方向矢量,θi与φi为入射角,θs与φs为散射角,H为目标距离海面高度,粗糙面的高度函数z=ζ(x,y),且〈ζ(x,y)〉=0.

图1 海面上导体目标示意图
当粗糙面上没有目标时,满足磁场边界积分方程(MFIE):
n′×Hs(r′)ds′
(1)
式中:Hinc(r)为入射磁场;n为粗糙面表面法向量;S指粗糙面表面;g(r,r′)=(r-r′)G(R),
自由空间中的金属目标满足电场边界积分方程(EFIE)


Hb(r′)))]g(r,r′)ds′
(2)
式中:Einc(r)为入射电场;nb为目标表面法向量;Sb指目标表面;k0为自由空间波常数; μ0为区域内磁导率。
当目标与粗糙面同时存在时,必须考虑目标与粗糙面的相互作用,由等效电流原理,粗糙面对目标的散射贡献为

(3)
式中:Js(r)=n×Hs(r),表示粗糙面表面电流;ε0为区域内介电常数。
目标对粗糙面的散射贡献为

(4)
式中:Jb(r)=nb×Hb(r),表示目标表面电流。
结合式(1)和(2),可以得到目标与粗糙面的耦合积分方程组为

(5a)


(5b)
1.2 E-PILE+SMFIA/CAG算法
将式(5)看成一个整体,直接运用MoM可以得到如下线性方程组
ZI=V
(6)
式中:Z为总的阻抗矩阵,它既包括粗糙面的阻抗矩阵,又包括目标的阻抗矩阵,以及目标与粗糙面之间的相互作用阻抗矩阵,维数为2(N+M)×2(N+M)(N为粗糙面表面的未知量,M为目标表面的未知量);I为所求未知向量为
(7)
上标T表示转秩,Ir表示粗糙面的未知向量;V为激励向量,包括目标的激励向量Vo和粗糙面的激励向量Vr为
(8)
为了有效地求解线性方程组,将阻抗矩阵Z分成四块
(9)
式中:Zo表示目标自身的阻抗矩阵;Zr表示单层粗糙面自身的阻抗矩阵;Zo→r与Zr→o表示粗糙面与目标相互作用的阻抗矩阵。对阻抗矩阵Z求逆可得
(10)
式中:
T=(Zo-Zr→o(Zr)-1Zo→r)-1
(11a)
U=-(Zo-Zr→o(Zr)-1Zo→r)-1Zr→o(Zr)-1
(11b)
Q=-(Zr)-1Zo→r(Zo-Zr→o(Zr)-1Zo→r)-1
(11c)
W= (Zr)-1+(Zr)-1Zo→r(Zo-Zr→o(Zr)-1Zo→r)-1×
Zr→o(Zr)-1
(11d)
所求未知向量I为
(12)
结合式(8)和式(9),可以得到粗糙面未知向量
Io=(Zo-Zr→o(Zr)-1Zo→r)-1(Vo-Zr→o(Zr)-1Vr)
= (I-(Zo)-1Zr→o(Zr)-1Zo→r)-1(Zo)-1×
(Vo-Zr→o(Zr)-1Vr)
I为单位矩阵,定义特征矩阵为
Mc=(Zo)-1Zr→o(Zr)-1Zo→r
(13)
则由矩阵级数的求和理论,当Mc为收敛矩阵时,有
(14)
数值计算中,矩阵的阶数必须适当的截断,定义截断阶数为pPILE,结合式(12)和(14)可得
(15)
式中:
(16)

1.3 锥形入射波与散射系数
为避免人为截断粗糙面引起的边缘效应,采用锥形波入射[14],限于篇幅,本文只考虑水平极化入射波情况,表达式为

ikzz)·ETE(kx,ky)h(-kz)
(17)

ikzz)·ETE(kx,ky)e(-kz)
(18)

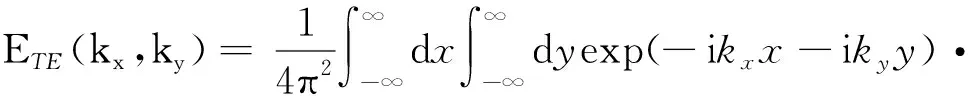
exp(i(kixx+kiyy)(1+w))exp(-t)
(19)
其中
t=tx+ty=(x2+y2)/g2
g参数控制锥形入射波的宽度。
定义双站散射系数
(20)

2.数值分析
2.1 算法的有效性与收敛性验证
采用具有PM海浪谱的随机粗糙面模拟实际海洋面[16]。PM谱是以风速为参量充分成长状态的海浪频谱,是由观测得到的纯经验谱,三维PM谱具有如下形式
(21)
定义迭代误差
(22)
式中:Ztotal表示总的阻抗矩阵,它既包括粗糙面的阻抗矩阵,又包括目标的阻抗矩阵;p表示阶数。
以海洋粗糙面上方的金属球体(见图2)为例,验证算法的有效性。球体位于海面的正上方,球心距离海面高度为H,海面大小为Lx×Ly=10λ×10λ,风速U19.5=5 m/s,此时海面方差h=0.133 4 m.入射波波长取λ=1 m,入射角θi=30o,φi=0o,φv=0,锥形波参数g=Lx/3.海面剖分密度为每平方波长上64个采样点,产生6 400个采样点,12 800个未知数,强作用距离rd=2.5λ.如无特殊说明,文中所有结果均是对相同参数粗糙面实现10次取平均的结果。图3所示为球体半径取0.5λ,高度H=1.0λ,p取不同数值时实现一次的散射系数,同时给出了误差大小,并与运用传统MoM得到的结果进行了对比。由图3可知,随着p的增大,误差迅速减小,当p=2时两种方法结果完全吻合。

图2 海面上方的金属球体
验证算法的收敛性。其他参数不变,目标分别取半径为0.5λ的球体、圆柱(底面半径为0.5λ,高为1λ)、边长为1λ的立方体,目标表面剖分的三角面元个数分别为1 038、1 485和1 884,距离海面高度H=1.0λ,目标尺寸相对于粗糙面的尺寸比较小(约为1: 100),近似等效于目标与无限大粗糙面之间的相互作用,此时,目标可认为是平面波入射。图4所示为由式(22)计算相应的迭代误差随阶数p的变化结果,由图可知,随着阶数p的增大,误差成指数级衰减速度,且目标为球体时收敛速度最快,目标为立方体时收敛速度最慢,这是由于立方体目标体积较大,与海面相互作用较强造成的,但所有结果均满足计算精度要求,证明了本文算法对任意形状目标都具有良好的收敛性。计算所需时间见表1,可以发现,与MoM相比,E-PILE+SMFIA/CAG计算时间大大减少。
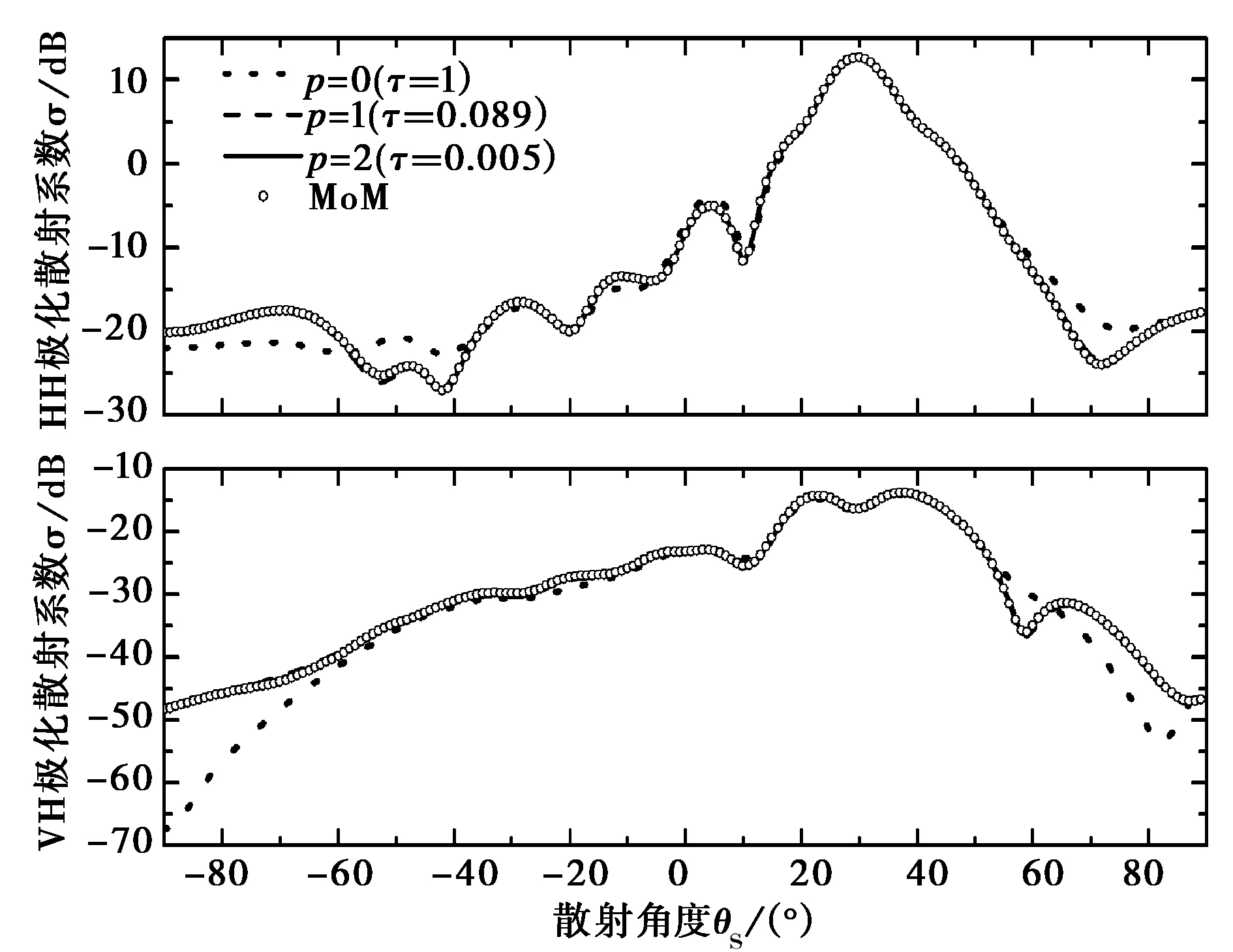
图3 算法的验证

图4 迭代误差变化趋势
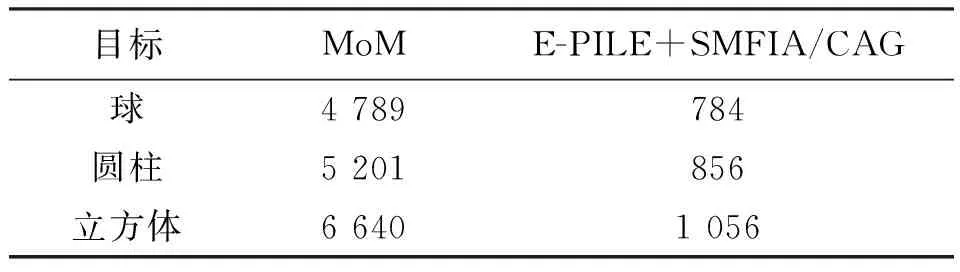
目标MoME-PILE+SMFIA/CAG球4 789784圆柱5 201856立方体6 6401 056
2.2 结果分析与讨论
计算海面上方金属球体的双站散射系数,球体半径R=0.5λ,高度H=1.0λ,收敛精度取τ≤1%(对应pPILE=2)。图5(a)给出了HH和VH极化散射系数随方位角θs变化情况,图中还给出了只有海面时的散射系数,海面上方有无目标时HH极化和VH极化散射系数在镜面放射方向均有峰值,当海面上方有目标时,散射系数在除镜面方向外的角度范围内明显增大,尤其在后向散射方向更为明显,同时由图可知,VH极化散射系数要比HH极化散射系数小两个数量级。HH和VH极化散射系数随方位角φs的变化见图5(b)(θs=θi=30°),由图可知,海面上有目标时,HH极化散射系数在20°~160°范围内增大,在90°~150°范围内变化最为明显,VH极化散射系数在所有角度都增大。

(a) 散射系数随高低角变化(φs=0°)

(b) 散射系数随方位角变化(θs=30°)图5 海面上球体散射系数
其他参数不变,令pPILE=4,图6(a)和图6(b)分别是海面上目标为圆柱和立方体时的散射系数,其中圆柱参数:底面半径为0.5λ,高为1λ,立方体边长为1λ.结合图5(a)可知,当目标为立方体时散射系数最大,目标为圆柱时次之,当目标为球时散射系数最小,但都明显强于无目标时海面的散射系数。这是由于立方体体积最大,与海面的相互作用较强。因此,当海面上方目标为立方体时散射系数变化最明显,球体积最小,与海面的相互作用较小;当目标为球时散射系数变化最小。由此可知,海面上有目标时的散射系数明显大于无目标时的散射系数,它们之间的差异正体现了目标与粗糙面的相互作用,并且它们之间的相互作用随目标体积的增大而增强。同时由图可知,当海面上方有目标时VH极化散射系数变化比HH极化散射系数变化明显,这对地海面背景中目标的探测与识别具有一定的理论指导意义。

(a) 海面上方圆柱散射系数
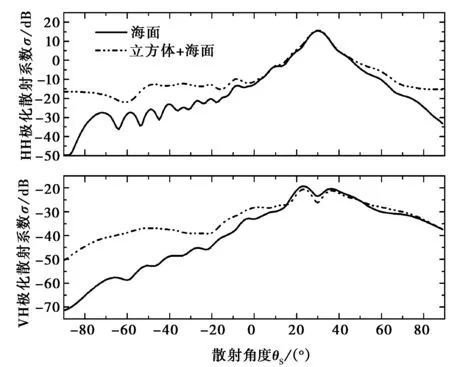
(b) 海面上方立方体散射系数图6 海面上目标散射系数
讨论海面上方存在复杂目标的情况。海面上方目标为导弹模型(如图1所示),导弹模型见图7,长度为4.9 m,弹体半径为0.25 m,翼展为2 m.海面大小取Lx×Ly=40λ×40λ,剖分密度为每平方波长上64个采样点,产生102 400个采样点,204 800个未知数,为保证导弹与海面充分相互作用,取pPILE=5,其余参数不变。导弹距离海面高度分别取1λ、5λ和10λ,入射波从导弹头部入射时散射系数如图8(a)所示,此时入射角为φi=90°,入射波从导弹侧面入射时(φi=0°)散射系数见图8(b).由图可知,随着导弹距离海面高度增大,目标与海面之间相互作用减小,除镜面方向外,在其余角度散射系数均逐渐变小。

图7 导弹模型示意图

(a) 入射波头部入射(φi=90°)

(b) 入射波头部入射(φi=0°)图8 不同目标高度对应的散射系数
研究海面上风速对散射系数的影响。其他参数不变,导弹距离海面高度为5λ,海面上19.5 m处风速分别取3 m/s、5 m/s和7 m/s,相应的散射系数如图9所示,其中图9(a)是入射波从导弹头部(φi=90°)入射的情况,图9(b)是入射波从导弹侧面(φi=0°)入射的情况。由图可知,随着海面上风速增大,海面粗糙度增大,镜面散射逐渐减弱而漫散射增强,因此,镜面方向散射系数减小,而其余角度散射系数均有所增强,VH极化表现的更为明显。同时由图可知,同图8结果相似,入射波从侧面入射时的散射系数明显大于入射波从头部入射时的情况,这是由于入射波从导弹侧面入射时的雷达照射面积远大于从头部入射时的情况。

(a) 入射波头部入射(φi=90°)

(b) 入射波侧面入射(φi=0°)图9 不同海面风速对应的散射系数
3. 结 论
结合SMFIA/CAG与基于RWG基函数的MoM,运用迭代数值法快速计算了二维粗糙面上方三维金属目标的复合散射系数。该算法基于物理散射机理,理论简明,易于编程实现,并且不受粗糙面与目标参数限制,可以计算复杂目标与粗糙面的复合散射,是一种计算二维粗糙面上方目标的复合电磁散射的快速有效算法。
结合PM谱的海洋粗糙面,应用该算法计算了海面上方典型目标的散射系数,验证了算法的有效性,讨论了算法的收敛性。结果表明:当海面上方有目标时散射系数明显大于没有目标时的情况。最后,运用该算法计算了海面上导弹目标的复合散射系数,并讨论了目标高度以及海面上风速对散射系数的影响,结果表明:随着目标高度增加,散射系数逐渐减小,随着海面上风速增大,镜面散射减小而漫反射增强。
[1] WANG X, WANG C F, GAN Y B, et al. Electromagnetic scattering from a circular target above or below rough surface[J]. PIER, 2003, 40: 208-226.
[2] 王 蕊, 郭立新, 王安琪. 不同土壤类型的粗糙地面与其下方埋藏目标复合电磁散射研究[J]. 物理学报, 2010, 59(5): 3179-3186.
WANG Rui, GUO Lixin, WANG Anqi. Investigation of electromagnetic scattering interaction between the buried target and the rough surface in different types of soil[J]. Acta Physica Sinica, 2010, 59(5): 3179-3186. (in Chinese)
[3] KUBICKE G, BOURLIER C, SAILLARD J. Scattering from canonical objects above a sea-like one-dimensional rough surface from a rigorous fast method[J]. Wave in Random and Complex Media, 2010, 20(1): 156-178.
[4] 姬伟杰, 童创明. 分层粗糙面下方介质目标散射的快速算法[J]. 电波科学学报, 2010, 25(2): 336-342.
JI Weijie, TONG Chuangming. Fast calculation of EM scattering from layered rough surfaces with buried dielectric target[J]. Chinese Journal of Radio Science, 2010, 25(2): 336-342. (in Chinese)
[5] JOHNSON J T. A study of the four-path model for scattering from an object above a halfspace[J]. Microw Opt Technol Lett, 2001, 30(7): 130-134.
[6] 郭立新, 王运华, 吴振森. 二维导体微粗糙面与其上方金属平板的复合电磁散射研究[J]. 物理学报, 2005, 54(11): 5130-5138.
GUO Lixin, WANG Yunhua, WU Zhensen. Electromagnetic scattering interaction between a conducting plate and a 2-D conducting slightly rough surface[J]. Acta Physica Sinica, 2005, 54 (11): 5130-5138. (in Chinese)
[7] 叶红霞, 金亚秋. 三维随机粗糙面上导体目标散射的解析-数值混合算法[J]. 物理学报, 2008, 57(2): 839-846.
YE Hongxia, JIN Yaqiu. A hybrid analytical-numerical algorithm for scattering from a 3-D target above a randomly rough surface[J]. Acta Physica Sinica, 2008, 57 (2): 839-846. (in Chinese)
[8] DENG Fangshun, HE Siyuan, CHEN Haitao, et al. Numerical simulation of vector wave scattering from the target and rough surface composite model with 3-D multilevel UV method[J]. IEEE Trans on Antennas Propag, 2010, 58(5): 1625-1634.
[9] KUANG Lei, JIN Yaqiu. Bistatic scattering from a three-dimensional object over a randomly rough surface using the FDTD algorithm[J]. IEEE Trans on Antennas Propag, 2007, 55(8): 1368-1376.
[10] EL-SHENAWEE M. The multiple interaction model for non-shallow scatterers buried beneath two dimen-sional random rough surfaces[J]. IEEE Trans on Geoscience and Remote Sensing, 2002, 40(4):982-987.
[11] CHEN Rushan, HU Yanqin, FAN Zhenghong, et al. An efficient surface integral equation solution to EM scattering by chiral objects above a lossy half space[J]. IEEE Trans on Antennas Propag, 2009, 57(11): 3586-3593.
[12] DECHAMPS N, DE BESUCOUDREY N, BOURLIER C, et al. Fast numerical method for electromagnetic scattering by rough layered interfaces: propagation-inside-layer-expansion method[J]. J Opti Soc Amer A, 2006, 23(2): 359-369.
[13] KUBICKE G, BOURLIER C, SAILLARD J. Scattering from canonical objects above a sea-like one-dimensional rough surface from a rigorous fast method[J]. Waves in Random and Complex Media, 2010, 20(1):156-178.
[14] TSANG L, KONG J A, DING K H. Scattering of Electromagnetic Waves: Numerical Simulations[M]. New York: John Wiley and Sons Inc, 2000: 278-285, 565-571.
[15] RAO S M, WLTON D R, GLISSON A W. Electromagnetic scattering by surfaces of arbitrary shape[J]. IEEE Trans on Antennas Propagat, 1982, 30(3): 409-418.
[16] TOPORKOV J V, BROWN G S. Numerieal simulations of scattering from time-varying, randomly rough surfaees[J]. IEEE Trans on Geosciences and Remote Sensing, 2000, 38(4): 1616-1625.

