场路结合法分析设备电磁辐照效应
郝建红 孙娜燕 高 璞 范杰清
(华北电力大学电气与电子工程学院,北京 102206)
引 言
目前,针对电磁辐照效应的研究有许多方法,全波分析和多种物理场模拟计算虽然能全面反映问题的物理机制,但在物理建模和数值计算时比较困难。部分元等效电路法(PEEC)是一种有效的电路建模方法,该方法将三维空间的电磁结构等效为多个部分电阻、部分电容、部分电感等集总元件所组成的网络,利用已有的电路仿真软件如模拟电路仿真器(SPICE)来分析其结构特性。用PEEC方法可以有效模拟电磁辐射干扰效应,但是由于形成的等效电路网络规模太大,计算效率较低,若不考虑集总元件的频变效应,随着频率的升高,计算误差会逐渐增大。国外近几年提出了多种场路结合的方法来研究相关问题[1-2],以解决分析精度与计算能力上的矛盾。
基于场路结合思想,在参照文献[3]的基础上,充分利用全波分析技术和电路分析技术分别在电磁敏感性(EMS)计算中的准确性和高效性优势,以电磁场混合势积分方程(MPIE)为出发点,通过离散边界积分方程获得了散射场的阻抗矩阵和等效电路,并以内置多层印制电路板(PCB)的箱屏蔽体为例,研究外部电磁辐照下设备和电路的电磁耦合效应。与文献[3]相比,将外部电磁辐照干扰通过全波分析等效为电压(流)源,利用电路仿真软件分析内部复杂电路,最大限度地发挥了全波技术的准确性和电路技术的高效性。其分析方法不仅可以运用于具有外接导线设备和孔缝耦合问题的分析,而且对瞬态电磁干扰和高频(几百兆或GHz以上)干扰的分析都有实用价值。
1.外部电磁干扰等效源模型
为满足散热、通信和动力需要,设备和电路的屏蔽箱体上通常都有孔洞和外接信号线或电源线,这破坏了箱体完整性,导致外部电磁干扰很容易通过屏蔽体上的这些孔洞和电缆线耦合进入屏蔽体内,干扰甚至损坏箱体内部的电路。
以一个带有电缆线、内置多层PCB的屏蔽箱体设备为例,通过电磁场混合势积分方程建立外部电磁干扰(EMI)对系统耦合的近似模型。
为方便分析EMI对设备的耦合效应,将整个问题分为内外两部分。外部问题包括屏蔽外壳、与机箱外壳相接的信号线或电源线;内部问题为印制板或各种电子线路。外部问题通过电磁场积分方程的全波分析按照电路理论抽象为一个等效源模型,其描述了外部电磁干扰经过各种通道耦合到内部电路中的电磁能量,等效源模型的参数可以利用矩量法计算电磁场混合势积分方程来获取;内部电路的分析往往比较复杂,可以利用导线与内部电路的电气连接特性,建立电路模型,来模拟外部电路对内部电路的影响。
1.1 外部电磁场混合势积分方程数值模型
假设设备外壳和电缆线都为理想导体,当外界电磁波入射到机壳和导线的表面上时会感应出电流J.根据边界条件,在导体表面S处
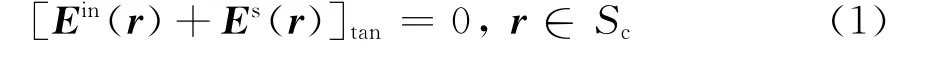
式中:Es(r)是由感应电流J产生的散射电场;Ein(r)是入射场。散射电场可以由矢势A和电势φ表示。
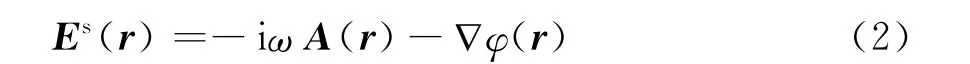
通过边界条件(1)知
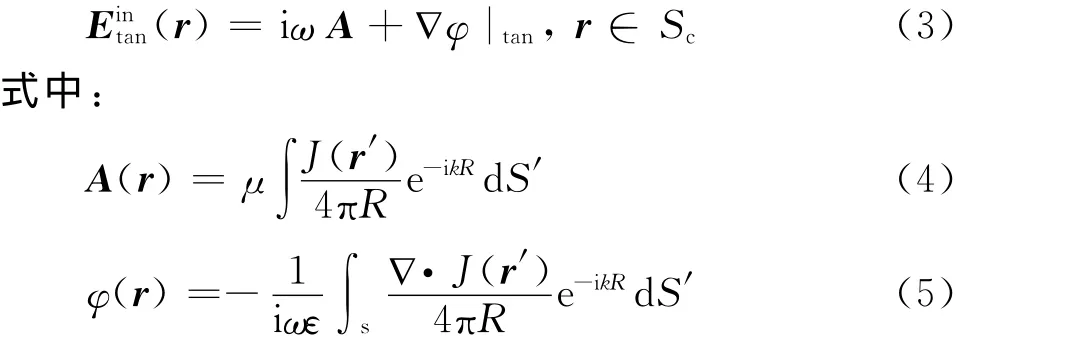
式中:ω和k分别是辐射电磁场的角频率和波数;R=|r-r′|表示源点到任意观察点的距离,r和r′分别为场点(x,y,z)和源点(x′,y′,z′)的位置矢量;μ,ε是空间的磁导率和电导率;i=表示虚数单位;tan表示正切。
针对线、面和线面连接的结构特点,分别选择三角函数、RWG函数和交叉函数作为基函数,将理想导体表面上的感应电流密度J(r)展为
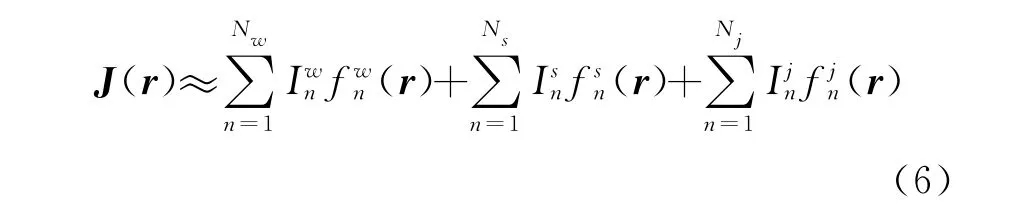
式中:分别是三角基函数、RWG基函数和交叉基函数的展开系数;Nw,Ns,Nj分别是三角基函数、RWG基函数和交叉基函数的个数。
采用伽辽金法,得到线性系统的矩阵方程
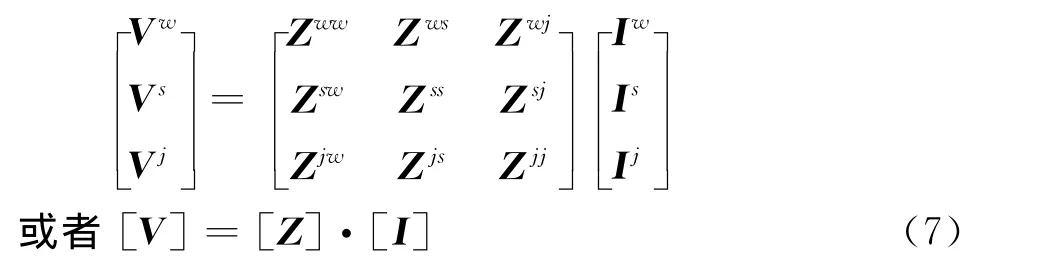
其中:Vp,Ip是长度为Np的列向量;[Zpq]是一个Np×Nq矩阵,且p,q=w,s,j.通过LU 分解,求解该矩阵方程就可得到线、面和线面连接处的电流展开系数,进而获得散射体的表面电流分布。
1.2 等效源模型
主要讨论外部环境中任意电磁辐射场的等效源模型的建立。外部电磁干扰对设备内部电路的主要耦合途径是感应电流经过与外壳连接的导线进入设备内部,进而对内部电路产生影响。
假设外部电缆与屏蔽壳的连接点是电连接,所处EMI环境任意。根据诺顿定理,把导体表面产生的感应电磁场等效为一个外部电流源或电压源和一个输入阻抗。该等效源在节点处作为外部干扰源的输入,等效源的输入阻抗可以通过矩量法求得。在箱体和外部线缆的电连接点处施加δ电压,该节点的输入阻抗可以作为等效源模型中的等效输入阻抗Zin,通过下面方程计算可得
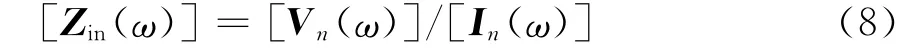
式中:[Vn(ω)]和[In(ω)]分别是节点的外加电压和感应电流矩阵,流过节点的感应电流可以通过1.1节的方法求解。该等效电流源模型需要经过两次计算,且两次计算的激励源不同,但是两次计算过程中阻抗矩阵 [Zin(ω)]是不变的,也就是说,阻抗矩阵[Zin(ω)]相同,电压向量不同。通过上述过程求出外部EMI的等效源参数,建立等效源模型如图1所示。
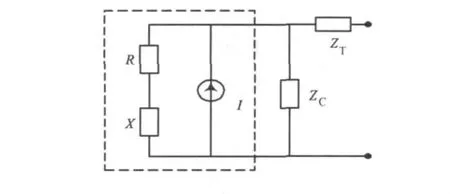
图1 外部电磁干扰的等效电流源模型
式中:R,X和I分别代表等效源电流内部的内阻、电抗和感应电流。使用电路原理求解时,X需要通过下面的公式转化为集总电容或电感,或两者的结合。
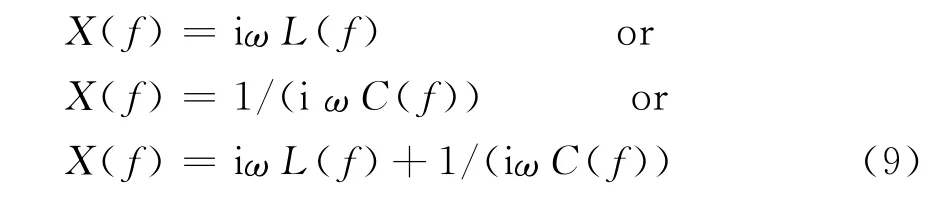
式中:L和C分别代表随频率变化的电感和电容,其它集总元件的参数需根据外部线缆进入箱体的方式和与电路的连接方式来决定:Zc代表箱体对地的漏电抗,其大小取决于线缆与机壳的连接方式,当Zc=∞时,表示线缆进入机壳的方式不是电连接的;ZT由线缆与内部电路的连接方式决定。
2.电磁辐射干扰等效源模型仿真
2.1 外部电磁干扰等效源模型的参数计算
利用1.2节建立的等效源模型针对一个具体的例子进行仿真分析。假设机箱和线缆均为理想导体,箱体尺寸为400mm×200mm×400mm,信号线长为500mm、半径1mm,设外部电磁干扰为一平面电磁波,其电场极化方向与信号线垂直,如图2所示,其中=1 V/m.
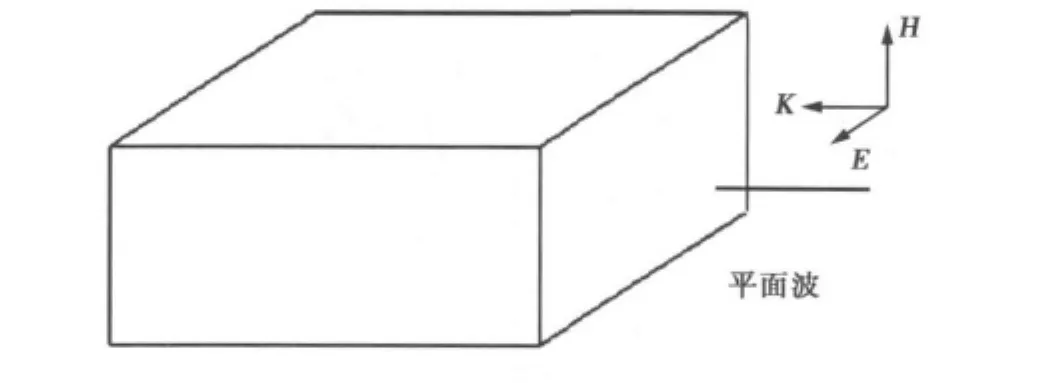
图2 平面波辐照下外接导线的屏蔽箱体
为了建立等效源集总元件模型,等效电流源的阻抗需要转化为随频率变化的电阻、电容或者电感的组合。求输入阻抗时,激励源要先换成δ电压,得出输入阻抗的实部和虚部(单位为kΩ)分别随频率变化的曲线,并与仿真结果相比较,两者拟合良好,如图3和图4所示。
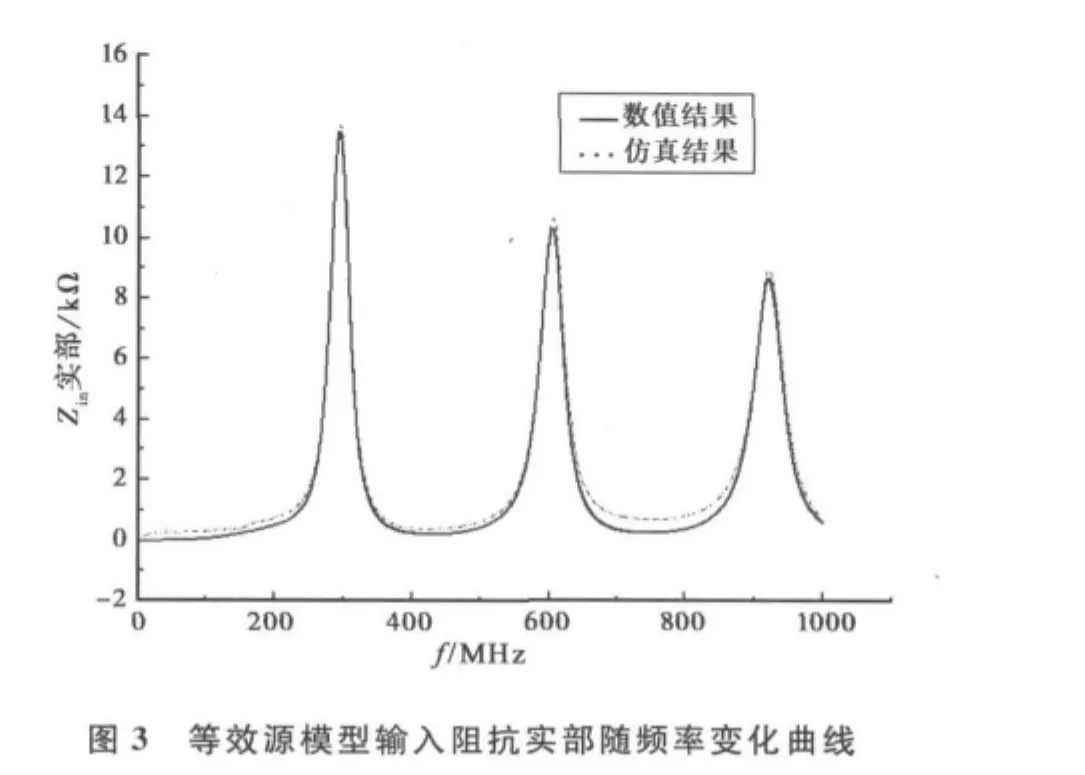
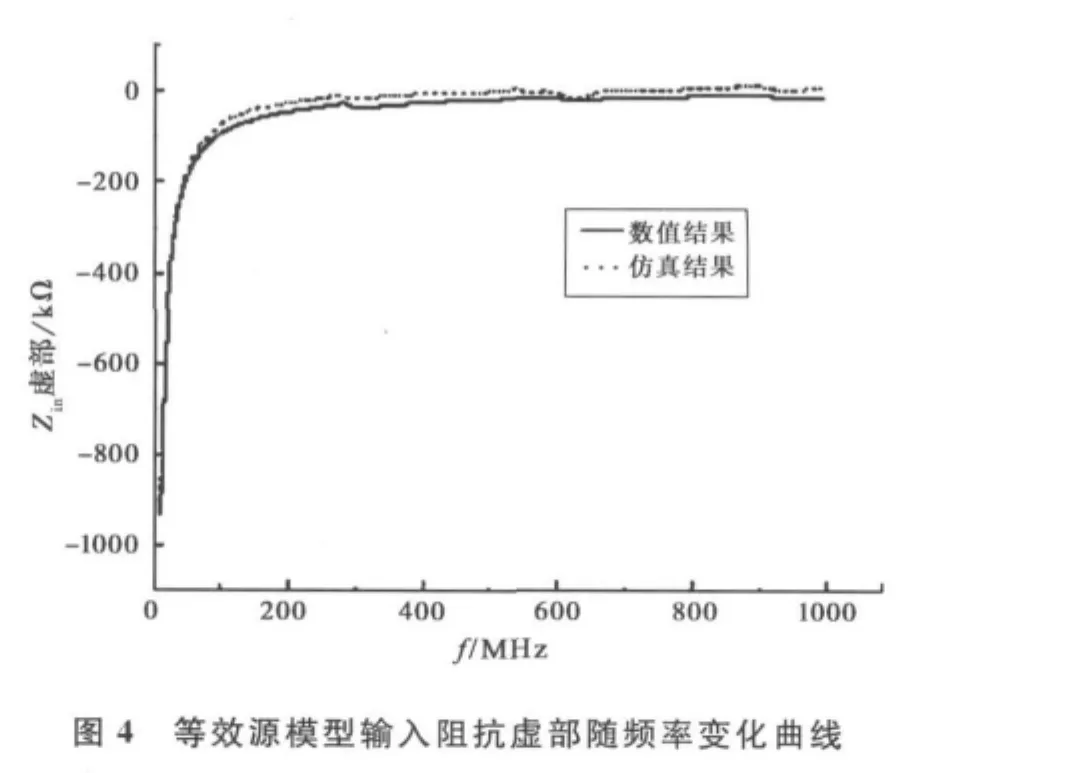
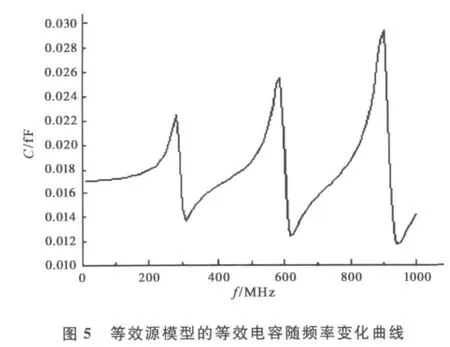
由图可知,复阻抗的实部为电路的电阻,虚部为电抗。由于电抗小于零,整个电路阻抗呈容性,这样等效源的输入阻抗可以转化为一个电阻和一个电容的组合。图5是等效电容(单位为fF)的幅值随频率变化的曲线,可以看出其幅值大小随频率呈波动性的变化,且频率越高,波峰的峰值就越大。
图6、图7分别给出感应电流幅值和相位随频率变化的曲线,其结果与仿真结果吻合良好。
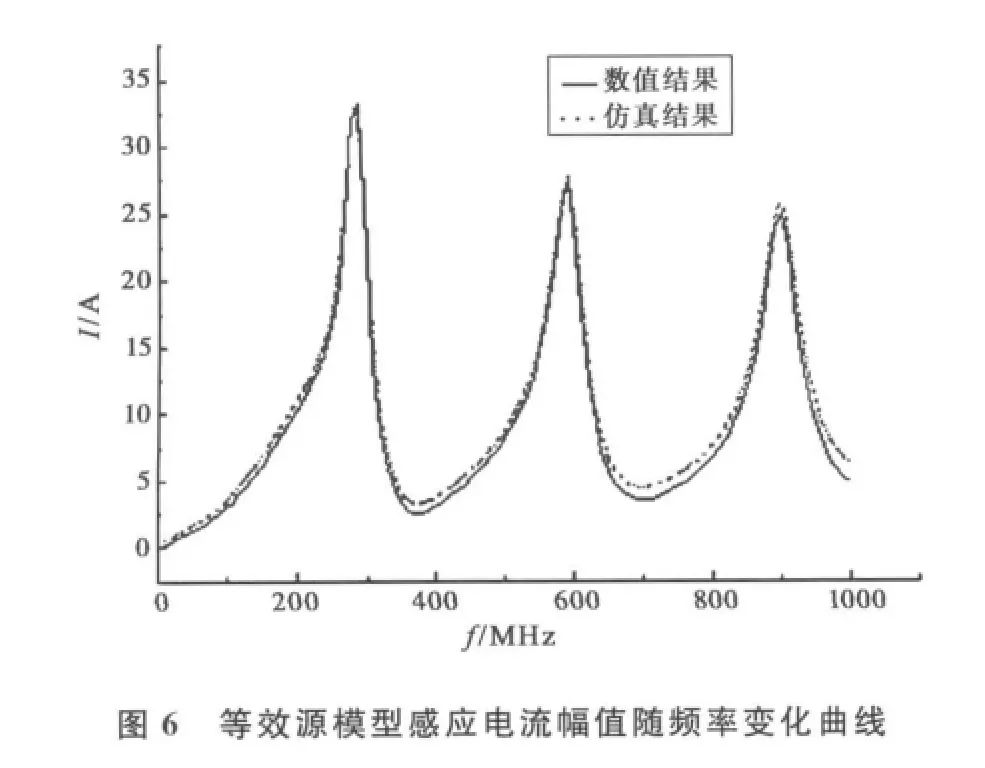
上述等效源方法可以推广到多条线缆的情况,也可以通过傅里叶变换对任意脉冲的EMI耦合效应进行时域和频域的分析。基于场路结合理论的等效源方法不仅克服了PEEC方法在高频情况下计算误差大的缺点,还大大节省了计算时间和计算机资源,其计算结果与纯计算技术软件仿真得到的结果吻合较好。
以一个内置PCB且外接电缆线的箱体为例,在外部电磁干扰等效源模型的基础上,与基于矩量法的电磁仿真分析软件相结合,对箱体内的PCB电磁特性进行分析计算。
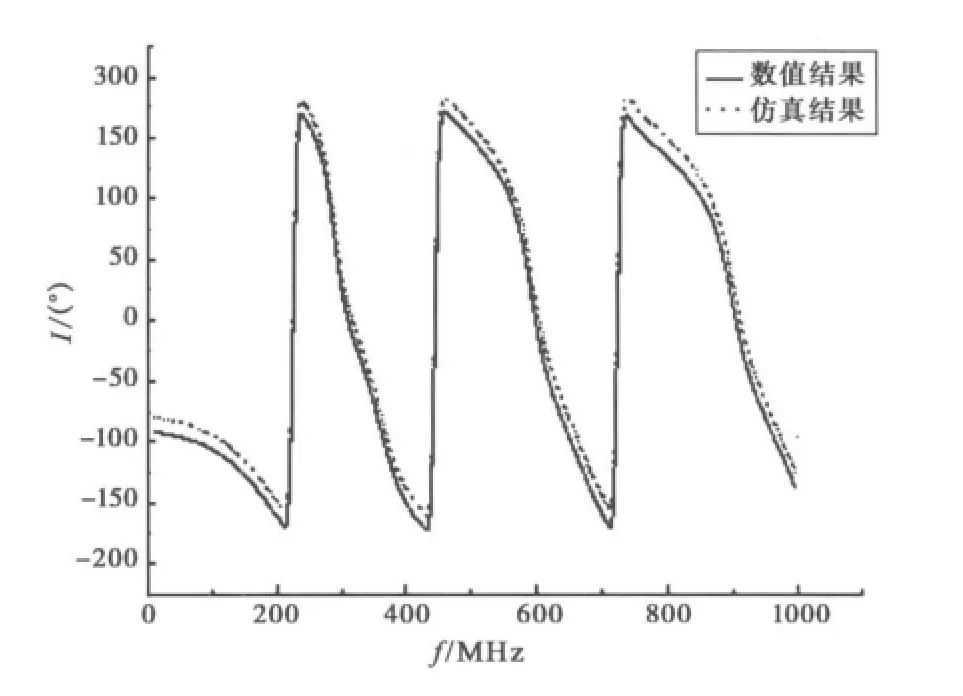
图7 等效源模型感应电流相位随频率变化曲线
2.2 内置多层PCB板设备的电磁耦合效应的计算和仿真
使用基于矩量法的电磁仿真分析软件搭建多层PCB电路模型,将外部电磁干扰等效源接入电路,观察负载输出的干扰电压变化情况以分析内部电路受到的干扰[4-6]。
图8是一个放置在模型1中的具有5条传输线的双层PCB板,其中PCB板厚0.2mm,传输线长200mm,宽0.4mm,厚0.06mm,传输线间距0.2 mm,介电常数εr=4.3.等效电流源模型包含一个交流电流源和一个二端口元件,且该元件的一端与PCB板上的节点4所在的传输线相连。若以连接点为分界,五条传输线在始末两端均连有10kΩ的电阻,这五条传输线间距相等为5mm,现选择9个节点为观察点(从上到下从左到右依次是节点8,2,7,3,4,9,5,10,6)来计算分析外部干扰对内部电路的影响。
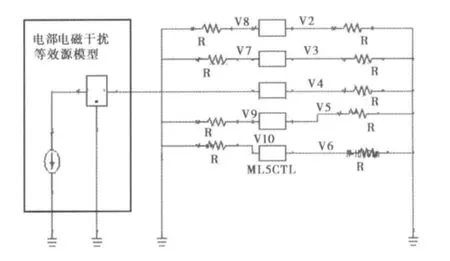
图8 包含5条传输线的双层PCB板
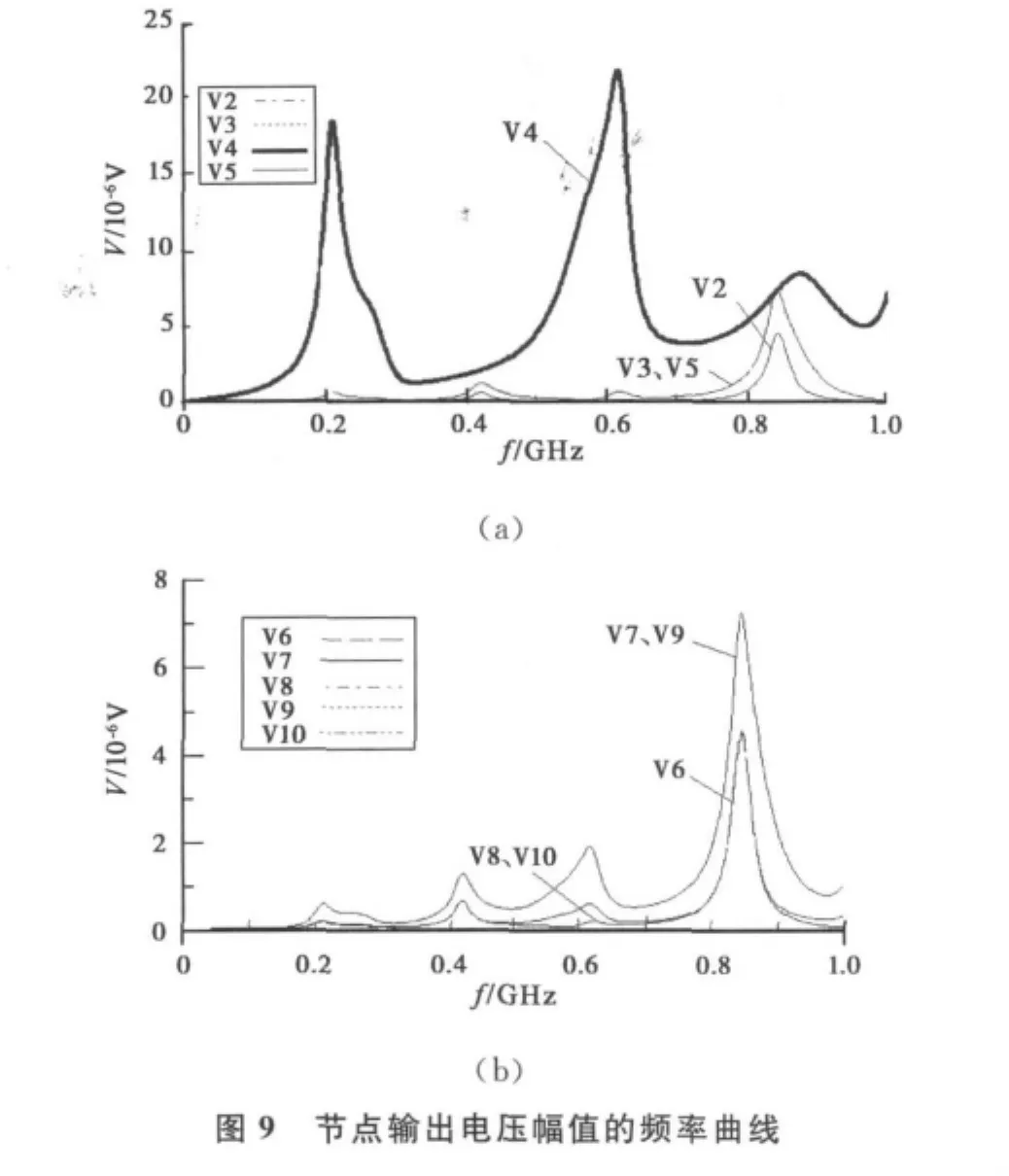
图8中9个节点输出电压的变化情况,如图9(a)和9(b)所示。图(a)分别是 V2、V3、V4和 V5随频率变化的曲线,图(b)是V6-V10随频率变化的曲线。除节点4以外,其它节点输出电压的峰值频率几乎都在830MHz附近,而且节点离参考地越近,输出电压在低频范围(小于0.7GHz)内幅值越小、也越接近于零,说明对抑制低频干扰能力越强。
如果负载大小发生改变,就可观察负载对节点电压的影响。将节点6作为一个观察点,其对地的负载分别取500Ω,1kΩ,3kΩ,5kΩ,10kΩ,那么可以得到这几个负载情况下输出电压随频率变化的曲线,如图10所示。
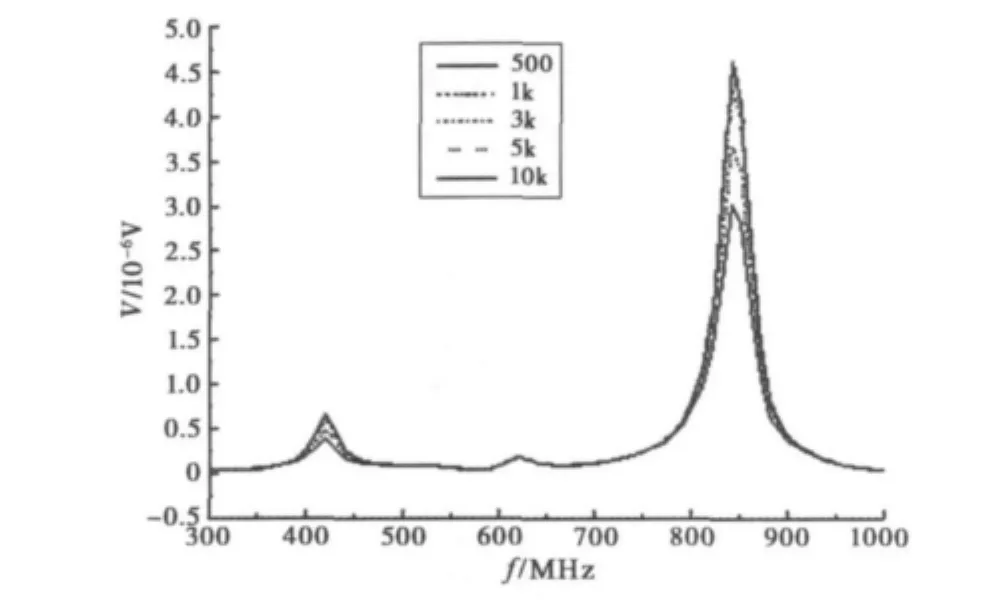
图10 节点6输出电压幅值随负载变化的频率曲线
由图10可知:V6出现峰值的频率点基本与负载无关,这是由于峰值点的频率往往与箱体的尺寸、导线的长度和半径有关[7-9]。输出电压峰值随负载的增大而增大,但负载增大到一定的值就相当于开路,即使负载继续增大,峰值也几乎不变。在高频(大于0.7GHz)范围内,干扰电压的峰值远远大于低频范围的峰值,表明环境中的高频电磁干扰对电子设备有更大的影响。
3.结 论
目前电磁环境日益复杂,高频(几百MHz到几十GHz)电磁干扰容易由导线感应耦合进入设备内部产生干扰,甚至可能让设备丧失工作能力。电磁辐照效应的研究最严格的方法当属全波分析和多物理场模拟计算,但以目前的建模水平和计算能力,完全电磁场分析计算还难以实现。以电磁场混合势积分方程作为出发点,采用全波分析与等效电路相结合的方法,通过计算外部电磁干扰的等效源参数,建立其等效源模型,并对具体电路实例进行了计算和分析。与单纯的电磁场计算技术相比,本方法具有计算过程简单、计算精度和计算效率高等优点。
[1]KODALI V P.Engineering Electromagnetic Compatibility[M].New York:Institute of Electrical and Electronics Engineers Inc,2004.
[2]SCHUSTER C,FICHTER W.Parasitic modes on printed circuit boards and their effects on EMC and signal integrity[J].IEEE Trans Electromagnet Compat,2001,43(4):416-425.
[3]LIANG Y W,L I E P.A systematic coupled approach for electromagnetic susceptibility analysis of a shielded device with multilayer circuitry[J].IEEE Transaction on Electromagnetic Compatibility,2005,47(4):692-699.
[4]PHYU H N,LI E P,LIANG Y W.Analysis of Electromagnetic Susceptibility on High Speed Circuits Located in a Shielded Enclosure[C]// Proceedings of 17th International Zurich Symposium on Electromagnetic Compatibility.Piscataway,USA,2006:312-315.
[5]付继伟,候朝桢,窦丽华.电磁脉冲斜入射时对孔缝耦合效应的数值分析[J].强激光与粒子束,2003,15(3):249-252.FU Jiwei,HOU Chaozheng,DOU Lihua.Numerical analysis on hole coupling effects of an obliquein cidence of electromagnetic pulse[J].High Power Laser and Particle Beams,2003,15(3):249-252.(in Chinese)
[6]姜雪松,王 鹰.电磁兼容与PCB设计[M].北京:机械工业出版社,2008:102-110.
[7]陈修桥,胡以华,张建华.计算机机箱的电磁脉冲耦合模拟仿真[J].系统仿真学报,2004,12:2786-2788.CHEN Xiuqiao,HU Yihua,ZHANG Jianhua.The coupled simulation of electromagnetic plus in computer chassis[J].Journal of System Simulation,2004,12:2786-2788.(in Chinese)
[8]范颖鹏,杜正伟,龚 克.不同形状孔阵屏蔽效应的分析[J].强激光与粒子束,2004,16(11):1441-1444.FAN Yingpeng,DU Zhengwei,GONG Ke.Shielding effect of different shapes hole array analysis[J].High Power Laser and Particle Beams,2004,16(11):1441-1444.(in Chinese)
[9]邹国平,崔 翔,魏兴昌,等.高速电路电源/地层间阻抗参数计算与分析[J].电波科学学报,2010,26(2):394-399.ZOU Guoping,CUI Xiang,WEI Xingchang,et al.Calculation and analysis of the impedance parameters of high-speed circuit's power-ground planes[J].Chinese Journal of Radio Science,2010,26(2):394-399.(in Chinese)

