基于简缩极化数据的三分量分解模型

刘 萌 张 红 王 超

（1.中国科学院对地观测与数字地球科学中心数字地球中科院重点实验室，北京 100094；2.中国科学院研究生院，北京 100086）

引 言

极化雷达这一概念在1950年被首次提出，自此以后，特别是最近的20年里，合成孔径雷达（SAR）极化测量技术有了很大的提高，其应用领域也越来越广泛［1-3］。全极化干涉合成孔径雷达（F-PolIn-SAR）的出现为雷达技术的应用开创了更有前景的应用，尤其在树高估计、多层地形信息提取等森林遥感方面［4］。随着雷达数据质量的不断提高，全极化（FP）干涉雷达的阶段已经来临。但是，现在星载全极化干涉系统还存在着数据下载速度、测绘带宽、能量消耗、天线技术等限制因素。为了克服这些因素的限制，一个新的雷达极化技术——简缩极化（CP）测量被提出［5］。在CP系统中，雷达发射圆极化波或极化方位角为45°的线极化波，用水平、垂直线极化的方式或者左、右圆极化的方式接收回波［6-8］。与全极化合成孔径雷达系统相比，简缩极化合成孔径雷达系统较全面保持了极化SAR信息，有效降低了对SAR系统复杂度及数据下传速率的要求。

近些年，随着人们对CP系统的研究逐渐增多，简缩极化成为极化领域的一个研究热点［9-10］。2005年，Souyris等人在极化相干度和交叉极化率之间的关系以及反射对称的假设下，提出了一种由CP数据重建FP数据的方法，Nord等人于2009年对该方法进行了进一步改进［6］。2007年，Raney基于CP数据的Stokes矢量提出了CP数据的m-δ分解方法［11-12］，这种方法不需要进行伪FP信息的重建，基于Stokes参数，可以得到极化度、回波相位差等有利于理解目标散射机理的参数。在m-δ分解方法的基础上，Charbonneau等人研究了CP数据在农业、冰川以及变化检测方面与全极化数据的对比应用［13］。2009年，L.Chen等人基于CP数据，提出了一种利用极化功率和Wishart分类器对CP图像进行地物非监督分类的方法［14］。在简缩极化干涉方面，Angelliaume等人［15］和谈璐璐等人［16］开展了CP数据在极化相干最优、树高提取的研究。

目前，在对CP数据进行极化和极化干涉测量的处理时，除了m-δ分解外，都需要首先利用CP重建伪FP协方差矩阵，然后再利用全极化处理方法反演相应参数。但是，重建FP信息需要反射对称及极化相干度、交叉极化率之间的关系等假设，这些条件会给测量结果带来较大误差［17］。以反射对称假设为例，并不是所有散射地物都是关于雷达照射平面对称的，特别是对于极不均匀区域，反射对称的假设很难成立。鉴于以上原因，文章首次尝试在不重建伪FP协方差矩阵的情况下，开展基于CP数据的三分量分解模型的研究。该模型将简缩极化数据的Jones相干矩阵分解成表面散射、偶次散射和体散射三种散射机制的Jones相干矩阵之和，进而建立方程得到三种散射机制各自的散射功率。由于该模型不需要进行伪FP信息的重建，因此，可以消除极化相干度和交叉极化率之间的关系这一假设条件带来的不必要测量误差。另外，模型没有关于地物反射对称的假设，这更符合目标物理散射体现，有效提高分解精度。

1.简缩极化数据的STOKES参数

对于CP系统，给出它的入射波和散射波的Jones矢量:Ei+和Es-，那么目标的散射过程可以表述为

式中:上标i+和上标s-表示电磁波传播的不同方向；矢量S称为CP系统的散射矢量。由于CP系统中雷达只发射一种特定的波形，所以CP系统中入射波的Jones矢量退化为一个复数。Ei+和Es-表示在相同极化态下波传播方向的不同，通过计算时间反演［18］，可以得到入射波方向上散射波的Jones矢量E为

式中:上标＊表示复共轭运算。根据散射波的Jones矢量E，可以得到CP系统散射电场的2×2复艾米特半正定相干阵，也叫做Jones相干矩阵J，其表达式为

式中:〈…〉表示空间平均；上标T表示矩阵转置。从式（3）可以看到:当入射波Ei+的能量为1时，CP数据的Jones相干矩阵可以直接由其散射矢量S得到。根据Stokes矢量与Jones相干矩阵的转换关系，可以得出CP数据的Stokes矢量表达式为

式中:δ表示散射波E的两个正交分量Es+cp1和Es+cp2之间的相位差，参数｛g0，g1，g2，g3｝是 Stokes参数。根据Stokes参数，可以求得极化度m和散射波H-V相对相位差δ，表达式如下

式中:ℜ表示复数的实部；ℑ表示复数的虚部；m和δ是Raney分解的两个分解参数，m是部分极化波的重要指标，δ对后向散射场的极化变化十分敏感，它可以反映出地物的散射类型。

2.部分极化波的二分理论

根据部分极化波二分理论，任何一个部分极化波都可以分解成一个完全极化波和一个完全非极化波之和，分解后的两个波时完全不相干且唯一［19］。因此，任一部分极化波的Jones相干矩阵J都可以表示为

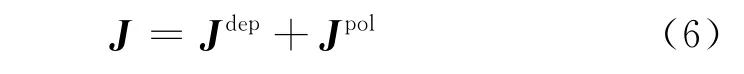
式中:Jdep为分解后完全非极化波的Jones相干矩阵；Jpol为分解后完全极化波的Jones相干矩阵。这两个矩阵可以表示为

4.简缩极化的三分量分解模型

如前所述，简缩极化SAR系统发射具有特定极化状态的单一极化波，用两路相互正交的极化方式接收信号［16］。根据发射及接收电磁波的极化状态，提出了若干不同的简缩极化模式，常用的有3种模式:圆周极化发射线性极化接收（CTLR）模式，双圆周极化（DCP）模式和π／4模式［4，20］。CTLR模式下，雷达发射左旋或右旋圆极化波，用水平极化和垂直极化方式接收回波；DCP模式下，雷达发射左旋或右旋圆极化波，用左旋圆极化和右旋圆极化方式接收回波；π／4模式下，雷达发射45°线极化波，用水平极化和垂直极化方式接收回波。对于不同的模式，在相同散射机制下对应的散射矢量S是不同的。以CTLR模式为例，也称为混合极化模式［11-12］，说明提出的三分量分解模型。假设雷达发射的是右旋圆极化波，该模式对应的散射矢量S为

根据散射矢量S，结合第1部分的公式（3），就可以得到CTLR模式的Jones相干矩阵J，表达式见式（10）.

对于简缩极化，三分量分解是将散射目标的Jones相干矩阵表示成各个基本散射机制Jones相干矩阵之和的形式。常见散射机制有:奇次散射、偶次散射和体散射等，下面推导这三种散射机制在CP情况下的Jones相干矩阵。

体散射成份代表散射目标中最复杂的散射部分，在单站全极化系统中，体散射对应的相干矩阵3个特征值几乎相等，极化散射熵接近1.目前，体散射的全极化散射矩阵和相干矩阵都没有统一表述，不同的假设模型会得到不同的矩阵表达式。此处认为体散射是一个完全随机的散射过程［21］，即对应于极化熵为1的散射过程。

在简缩极化情况下，体散射对应于目标Jones相干矩阵中的完全非极化部分，因此，其Jones相干矩阵即是完全非极化波的Jones相干矩阵，表达式Jv为

在全极化中，表面散射对应的散射矩阵S为

RH和RV表示水平极化和垂直极化的反射系数。联立式（9），式（10）和式（12），可以得到 CTLR 模式下，表面散射对应的Jones相干矩阵Js为

在全极化中，偶次散射对应的散射矩阵S为

式中:Rth和Rtv分别表示偶次散射中垂直表面上水平极化和垂直极化的反射系数；Rgh和Rgv分别表示偶次散射中水平表面上水平极化和垂直极化的反射系数；γh和γv分别表示水平极化波和垂直极化波的衰减和相位变化。联立式（9），式（10）和式（15），可以得到CTLR模式下偶次散射对应的Jones相干矩阵，其表达式Jd为

目标的Jones相干矩阵J可以看成是体散射、表面散射和偶次散射三个散射类型的Jones相干矩阵之和。因此，可以得到

式中:Pv、Ps和Pd分别表示体散射、表面散射和偶次散射对目标的Jones相干矩阵J的贡献；J′表达式见式（19）。

比较式（18）和式（6），可以发现式（18）的第一项PvJv对应式（6）中的第一项，即目标Jones相干矩阵J中的完全非极化部分；式（18）的后两项之和J′对应式（6）中的第二项Jpol，即目标Jones相干矩阵J中的完全极化部分。结合式（7），（8）和（19），可以得到

式（20）给出了4个方程，其中A，B，C，D 可以由式（8）求得，方程中共有Pv，Ps，Pv，α，β等5个未知数。从式（20）中的第一个方程Pv=2A可知，体散射分量功率Pv可以直接由Jdep得到，就得到一个拥有4个未知数、3个方程的不定方程组。一般情况下，这样的方程组有无穷多组解。可以通过判断偶次散射和表面散射哪个在Jpol中占主要贡献的方法来求解Ps和Pd.由于假设雷达入射波为右旋圆极化波，它的Stokes矢量表达式为

对应的入射波H-V相对相位差δ为-90°，Raney在右旋混合极化SAR数据的m-δ分解中指出:当散射波H-V相对相位差δ接近-90°时，对应地物的散射类型为偶次散射；当散射波H-V相对相位差δ接近90°时，对应地物的散射类型为表面散射［11-12］。另外，由地物散射机理可知，当地物的散射类型以表面散射为主时，将会在与入射波相反的极化态方向上产生很强的后向散射，使得散射波的H-V相对相位差δ变为正值；当地物的散射类型以偶次散射为主时，将会在与入射波相同的极化态方向上产生很强的后向散射，使得散射波的H-V相对相位差δ仍为负值［14］。因此，可以用散射波H-V相位差δ来反映出散射目标的主要散射类型，如果δ是正值，说明该散射目标中表面散射占主导作用，令α=-1；如果δ是负数，说明该散射目标中偶次散射占主导作用，令β=1.通过以上判断，将附件条件带入方程组便可以估计出Ps和Pd.

4.实验及讨论

选取德国代根多夫市普拉特灵（Plattling）地区的TerraSAR-X全极化数据作为实验数据，该图像的获取时间是2009年7月10日。首先根据式（9）将全极化数据模拟生成CTLR模式下的CP数据，然后得到CP数据的Jones相干矩阵，使用提出的三分量分解模型对Jones相干矩阵进行分解。将分解结果进行彩色合成 （Ps:蓝色，Pd:红色，Pv:绿色），如图1（a）所示。为了检验该模型的分解效果，将该模型的分解结果与使用相同RGB合成方式的全极化Pauli分解结果进行对比，如图1（b）所示。

注意到图1（a）和图1（b）有一些不同，尤其在城区部分。图2（a）和图2（b）为图1（a）和图1（b）中城区部分的对比图，城区以偶次散射为主，在分解结果中的RGB合成图中应主要显示为红色。而图2（a）中显示城区以黄色为主，因为黄色是红色和绿色的合成色，这说明简缩极化分解结果中偶次散射成分比全极化分解中的偶次散射成分稍低，也说明提出的模型高估了体散射成分。

表1给出了在CP数据三分量分解和FP数据Pauli分解中，表面散射占主导、偶次散射占主导和体散射占主导的像素个数的统计信息。从表1可以看出:两种分解中表面散射占主导的像素个数相当，占到总像素的7%左右。但CP数据三分量分解中偶次散射占主导的像素个数比FP数据Pauli分解要少，这也说明CP数据的三分量分解会使偶次散射成分低估。

表1 三种散射机制在CP和FP分解中像素个数统计

造成这种结果的原因有2个，首先，当散射波的H-V相对相位差δ接近0时，它已不能准确地反映出地物的散射类型，这时使用δ来判断偶次散射或是表面散射在J占主导作用的方法效果并不理想。另外，由式（19）可得

说明矩阵J′的行列式是非负的，而完全极化波的Jones相干矩阵应该是0，根据极化波的二分理论可知，矩阵J′仍可分成一个完全极化波和一个完全非极化波之和，即J′中仍然包含完全非极化成分。因此，模型中将矩阵J′直接对应目标Jones相干矩阵中的完全极化部分是不准确的，将导致体散射的高估，这就解释了图像中的偶次散射在图2（b）显示为红色，而在图2（a）显示为黄色的原因。但总的来说，两种分解方法在表面散射和体散射上有很强的相似。

5.结 论

基于部分极化波的二分理论，针对目标的Jones相干矩阵，提出了一种简缩极化数据的三分量分解模型，将目标的Jones相干矩阵分解成体散射、表面散射和偶次散射三种散射类型的Jones相干矩阵之和。研究的主要结论如下:

1）能够不进行伪FP信息的重建，直接根据部分极化波的二分理论，对简缩数据的Jones相干矩阵进行极化分解。这样可以消除重建伪FP数据时反射对称及极化相干度、交叉极化率之间的关系等假设条件带来的不必要误差，提高分解精度。

2）通过比较提出模型的分解结果和全极化数据的分解结果，发现提出的分解模型能够很好地描述表面散射和体散射的散射行为。

3）提出的简缩极化的三分量分解高估了目标的体散射成分，造成分解结果中偶次散射的成分偏低，这个问题需要进一步地研究来解决。

［1］张 波，王 超，张 红，等.Radarsat-2全极化SAR车辆目标典型方位特性分析［J］.电波科学学报，2010，25（6）:1135-1139+1233.ZHANG Bo，WANG Chao，ZHANG Hong，et al.Radarsat-2quad-pol SAR image signature analysis of road trucks［J］.Chinese Journal of Radio Science，2010，25（6）:1135-1139+1233.（in Chinese）

［2］吴 樊，陈 曦，王 超，等.基于极化似然比的极化SAR影像变化检测［J］.电波科学学报，2009，24（1）:120-125.WU Fan，CHEN Xi，WANG Chao，et al.Change detection based on polarimetric test statistic for multi-polarization SAR imagery［J］.Chinese Journal of Radio Science，2009，24（1）:120-125.（in Chinese）

［3］范立生，高明星，杨 健，等.极化SAR遥感中森林特征的提取［J］.电波科学学报，2005，20（5）:553-556.FAN Lisheng，GAO Minxing，YANG Jian，et al.Feature extraction of a forested area based on polarimetric SAR［J］.Chinese Journal of Radio Science，2005，20（5）:553-556.（in Chinese）

［4］李廷伟，梁甸农，黄海风，等.植被分布式SAR极化干涉复相关系数建模与分析［J］.电波科学学报，2010，25（3）:415-423.LI Tingwei，LIANG Diannong，HUANG Hai feng，et al.Modeling and analyzing complex coherence for vegetation observed by distributed polarimetric SAR interferometric system［J］.Chinese Journal of Radio Science，2010，25（3）:415-423.（in Chinese）

［5］SOUYRIS J C，IMBO P，FJORTOFT R，et al.Compact polarimetry based on symmetry properties of geophysical media:The pi／4mode［J］.IEEE Transactions on Geoscience and Remote Sensing，2005，43（3）:634-646.

［6］NORD M E，AINSWORTH T L，LEE J S，et al.Comparison of compact polarimetric synthetic aperture radar modes［J］.IEEE Transactions on Geoscience and Remote Sensing，2009，47（1）:174-188.

［7］LAVALLE M，POTTIER E，SOLIMINI D，et al.Compact polarimetric SAR interferometry:PALSAR observations and associated reconstruction algorithms［C］／／the 4th International Workshop on Science and Applications of SAR Polarimetry and Polarimetric Interferometry.Frascati，Italy，2009.

［8］TRUONG-LOI M L，DUBOIS-FERNANDEZ P，POTTIER E，et al.Polarimetric analysis from compact-pol measurements:potential and limitation［C］／／IGARSS.Cape Town，2009:V-1-V-4.

［9］CLOUDE S R.Dual versus quadpol:a new test statistic for radar polarimetry［C］／／PolInSAR 2009.Frascati，Italy，2009.

［10］TOUZI R.Compact-hybrid versus linear-dual and fully polarimetric SAR［C］／／PolInSAR 2009.Frascati，Italy，2009.

［11］RANEY R K.Decomposition of hybrid-polarity SAR data［C］／／PolInSAR 2007.Frascati，Italy，2007.

［12］RANEY R K.Hybrid-polarity SAR architecture［J］.IEEE Transactions on Geoscience and Remote Sensing，2007，45（11）:3397-3404.

［13］CHARBONNEAU F，BRISCO B，MCNAIRN H.Compact polarimetry:multi-thematic evaluation［C］／／PolInSAR 2009.Frascati，Italy，2009.

［14］CHEN L，CAO F，HONG W.Unsupervised classification for compact polarimetric SAR data using m-delta decomposition，SPAN and the Wishart classifier［C］／／2nd Asian-Pacific Conference on in Synthetic Aperture Radar，2009:742-745.

［15］ANGELLIAUME S， DUBOIS-FERNANDEZ， P SOUYRIS J C.Compact PolInSAR for vegetation char-acterisation［C］／／Geoscience and Remote Sensing Symposium.Barcelona，2007:1136-1138.

［16］谈璐璐，杨立波，杨汝良.合成孔径雷达简缩极化干涉数据的植被高度反演技术研究［J］.电子与信息学报，2010，32（12）:2814-2819.TAN Lulu，YANG Libo，YANG Ruliang.Investigation on vegetation height retrieval technique with compact PolInSAR data［J］.Journal of Electronics ＆Information Technology，2010，32（12）:2814-2819.（in Chinese）

［17］REIGBER A，NEUMANN M，et al.MULTI-Baseline coherence optimisation in partial and compact polarimetric modes［C］／／Geoscience and Remote Sensing Symposium，IGARSS.Boston，MA，2008:II-597-II-600.

［18］LUNEBURG E，CLOUDE S R.Radar versus optical polarimetry［C］／／Wideband Interferometric Sensing and Imaging Polarimetry.San Diego，CA，USA，1997:361-372.

［19］BORN M，WOLF E.Principles of Optics［M］.7th ed.New York:Pergamon，2003.

［20］AINSWORTH T L，PREISS M，STACY N，et al..A-nalysis of compact polarimetric SAR imaging modes［C］／／PolInSAR.Frascati，Italy，2007.

［21］AN Wentao，CUI Yi，YANG Jian.Three-component model-based decomposition for polarimetric SAR data［J］.IEEE Transactions on Geoscience and Remote Sensing，2010，48（6）:2732-2739.