加载与约束结合的主瓣干扰抑制方向图保形

刘聪锋 杨 洁 甘 昶

（1.西安电子科技大学电子对抗研究所，陕西 西安 710071；2.西安邮电学院通信与信息工程学院，陕西 西安 710121）

引 言

自适应阵列的应用可以有效抑制空间存在的干扰信号，尤其当干扰信号位于主瓣外时，阵列天线可以利用自适应波束形成实现干扰的有效抑制，然而当干扰位于主瓣内时，应用常规自适应波束形成技术将导致副瓣电平增高、主波束变形且峰值偏移，从而输出信号与干扰和噪声的功率之比（SINR）下降，虚警概率急剧上升，同时峰值偏移也将影响测角的精度［1-4］。究其原因，是由于自适应波束形成为抑制主瓣干扰，必须在主瓣内形成零陷所致。

提出了多种方法用于抑制主瓣干扰［3-8］，但是在消除主瓣干扰的同时也引起了其它问题，如主瓣指向偏移、旁瓣升高等。基于阻塞矩阵预处理的主瓣干扰抑制方法由于其思路清楚、效果显著得到了广泛的关注［4］，但是该方法也会有主波束指向偏移等问题。为此，提出了在数据阻塞矩阵预处理之后，利用对角加载与线性约束相结合的方法来改善预处理后的自适应波束形成性能，即校正由预处理引起的主瓣指向偏移，利用线性约束改善对其它干扰的抑制性能。其中不仅对数据阻塞矩阵预处理后的波束形成算法指向偏移原因进行了深入分析，给出了相应的解决方法，所提方法应用简单而有效。

1.基于阻塞矩阵预处理的主瓣干扰抑制

文献［4］提的主瓣干扰抑制方法实现如下。

假设主瓣内存在一个干扰，可以首先利用空间谱估计方法对主瓣干扰进行方位估计。由于干扰强度远远大于目标信号及噪声的强度，因此，空间谱估计选用较为简单的最小方差或多重信号分类（MUSIC）算法即可。其中基于MUSIC算法估计主瓣干扰方位的公式为

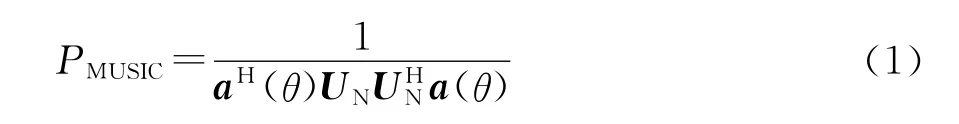
式中:UN为阵列接收信号的协方差矩阵R经特征分解后得到的噪声子空间特征矢量矩阵；a（θ）为导向矢量。MUSIC谱峰所对应的角度值就是所要估计的信号和干扰的入射方向。由于只对主瓣干扰进行定位，故上式的角度搜索范围只需在主波束内进行，从而大大减少了运算量。

得到主瓣干扰的方位信息后，对阵列接收信号X进行主瓣干扰相消预处理。设处理后的信号为Y，则有

其中B为（N-1）×N维的预处理阻塞矩阵，N为阵元数，且

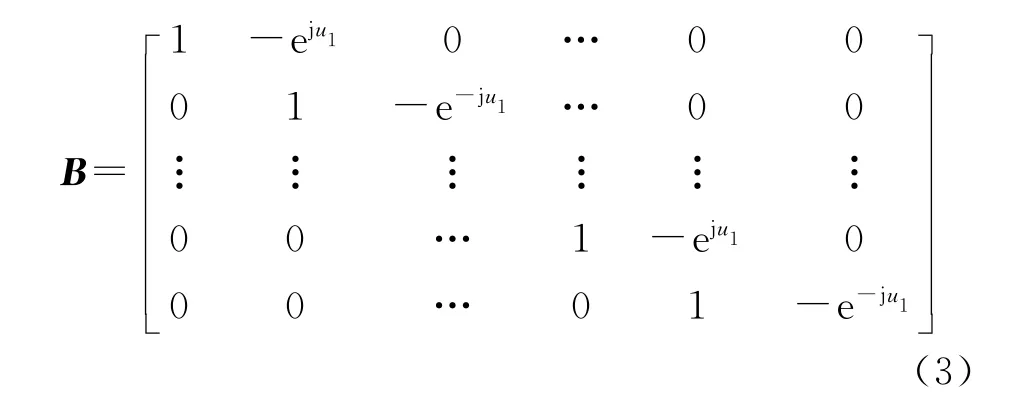
式中:u1=2π（d／λ1）sinθ1；θ1为主瓣干扰的方位角；λ1为干扰信号的波长；d为阵元间距。B实质上是一个信号阻塞矩阵，它利用相邻天线单元进行相消处理来抑制主瓣干扰。显然，Y为N-1维向量。如果假设接收阵列是阵元间距为d的均匀线阵，则在预处理变换前，第k个天线单元的接收信号可表示为

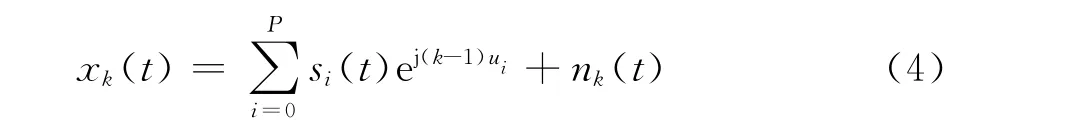
式中:k=1，2，…，N；ui=2π（d／λi）sinθi表示第i个信号或干扰到达阵列天线相邻阵元之间的相位差，当i=0时表示信号，当i=1，2，…，P 时表示干扰；而si（t）表示第i个信号或干扰的复包络；而nk（t）表示第k个阵元的接收噪声。经过阻塞矩阵预处理变换后，联立阻塞矩阵预处理变换矩阵，得到变换后的信号为

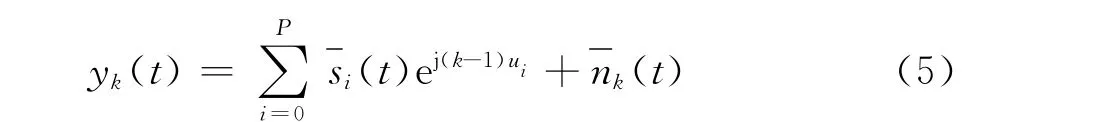
式中:k=0，1，…，N-1（t）=si（t）［1-］；（t）=nk（t）-nk+1（t）.比较式（4）和（5）可以看出，预处理变换改变了信号的复包络，但不改变信号的波达方向，对于主瓣干扰，其复包络（t）等于零。因此，阻塞矩阵预处理变换有效地抑制了主瓣干扰，且不影响后续自适应波束形成处理对其他副瓣干扰零陷的形成。当然，预处理变换损失了一个天线单元的自由度。

在文献［4］中:提出了首先对接收信号进行预处理变换，第二步就是进行常规的自适应波束形成，而且变换后的信号协方差矩阵为

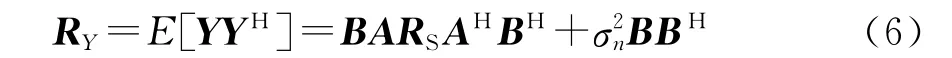
式中:A为阵列的导向矢量矩阵；RS为信号协方差矩阵；为阵列噪声协方差。再利用经典的最优权矢量求解算法可得

式中:μ为一常数；aq为目标信号的导向矢量。文献［4］中还提到，如果直接按照上式进行自适应波束形成，虽然能够克服由主瓣干扰引起的主波束变形、峰值偏移及副瓣电平增高等问题，但会产生新的主波束偏移。其分析这种新的偏移是由预处理变换矩阵B引起的，因此，文献［4］中提出了对其自适应权矢量进行权系数补偿，即

显然权矢量补偿的实质是给原来的导向矢量aq乘上BBH，即利用（BBH）aq代替了导向矢量aq.

下面将给出以上问题的解决方法。

2.主瓣干扰抑制后的方向图保形

通过深入分析文献［4］中提出的基于阻塞矩阵抑制主瓣干扰的实现方法可知:阵列接收数据乘以阻塞矩阵后，按照表达式（5），预处理有效抑制了主瓣干扰，但是其它信号和干扰的复包络改变了，而信号的波达方向没有改变。如果按照该思路，可以对阻塞矩阵预处理后的阵列处理分析如下。

对式（5）进行完整表示，可得

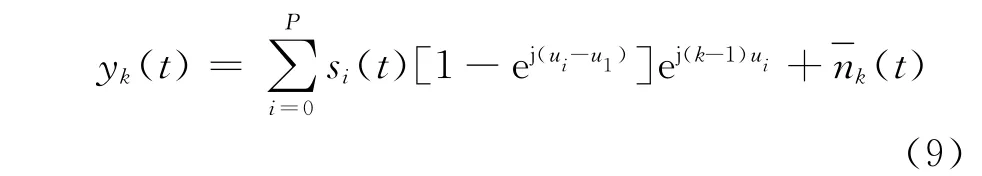
对于主瓣干扰，即当i=1时，由于1-=0，故此处可以不考虑该干扰信号，而且利用上面的表达式也不影响阵列接收数据的描述。因此，信号和剩余干扰经阻塞矩阵预处理后的阵列接收数据也可以用矩阵表示为

式中S1表示除去主瓣干扰后的信号和剩余干扰矢量，但其复包络已经变为si（t）［1-］；A1表示相应的信号和剩余干扰的导向矢量组成的阵列导向矢量矩阵；n1为变换后的阵列接收噪声；Y1为经阻塞矩阵预处理后的阵列接收数据，其实Y1与前面的Y相同，为方便分析在符号上进行了统一，即

由于经预处理，信号的波达方向不变，但损失一个天线单元的自由度，预处理后信号和剩余干扰的导向矢量相对于未处理的导向矢量少了一维，而其它导向矢量参数未变。如果假设空间的电磁信号只有信号和剩余干扰，但现在利用接收阵列的前面N-1个天线进行自适应阵列处理，则相应的阵列接收信号为

显然有

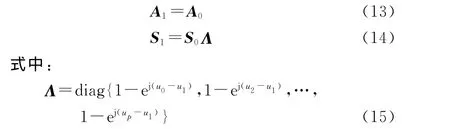
因此有

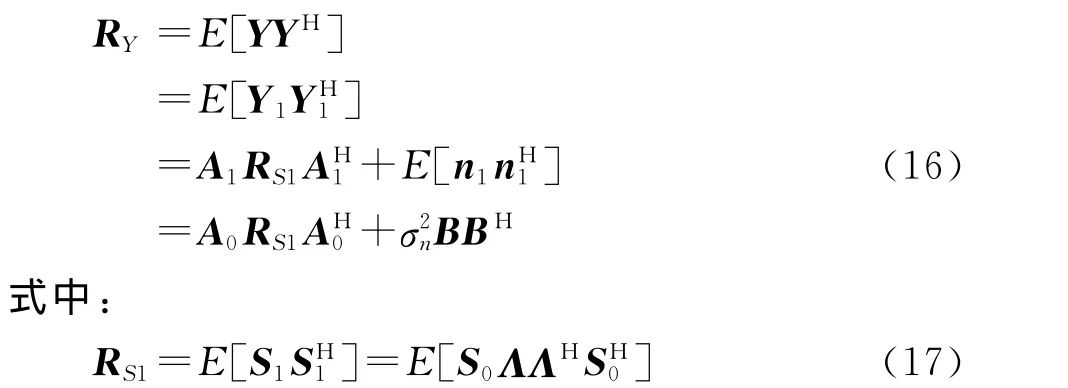
同理有

式中，I为单位矩阵，而

通过对比RY与RY0的表达式可知:两者不论在信号和干扰的协方差矩阵项，还是在噪声的协方差矩阵项，都具有一定的差别。由于两者在自适应波束形成过程中所用的导向矢量相同，而阵列协方差矩阵不同，因此，阵列处理结果的差别可想而知。相比于利用理想协方差矩阵RY0求解权矢量而言，文献［4］中利用式（7）求解自适应权矢量时，相当于在自适应波束形成过程中存在协方差矩阵失配，或称为误差，因而也就出现了主瓣偏离目标方向的结果。而且通过以上分析可知:文献中所提出的权系数补偿也很难取得预期的效果。为克服文献［4］所提算法的缺点，提出利用对角加载来克服波束形成算法的方向图指向偏移问题，同时使得方向图的干扰置零性能下降，故又提出利用线性约束来改善对其它干扰的置零性能。

2.1 利用对角加载改善波束指向性能

对角加载是一种常用的波束形成技术，对有些不能确定的问题，如样本数量小于自由度时，对角加载可以使波束形成问题得以解决，因为此时的样本协方差矩阵将是不可逆的［9］。而且众所周知，对角加载可以增加波束形成器的稳健性。对角加载提供了抵抗到达角失配的稳健性，以及阵元位置、增益和相位扰动的稳健性，还可以抑制由于有限样本支持所引起的协方差矩阵失配。对角加载还可作为一种降维方法，它可以屏蔽掉与小特征值对应的特征矢量的影响，进而降低了自适应自由度的数量。

对角加载就是给协方差矩阵增加一个如下形式的对角矩阵

式中用于控制加载量，称为加载电平。

对角加载的核心和关键是确定加载电平，加载电平的最终选择也是根据自适应波束形成算法最终目标来确定的。如果加载电平取值比较小，则加载的性能与没有加载时的情形相似，反之，如果加载电平较高，则性能和非自适应时的情形相同（即:秩为1）。这是由于加载屏蔽掉了所有自适应自由度。在自适应阵列信号处理中，最优的加载电平通常高于背景噪声平均功率值，但是低于信号和干扰的功率值。一种在信号处理中的经验选择方法是选择加载电平高于背景噪声的5～10dB.

由于对角加载的目的是改善主波束的指向，当加载量较小时，改善不明显，当加载量较大时，尽管可以准确指向目标方向，但是干扰的零陷很难对准干扰的真实方向。这些因素使得加载电平的选择比较困难，为此，提出了尽可能将加载电平选择得比较大，先保证目标方向的准确指向，对于干扰置零问题将利用线性约束进行改善。不仅能够满足预期的方向图要求，同时还使得加载电平的选择变得简单，这是因为，当加载电平选择比较大时，对波束形成算法的性能改善不明显，因而，也相当于为了得到期望的指向性能，相应的加载电平选择范围比较大。

2.2 利用线性约束改善其它干扰抑制性能

为了获得空间某一方向的信号，而使得其它信号的输出最小，可以利用线性约束最小功率（LCMP）波束形成器实现。而LCMP波束形成器的加权矢量是通过使波束形成器在形如CHw=f的一系列线性约束条件下，输出的功率最小来求解的，其中C为P×（N-1）维的约束矩阵，f为P×1维的约束值矢量［10］。

LCMP最优化问题可以描述如下

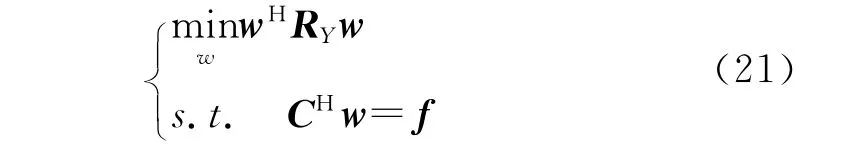
该最优化问题可以利用Lagrange乘数方法进行准确的求解，其最优加权矢量的表达式为

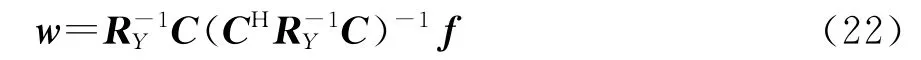
当利用对角加载技术时，相应的权矢量为

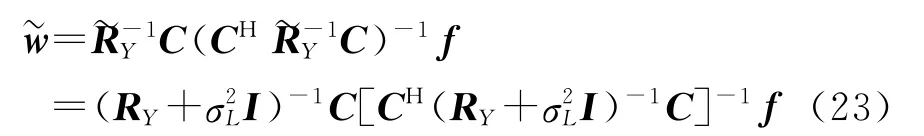
通过对预处理后的数据进行线性约束最小功率自适应波束形成，同时再利用对角加载技术，既可以使波束指向目标方向，同时在干扰方向形成较深的零陷。重要的是，所提出的方法不仅有较好的主瓣干扰抑制性能，同时使得自适应算法的性能达到最优，而且对角加载电平的选择非常简单。

3.仿真分析

为了验证所提方法的正确性和有效性，仿真分析如下。假设天线阵为等距线阵，阵元数N=8，阵元间距为半波长，阵列采样K=1024.其中，信号的方位角θ0=0°，三个互不相关的干扰信号方位角为θi=［5，-30，40］°，信噪比SNR=10dB，而干噪比INR=［10，10，10］dB.由于主波束零点宽度约为20°，故θi=5°的干扰位于主波束内。

3.1 有效性分析

图1给出了预处理前后MUSIC空间谱估计的处理结果。其中“MUSIC”表示预处理前的MUSIC处理结果，而“PreProcess MUSIC”表示预处理后的MUSIC处理结果。显然，预处理有效地消除了主瓣内的干扰，而且处理前后都能有效实现信号和干扰方位的准确估计。

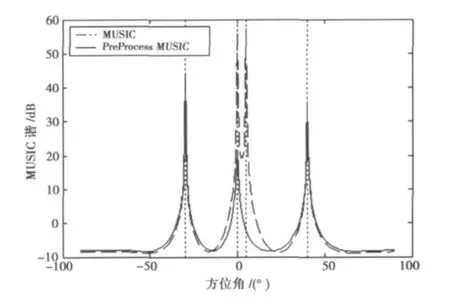
图1 MUSIC空间谱估计

图2给出了自适应方向图比较结果。其中“Capon”表示预处理前的Capon方向图，“PreProcess”表示预处理后的方向图，“PP Compensation”表示预处理并进行权矢量补偿的阵列方向图，“PP Diagonal Loading”表示预处理与对角加载相结合的方向图，“PP DL and Linear Constraint”表示预处理与对角加载和线性约束相结合的阵列方向图，其中的加载电平选择为最大特征值的100倍。由图可知:由于在主瓣内存在干扰，常规Capon所生成的自适应方向图在主瓣内形成了一个深的零陷，导致主瓣严重变形、峰值偏移。而基于数据预处理后的Capon方向图抑制了主瓣干扰，但是方向图具有较大的偏移，加权矢量补偿后的结果更差。通过对预处理后的自适应波束形成进行对角加载可以很好地克服主瓣偏移，但是干扰置零的性能较差，在预处理后将对角加载和线性约束相结合，不仅可以很好地实现主瓣干扰的抑制，可以实现波束的准确指向和干扰置零。

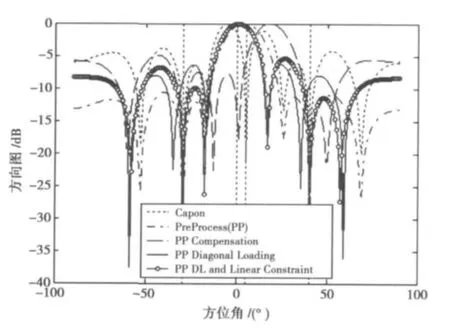
图2 自适应波束形成方向图

为了进一步验证所提算法的正确性，阵列设置同前，而信号和干扰的方位角分别改为θ0=-10°，θi=［-5，-40，30］°.相应的空间谱估计和自适应方向图也能够实现预期的处理效果。因此，所提方法是正确的、有效的。

3.2 渐进性分析

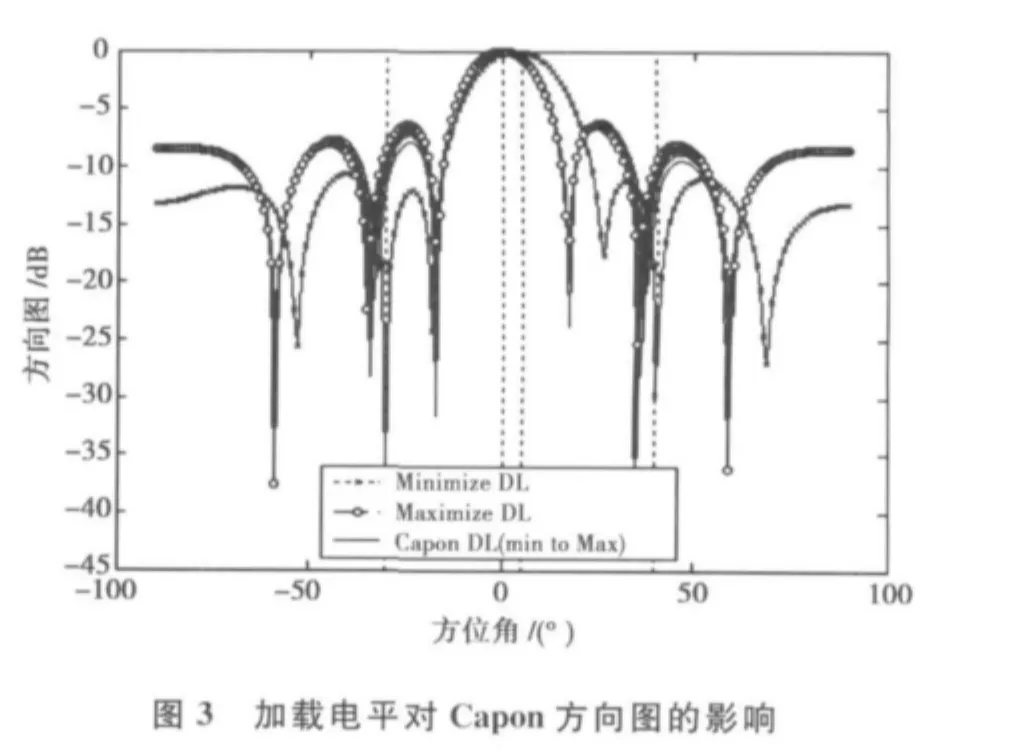
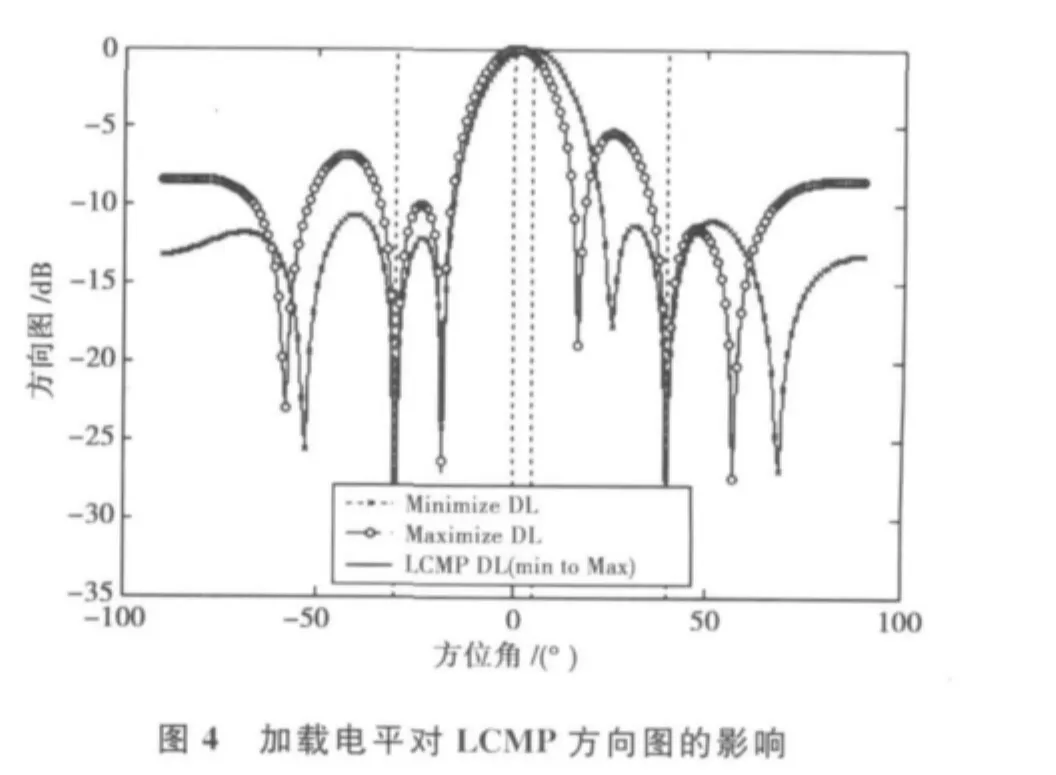
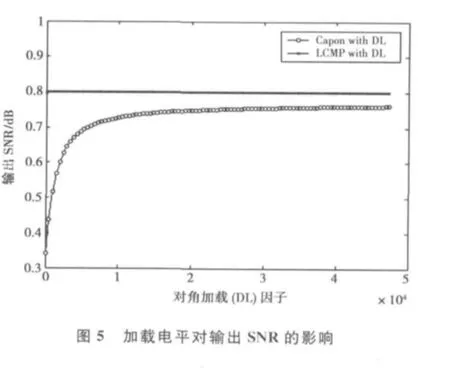
为了分析对角加载对所提方法的性能影响，图3和图4分别给出了加载电平的选择对预处理后的Capon波束形成算法和线性约束最小功率波束形成算法（LCMP）的方向图影响，而图5给出了相应自适应波束形成器的输出信噪比的变化曲线。在图3和图4中，“Minimize DL”表示加载电平取最小值时的方向图，而“Maximize DL”表示加载电平取最大值时的方向图，而“Capon DL（Min to Max）”表示Capon波束形成算法在加载电平取最大和最小值之间的数值时的方向图，而“LCMP DL （Min to Max）”表示LCMP波束形成算法在加载电平取最大和最小值之间的数值时的方向图，其中最小加载电平为0，最大加载电平为最大特征值的100倍。在图5中，“Capon with DL”表示Capon波束形成算法当加载电平在最大和最小值之间的取值时相应的输出SNR，而“LCMP with DL”的意义与其类似。

从图3和图4可以看出:对角加载对预处理后的Capon波束形成算法具有较大的影响，但是随着加载电平的增加，方向图的变化不是很明显，波束形成器的输出SNR也趋于恒定。然而对于预处理后的线性约束最小功率波束形成算法（LCMP），对角加载对方向图的影响不大，输出SNR也变化不大。因此，对于所提方法，加载电平的选择可以比较容易。

4.结 论

针对基于阻塞矩阵实现主瓣干扰抑制中的波束指向偏移问题，通过深入分析阻塞矩阵预处理过程和处理前后的自适应波束形成过程，发现预处理后的自适应波束形成过程中具有协方差矩阵失配，因而引起了相应的波束指向偏移。为此提出了对预处理后的自适应波束形成应用对角加载和线性约束以改善主瓣干扰的抑制效果，同时实现波束的准确指向和其它干扰置零。其中还深入分析了加载电平对所提算法的影响，得出了所提算法对加载电平的选取不敏感，也使所提出算法的应用变得简单而有效。

［1］THEIL A.On combining adaptive nulling with high resolution angle estimation under main lobe interference conditions［J］.IEEE Aerospace and Electronic Systems Magazine，1990，5（11）:16-18.

［2］HUGHES D T，MCWHIRTER J G.Using the penalty function to cope with mainbeam jammers［C］／／The Proceesings of 3rd International Conference on Signal Processing，Beijing China，IEEE，14-18Oct 1996:461-464.

［3］SU Baowei，WANG Yongliang，ZHOU Liangzhu.A mainlobe interference canceling method［C］／／ 2005 IEEE International Symposium on Microwave，Antenna，Propagation and ECM Technologies for Wireless Communications Proceedings.Beijing China，IEEE，8-12Aug 2005:23-26.

［4］李荣锋，王永良，万山虎.主瓣干扰下自适应方向图保形方法的研究［J］.现代雷达，2002，24（3）:50-55.LI Rongfeng，WANG Yongliang，WAN Shanhu.Research of reshaping adapted pattern under mainlobe interference conditions［J］.Modern Radar，2002，24（3）:50-55.（in Chinese）

［5］胡 航，张 皓，宗成阁，等.子阵级自适应单脉冲的四通道主瓣干扰抑制［J］.电波科学学报，2009，24（5）:820-826.HU Hang，ZHANG Hao，ZONG Chengge，et al.Four-channel mainlobe jamming suppression for adaptive monopulse at subarray level［J］.Chinese Journal of Radio Science，2009，24（5）:820-826.（in Chinese）

［6］陈希信，韩彦明，于景兰.高频雷达自适应波束形成抗干扰研究［J］.电波科学学报，2010，25（6）:1169-1176.CHEN Xixin，HAN Yanming，YU Jinglan.Research for interference suppression in HF radar based on ADBF［J］.Chinese Journal of Radio Science，2010，25（6）:1169-1176.（in Chinese）

［7］覃 岭，黄 茜，李会勇，等.主瓣干扰下宽带圆阵自适应波束形成方法［J］.电子科技大学学报，2009，38（3）:359-353.QIN Ling，HUANG Qian，LI Huiyong，et al.Adaptive broadband beamforming of circular array under main lobe interference condition［J］.Journal of University of Electronic Science and Technology of China，2009，38（3）:359-353.（in Chinese）

［8］宋立众，乔小林，吴 群.一种基于极化DBF的制导雷达抗干扰方法［J］.电波科学学报，2010，25（1）:109-117.SONG Lizhong，QIAO Xiaolin，WU Qun.Method of interference suppression based on polarization digital beam formation for the guidance radar［J］.Chinese Journal of Radio Science，2010，25（1）:109-117.（in Chinese）

［9］刘聪锋，廖桂生.基于对角加载的STAP性能改善［J］.电子与信息学报，2008，30（3）:906-910.LIU Congfeng，LIAO Guisheng.Improving the STAP Performance via Diagonal Loading［J］.Journal of Electronics ＆Information Technology，2008，30（3）:906-910.（in Chinese）

［10］刘聪锋，廖桂生.宽带接收机的窄带信号频率、二维角度估计新方法［J］.电子学报，2009，37（3）:523-528.LIU Congfeng，LIAO Guisheng.Novel Method of Narrow Band Signal Frequency and 2DAngle Estimation for Wide Band Receiver［J］.Acta Electronica Sinica，2009，37（3）:523-528.（in Chinese）