改进FSVM在发动机振动故障融合分析中的应用
费成巍,白广忱
随着航空发动机的推力、转速、动强度等日益提高,发动机零部件的振动载荷不断增加,振动引起的故障越来越受到关注,对于航空发动机整机而言,振动故障诊断问题一直是学术界和工程技术领域研究的热点问题之一[1-2]。在众多故障诊断方法中,一直受欢迎的支持向量机(Support Vector Machine,SVM)理论的发展出现了瓶颈,因为含有噪声与野值干扰的样本在特征空间中总位于分类面附近,造成了最优分类面的确定模糊性,往往导致所获得的分类面不是真正的最优分类面[3-4]。为了解决该问题,大量学者融合了模糊理论和SVM理论的优点,将隶属度概念引入SVM,开始研究模糊支持向量机(Fuzzy Support Vector Machine,FSVM)方法[4-7]。该方法是采用对不同的样本赋予不同的惩罚权系数,以便根据不同样本有不同贡献原则构造目标函数,对含有噪声与野值的样本赋予较小的权值,这样就可以大大降低了噪声与野值的影响。然而,隶属度函数的设计是整个FSVM理论算法的关键,不同的隶属度函数会对算法的处理结果以及算法实现的难易程度产生不同的影响[4-5],这要求隶属度函数必须能客观、准确、有效地反映系统中样本存在的不确定性。目前,在FSVM方法中主要采用样本到类中心之间的距离来度量其隶属度大小,该方法不能很好地区分有效样本中含有噪声或野值样本[6-7]。
针对上述存在的问题和航空发动机整机振动故障信息的特点,本文在确定模糊隶属度时不仅考虑了样本与类中心之间的关系,还考虑了类中各个样本之间的关系,能有效地将支持向量与含噪声或野值样本区分开。通过实例计算与分析检验该方法在航空发动机整机振动故障分析中的有效性和准确性。
1 模糊支持向量机
与常规SVM相比,FSVM的样本除了特征与类属标识外,还增加了隶属度一项。下面对2类分类情况进行讨论。
设训练样本集为{[x1,y1,μ(x1)],…,[xn,yn,μ(xn)]}和核函数为 K(xi,xj),其中,xi∈RN,类标识为yi∈{-1,1}及隶属度为 0< μ(xi)≤1。K 对应某特征空间 Z 的内积,即 K(xi,xj)=〈 φ(xi),φ(xj)〉,变换 φ:X→Z将训练样本从原始模式空间RN映射到高维特征空间Z之间的映射关系,μ(xi)为训练样本xi属于yi的隶属度。
由于隶属度μ(xi)表示该样本属于第i类的可靠程度,ξi是SVM目标函数中分类的误差项,则μ(xi)ξi为带权的误差项,由文献[8]得到最优分类面为下面目标函数的最优解。
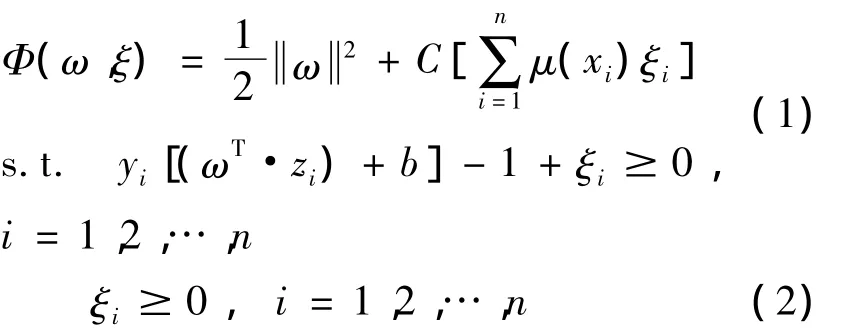
式中:ω为超平面的法向量,C为惩罚因子常数,b为超平面的偏置,ξi是松弛变量。由式(1)可知,当μ(xi)值变小时减小了ξi在式(1)中的影响,导致相应的xi为不重要的样本。
则相应最优分类面的判别函数式(也称分类器)为:
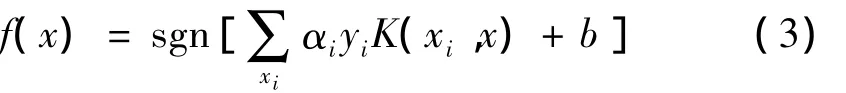
式中:K(xi,xj)称为核函数,包括多项式函数、Sigmoid函数、高斯径向基函数(Gaussian Radial Base Function,GRBF),其中GRBF对应的特征空间是无穷维的,且比其它核函数有效,受到普遍使用。αi的条件为下式:
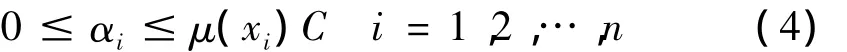
αi>0对应样本xi为支持向量,支持向量有两种类型:一种是满足0≤αi≤μ(xi)C条件的支持向量xi位于分类面附近;另一种是满足αi=μ(xi)C条件的支持向量xi为错误分类样本。FSVM与SVM方法的差别在于在FSVM中含有隶属度μ(xi),若同一个αi值的样本xi在两种方法中可能属于不同类型的支持向量。参数C是一个自定义的惩罚因子,对不同样本的隶属度赋予不同的C值可以达到对不同的样本采用不同程度的惩罚作用[8]。
2 隶属度的确定
2.1 传统隶属度确定方法
在SVM方法中,最优分类面主要由支持向量决定,支持向量位于类边缘,而野值或含噪声的样本常常也位于类边缘附近,例如含有野值或噪声样本的支持向量如图1所示。前人已经研究了利用距离和S函数来解决以上问题,确定有效的隶属度函数[7,9],由于这两种方法都是依据样本到类中心之间的距离确定样本的隶属度,对类中每个样本都要按照同一种方式进行考虑,对有效样本与含有异常信息样本的分离效果不太好,故不能有效地反映样本的不确定性。

图1 含有野值或噪声样本示意图Fig.1 Diagram of samples with outliers or noise
针对以上问题,引入紧密度来改善隶属度函数,如图2两个不同类中样本之间紧密度的差别。在图2(a)与(b)中,样本x到它们所在类中心之间的距离相等,若仅依据距离来确定隶属度则两者的隶属度相同。然而,若考虑图2(a)中样本x与类中其他样本之间的距离远小于图2(b)中的距离这一情况,那么图2(a)中样本x属于所在类的隶属度应大于图2(b)中的。

图2 两个不同类中样本之间紧密度的差别示意图Fig.2 Affinity contrast from two classified samples
2.2 隶属度确定函数的改进
针对以上情况,尝试在确定样本的隶属度时,充分考虑样本到所在类中心之间的距离和样本与类中其他样本之间的关系,然而样本与类中其他样本之间的关系可通过类中样本的紧密度来反映,每种类别对应一个球,于是可以得到训练支持向量机的k个球(am,Rm),其中am是包围m类样本球的球心,Rm为球的半径,称这种方法为球紧密度隶属度确定方法。
由上述分析可得到球紧密度FSVM的隶属度函数[10]定义如下:
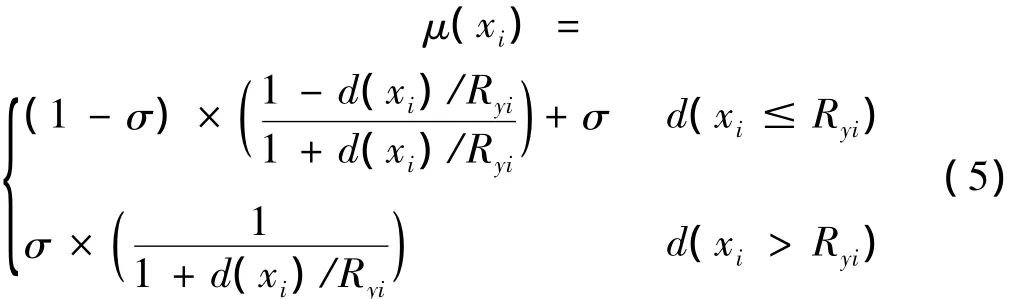
式中:d(xi)= φ(xi-ayi),σ∈(0,1)。关于 σ 的取值,本文利用交叉确认的方法获得它的最优值,即对应FSVM分类精度最高时的σ值。
3 FSVM诊断方法的数学模型
航空发动机整机振动故障是多类故障诊断问题,需要建立多类SVM分类器。对于多分类问题,常用算法有一对多组合(one against rest,1-a-r)方法、一对一组合(one against one,1-a-l)方法和有向非循环图法 SVM(Direeted Acyclic Graph SVM,DAGSVM)方法[11]。FSVM多分类问题是在这些方法的基础上,构造隶属函数以减少不可分区域,达到解决问题的目的。同理,将其推广到FSVM的第一种形式,便得到了基于1-a-a的FSVM多分类算法。
在这种算法中,对于一个k类分类问题有训练样本如下:

式中:xi∈RN;yi∈{1,2,…,k};0 < μ(xi)≤1。
定义1:对于 RN上的一类点{x1,x2,…,xn},记 xc为类中心点,r为类半径。其中:

根据一对多组合思想进行分类,即依次训练k个两类分类器,并且每次训练过程都是引入模糊性的(即事先为每个样本xi生成一个模糊隶属度μ(xi))。假如现在要将第l类和剩余样本分开,根据上述定义易得到第l类的中心点(记为x+),类半径记为r+;将剩余样本看做另一类,其中心点记为x-,类半径记为 r-。引入一个充分小的δ避免μ(xi)=0,因此,模糊隶属度μ(xi)可定义为:
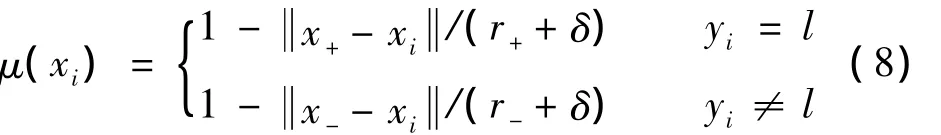
接下来进行FSVM的训练过程,每次可得一个两类分类器。当所有训练结束时,根据式(3)可以得到k个两类最优分类器:

对于新给的测试样本x被分入:

依照上述步骤可以有效地对多类的故障样本进行分析和分类。
4 实例计算与分析
4.1 参数选择和故障分析流程图
本文以航空发动机整机为研究对象,振动数据来源于某航空发动机研究单位台架试验数据库里的5个典型截面的9个垂直和水平方向振动数据,5个典型截面划分[2]如表1所示。

表1 航空发动机整机振动测点位置选择Tab.1 Location choice of the Aero-engine whole-body vibration measuring point
这些振动数据包括台架松动、动静碰磨、轴系不对中和转子不平衡4种典型故障的大量数据,并对数据进行整理和分析之后,每个测点选取了包括4种典型故障的40组数据,共360组数据,有9个训练样本集。将此数据经过预处理后形成高维空间向量,利用信息增益的方法进行特征降维,向量中的每个权重根据极值原理求得。FSVM模型中,本文选择GRBF核函数,高斯分布宽度参数δ取4,惩罚参数C取361。利用交叉确认的方式找出σ的最优值为0.8,此时对应 FSVM的最高诊断正确率为94.81%。图3给出了不同的σ值对紧密度FSVM对数据样本正确分类的影响。

图3 不同的σ值相对应紧密度FSVM分类的正确率Fig.3 Classified accurate rate of affinity FSVM to σ
4.2 模糊支持向量机故障分析
在基于FSVM的航空发动机整机振动故障分析过程中,本文以故障的诊断为例进行故障分析,先用9个测点的90组(即每个测点选取10组,包括4种典型故障的数据)训练样本建立FSVM诊断模型,再将每个测点剩余的30组测试样本输入FSVM网络训练模型,然后采用决策规则对该模型的输出进行判断,确定样本所属的类别。为检验基于紧密度FSVM故障诊断方法的有效性,基于相同的诊断样本,分别采用BP神经网络、传统SVM、基于类中心距FSVM进行了故障诊断,其结果如表2所示。

表2 航空发动机整机振动故障诊断结果及比较Tab.2 Diagnosis results and their comparison of aeroengine whole-body vibration fault

表3 有噪声干扰条件下的诊断结果Tab.3 Diagnostic results with noise interference
从计算结果可以看出,BP神经网络诊断结果最差,正确率仅为81.85%,这说明在小样本情况下,神经网络诊断方法不如SVM诊断方法有效;其他三种方法诊断结果相比较,基于紧密度FSVM的故障诊断准确率(90.37%)比常规SVM故障诊断准确率(85.93%)和基于类中心距FSVM诊断准确率(87.41%)明显提高,验证了基于紧密度隶属度FSVM的故障诊断方法的有效性和可行性。
4.3 紧密度FSVM抗噪声能力检验
为了检验基于紧密度FSVM诊断系统在有噪声干扰条件下的诊断能力,给输入数据叠加信噪比为2的高斯白噪声信号,经诊断后得到分类正确率为88.33%;为了体现出基于紧密度FSVM的抗噪声能力,基于同样的诊断样本和叠加相同的噪声,也分别利用SVM和类中心距FSVM进行故障分析,其结果如表3所示。由表3可以看出:在强噪声干扰情况下,基于紧密度FSVM的诊断正确率能达到88.33%,而传统SVM和类中心距FSVM的诊断精确度分别为83.06%和85.83%。紧密度FSVM诊断精度虽然没有无噪声干扰情况下的诊断精确度高,但仍然明显优于SVM和类中心距FSVM的诊断精确度,可见在强噪声干扰情况下基于紧密度FSVM诊断系统仍能对输入样本很好地分类,这说明FSVM具有很强的鲁棒性和容错能力。
5 结论
(1)针对航空发动机整机振动故障信息不确定性、模糊性和故障样本缺乏的突出问题,对FSVM传统的隶属度确定函数进行改进,介绍了基于紧密度函数的隶属度确定方法。
(2)将FSVM融合分析方法应用到航空发动机整机振动故障诊断中。首先通过交叉验证的方法确定FSVM理论中σ的最优值;再通过实例计算与分析,验证了无论在无噪声干扰情况下还是在有强噪声干扰下该方法故障诊断正确率比采用BP神经网络方法、SVM方法和类中心距FSVM方法的正确率高,显示了强大的分类性能和抗噪性能力的优点。在一定程度上为航空发动机整机振动故障有效、准确地诊断与分析提供了一种新的方法。
[1]费成巍,艾延廷.航空发动机健康管理系统设计技术[J].航空发动机,2009,35(5):24-29.
[2]费成巍,艾延廷,王 蕾,等.基于支持向量机的航空发动机整机振动故障诊断技术研究[J].沈阳航空工业学院学报,2010,27(2):29-33.
[3] Ding W D,Yuan J Q.Spike sorting based on multi-class support vector machine with super position resolution [J].Medical & Biological Engineering & Computing,2008,46(5):139-145.
[4] Liu Y H,Huang H P.Fuzzy support vector machines for pattern recognition and data mining[J].Internation Journal of Fuzzy Systems,2002,4(3):826-835.
[5]Mao Y,Xia Z,Yin Z,et al.Fault diagnosis based on fuzzy support vector machine with parameter tuning and feature selection[J].Chinese Journal of Chemical Engineering,2009,15(2):233-239.
[6]张 翔,肖小玲,徐光祐.模糊支持向量机中的隶属度的确定与分析[J].中国图像图形学报,2009,11(8):1188-1192.
[7] Lin CF,Wang SD.Fuzzy support vector machines[J].IEEE Transactions on Neural Networks,2002,13(2):464-471.
[8]张秋余,竭 洋,李 凯.模糊支持向量机中隶属度确定新方法[J].兰州理工大学学报,2009,35(4):89-93.
[9] Bian Z Q,Zhang X G.Pattern recognition[M].Beijing:Tsinghua University Press,2000.
[10]艾 青,秦玉平,方 辉,等.一种扩展的紧密度模糊支持向量机及其在文本分类中的应用[J].计算机应用与软件,2010,27(4):45-47.
[11]刘泰安,梁永全,薛 辛.一种新的模糊支持向量机多分类算法[J].计算机应用研究,2008,25(7):2041-204.

