海洋波力发电倒置摆系统的非线性振动实验研究

陈恩利，田瑞兰，郜浩冬

作为人类可利用的清洁能源，海洋能源由于资源丰富、清洁环保、可再生性强等特点，被联合国环境组织视为目前最理想、最有前景的替代能源之一。我国海洋资源丰富，近海域波浪的蕴藏量约为1.5×108kW，可利用价值极高。同时，我国又是世界能源消费大国，因此，研究开发新型海洋波力能源发电系统意义十分重大。

目前，研究最多的海洋波力装置有三种:利用波浪压力变化的振荡水柱波能装置;利用物体在波浪作用下的振荡和摇摆运动的摆式波能装置;利用波浪的沿岸爬升将波浪能转换成水的势能的聚波水库波能装置。而本项目研究的倒置摆发电装置具有系统简便、实用性强、可独立稳定发电的明显优势，有广阔的应用前景。

本文通过倒置摆的非线性振动实验，研究该系统在海洋发电应用中的可行性及实现条件。目前，研究非线性系统动力学行为的方法通常有解析法、数值法和实验法。由于很难得到系统方程的精确解析解，应用数值方法又不可避免地存在截断误差和舍入误差，因此，越来越多的研究者尝试将实验法与解析法、数值法相结合研究非线性系统的动力学行为。文献［1］从理论和实验研究了T型梁－质量块3自由度模型的非线性动力学行为，观察到了一些理论上没有解释的现象。文献［2］将一根钨丝作为悬索模型，在磁场中通以正弦电流进行激励，实验观察到了大幅激励下弦的分岔过程:周期运动－准周期运动－混沌运动－准周期运动－周期运动。文献［3］将尼龙绳作为悬索模型观测了稳态的准周期运动、锁相现象和混沌吸引子。文献［4］设计了一个L型梁－质量块模型，实验观察到了跳跃现象和能量在两个模态之间的不断交换，验证了饱和现象。文献［5］对两柔性梁碰撞振动进行了实验研究，观察到了亚谐、超谐、概周期、混沌现象。文献［6］针对卫星主要结构材料铝质蜂窝板的非线性动力特性进行了振动试验及分析。文献［7］利用实验方法研究粘弹性传动带的非线性振动，得到了粘弹性传动带的频率响应曲线和周期运动、倍周期运动以及混沌运动的波形图和相图。上述实验研究不但从宏观上展示非线性现象的存在，为非线性动力学理论提供易于感知的、直观和精确的实例，而且促使研究者发展新的分析方法来处理观察到的新非线性现象。

关于倒置摆的实验问题，国内外学者大部分都侧重于单摆(基座不动)运动，或单摆及双摆运动控制实验，控制实验主要通过在摆杆底部提供相反运动保持摆杆直立状态。文献［8］利用实验验证了应用二次型性能和指标最优控制的方法设计控制规律的可行性。文献［9］实现了四级单摆的实物控制系统。文献［10］设计并制作了受周期外力驱动的单摆演示实验装置。

图1所示为本文提出的海洋波力发电装置的结构示意图。海洋上漂浮的船舶作为一个简谐振动的基座，其上固定一根刚性摆杆，末端固定一个不计摩擦的连接点与小船相连构成一个倒置摆。将该模型简化为一个简单的具有振动基座的倒置摆(如图2所示)，其方程为:

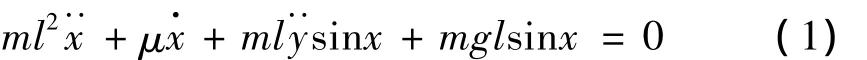
其中:x为倒置摆运动的角位移，l为摆长，m为小球的质量，μ为系统的阻尼系数。

文献［11］利用数值模拟证明了系统(1)存在稳定解，并从理论上揭示出系统(1)随激励频率的变化具有丰富的动力学行为。本文利用振动台模拟海洋波动，通过改变振动台的激励频率、幅值模拟海浪的波幅及频率，进行海洋波力发电倒置摆的实验研究。该装置不仅存在大周期转动、稳定振动现象，而且存在1/2共振下的周期运动和1/4共振下的周期运动。研究结果证明倒置摆系统可以利用其非线性系统，通过一定的系统设计，实现发电需要的大周期转动，为海洋波力发电的可行性奠定实验基础。

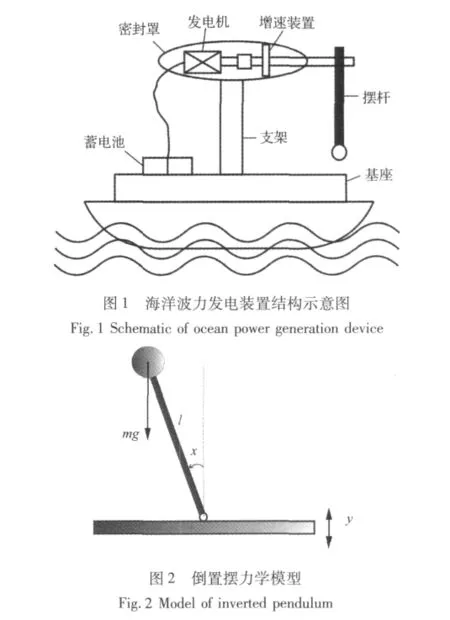
1 实验方案与装置

其中:ω是振动台的激励频率，α是振动台的激励振幅。实验路线如下:

(1)激励闭环控制系统:由PUMA控制仪，ES－10振动台共同构成激励闭环控制系统，控制仪输出定幅扫频信号，该信号驱动功率放大器输出大功率信号推动振动台做正弦运动。振动台上设有压电加速度传感器，传感器采集振动台的振动信号输入控制仪，控制仪将输出信号与输入信号进行比较，从而构成闭环系统，保证振动台的精确简谐振动。

(2)实验对象:安装在振动台上的倒置摆系统，转轴处安装有高润滑的滚动轴承，减小阻尼的影响。

(3)角位移精确采集系统:倒置摆转轴处安装有高精密角位移传感器，传感器采集转角随时间变化的电压信号，通过专用设计A/D采集系统，将转动电压信号转变为角位移时域信号输入INV306DF采集系统，这样可以对振动台的激励信号和倒置摆振动信号同时采集，保证振动信号的同步性和实验数据的有效性。

实验装置图见图3、图4所示，实验框图见图5。实验中的倒置摆由一个轻质杆和一个在杆端固定的小球组成，杆长 0.11 m，杆质量 6.2 g，小球质量 11.5 g。

2 倒置摆实验方法

2.1 阻尼和固有频率的确定

研究倒置摆的振动问题，需要确定该系统的阻尼和固有频率。由于大幅振动的倒置摆具有非线性振动特性，为此通过自由衰减振动实验确定在不同振幅下系统相应的阻尼、固有频率和杆长。文献［1］中模型摆杆为理想无质量的，而实验系统模型中的摆杆具有一定的质量。根据惯性矩平衡原理，可以得出无质量的等效杆长，其计算公式如下:

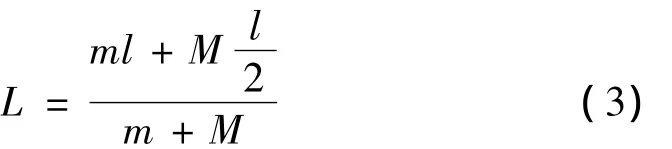
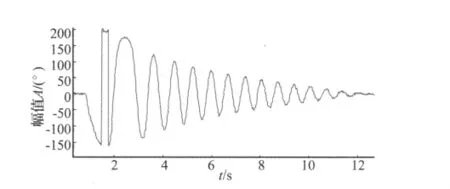
图6 倒置摆振动衰减曲线Fig.6 Vibration decay curve of the inverted pendulum

其中:m为小球质量，M为杆的质量，l为实际杆长。本实验采用的杆长为0.11 m，杆质量为6.2 g，小球质量为11.5 g，故等效杆长为9.6 cm。初位移为150°时倒置摆衰减振动曲线如图6所示，图中A表示振幅。初始位移不同，得到的衰减指数、固有频率及实验换算摆长均不同(见表1所示)，与小位移线性单摆相比可以看出大位移倒置摆表现出很强的非线性特征。

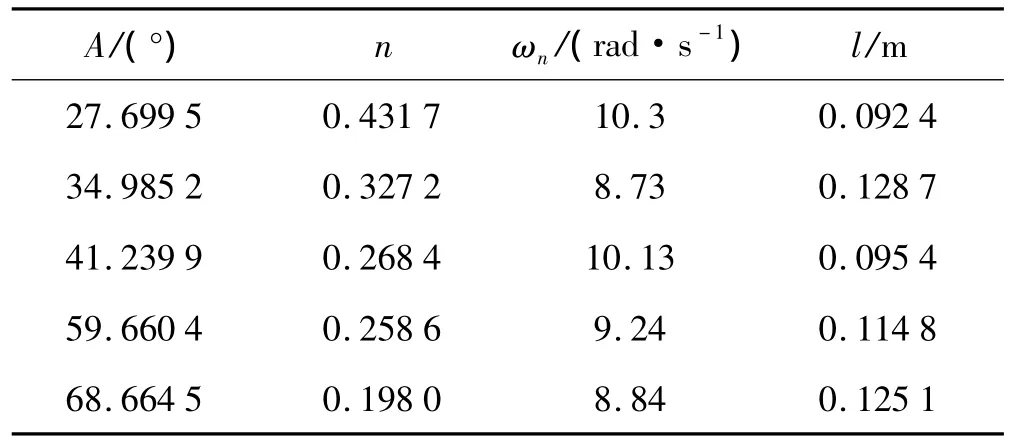
表1 振动衰减实验结果Tab.1 Experimental results of vibration decay

从表1中可以看出:当振幅为41.24°时的实验换算杆长与等效杆长相等，此时对应的衰减指数n=0.268 4，ω0=10.13 rad/s。

图7为实验数据拟合出的倒置摆固有频率随振幅变化的曲线，从图上可以看出随着振幅从20°增大到180°，倒置摆固有频率也由 10.47 Hz降到了 5.324 7 Hz，从而验证倒置摆系统的非线性。

2.2 信号采集

在振动信号测试过程中，倒置摆的振动角位移精确采集十分重要，同时需要控制阻尼大小。本实验中，采用精确角位移传感器并采用高润滑滚动轴承，对角位移及振动台激励同时采样，通过对角位移的数据进行微分处理得到的角速度数据。实验数据一次微分的计算公式为:

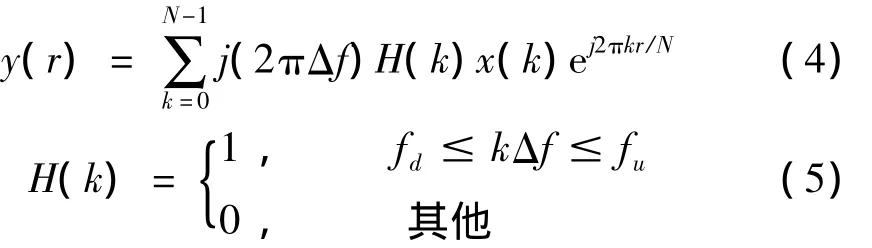
其中:y(r)为微分计算后的速度;x(k)为x(r)的傅里叶变化;Δf为频率分辨率;fd和fu分别为下限截止频率和上限截止频率。

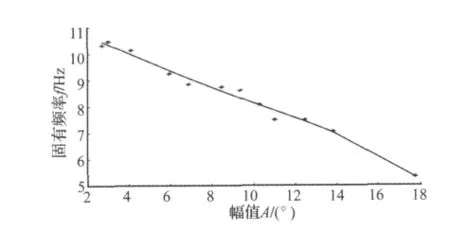
图7 倒置摆软特性曲线Fig.7 Soft characteristics curve of the inverted pendulum

2.3 实验过程

根据实验测得的倒置摆系统阻尼，固有频率等参数，通过Matlab仿真计算，可得倒置摆系统各种非线性现象发生的参数条件。实验时，通过扫频控制改变振动台的输出频率，扫频过程中输出振幅不变。扫频时起始频率为1.5 Hz，截止频率为200 Hz;激励幅值由峰值5 mm逐渐调整至35 mm;通过定幅扫频观察倒置摆的非线性振动特性，依据实验数据进行分析，确定倒置摆的非线性运动形式。为避免偶然性，增加数据的准确性，对临近参数条件下的振动进行多次实验。

3 倒立摆实验数据仿真

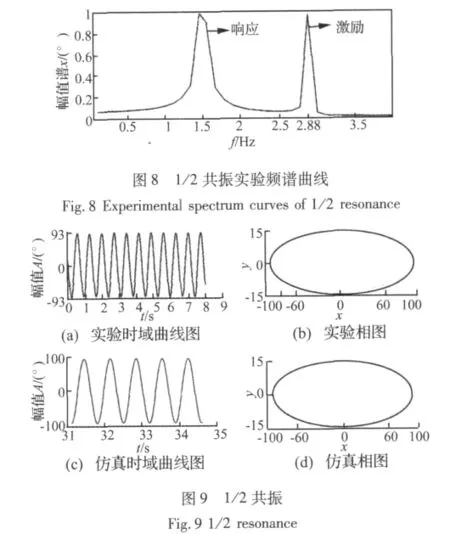
依据数值仿真结果，实验从2 Hz开始扫频。在振动台定幅扫频过程中，观察倒置摆能否在激励下产生稳定的周期运动。图8中显示当振动台激励频率达到2.88 Hz时，倒置摆产生周期运动，此时采集实验数据并处理，得到频谱图(图8)、振动时域图和相图(图9(a)、图9(b))。使用相同的数据通过仿真可以得到振动时域图及相图见图9(c)、图9(d)所示。图中x表示角位移、y为角速度。从图8可知响应频率为1.45 Hz，而此时振动台的激励频率约为2.88 Hz，由此确定此时运动为1/2共振。从图9可以看出实验结果与数值仿真结果非常吻合。

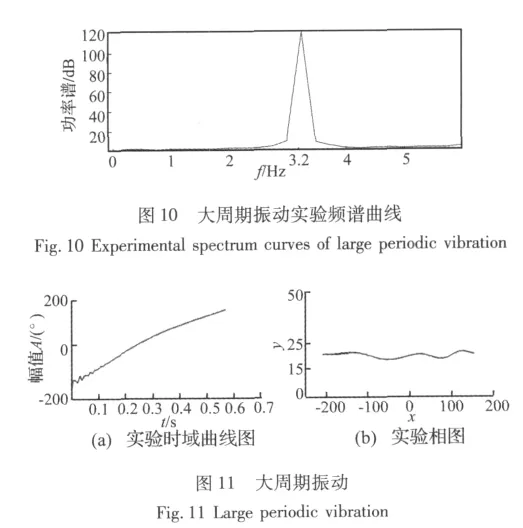
当激励频率达到f=3.2 Hz时，倒置摆出现大周期运动，其实验频谱如图(10)所示、振动实验时域曲线图如图11(a)所示，实验数据画出相图如图11(b)所示，图中A表示振幅。

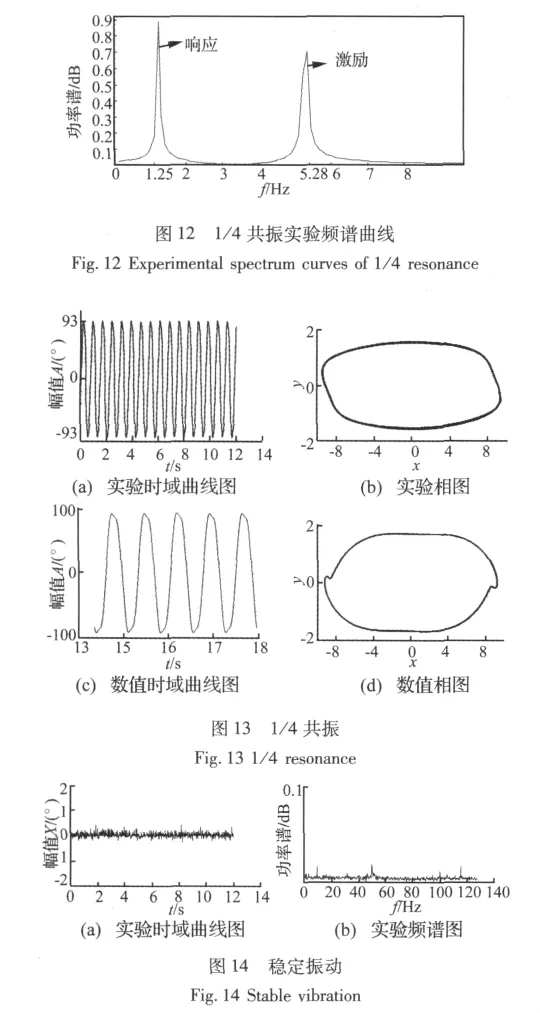
当激励频率从f=3.1 Hz不断增大至f=5.28 Hz时，倒置摆又产生周期运动，实验数据做出的频谱图见图12所示，依据实验数据画出振动时域曲线图和相图(如图13(a)、图13(b)所示)。图13(c)、图13(d)是相对应的数值仿真结果。从图12可以得知响应频率为1.25 Hz。而此时振动台的激励频率为5.28 Hz，由此可以确定此时运动为1/4共振。从图13可以看出实验结果与数值仿真结果非常吻合。

当频率增大至f=15.03 Hz时，倒摆处于0°倒置位置且保持稳定状态，此时对应文献［11］中的稳定吸引子。实验数据画出的时域曲线见图14(a)所示，频谱图见图14(b)所示。

4 结论

本文通过实验方法研究了海洋波力发电倒置摆装置的非线性振动特性，给出了实验条件下产生不同非线性现象的动力学参数，揭示倒置摆系统存在大周期现象、不同共振状态下的周期现象和稳定吸引子现象。实验结果表明，在海洋波力作用下，经过一定的动力学设计，倒置摆发电装置能够实现发电需要的大阻尼条件下的大周期运动。该发电模型具有海浪波能吸收好，输出动力多、消耗少的特点。因此，倒置摆模型在开发利用海洋波力能源发电中具有十分重要的应用开发前景。

［1］ Nayfeh T A，Nayfeh A H，Mook D T.A theoretical and experimental investigation of a three-degree-of-freedom structure［J］.Nonlinear Dynamics，1994，6(3):353－374.

［2］Molteno T C，Tufillaro N B.Torus doubling and chaotic string vibrations:experimental results［J］.Journal of Sound and Vibration，1990，137(2):327－330.

［3］Alaggio R，Rega G.Characterizing bifurcations and classes of motion in the transition to chaos through 3D-tori of a continuous experimental system in solid mechanics［J］.Physica D，2000，137(1):70－93.

［4］ Haddow A G，Barr A D S，Mook D T.Theoretical and experimental study of modal interaction in a two-degree-offreedom structure［J］.Journal of Sound and Vibration，1984，97(3):451－473.

［5］金栋平，胡海岩.两柔性梁碰撞振动类型的实验研究［J］.实验力学，1999，14(2):129－135.

［6］陈昌亚，宋汉文，王德禹，等.卫星结构铝蜂窝板非线性振动试验与参数辨识研究［J］.振动与冲击 2004，23(1):8－11.

［7］张红星，张 伟，姚明辉，等.粘弹性传动带非线性振动实验研究［J］.动力学与控制学报，2007，5(4):361－364.

［8］王晓凯.基于简化模型的倒立摆控制实验研究［J］.计算技术与自动化，1997，16(1):16－19.

［9］李洪兴，苗志宏，王加银.四级倒立摆的变论域自适应模糊控制［J］.中国科学E辑，2002，32(1):65－75.

［10］陈立宏，乔红华，彭建华，等.外周期力驱动的倒摆混沌运动演示仪［J］.物理实验，2005，25(12):34－37.

［11］李向红，崔文良，曹庆杰.倒置数学摆在海洋发电中的应用研究［J］.动力学与控制学报，2009，7(3):252－257.