基于形状记忆合金的新型消能减震装置抗震性能研究

陈 云，吕西林，蒋欢军

现代结构工程中，为了对结构振动进行控制，目前已经开发了多种形式的阻尼器，根据不同类型阻尼器的耗能原理不同，可以分为金属阻尼器、摩擦型阻尼器、黏弹性阻尼器、粘滞阻尼器、调谐质量阻尼系统和调谐液体阻尼系统等［1］。但这些阻尼器均不同程度存在一些缺点，比如粘滞阻尼器对粘滞液体的性能要求很高，而且维护费用和造价较高;粘弹性阻尼器易老化;金属屈服阻尼器产生塑性屈服后变形很难恢复;摩擦型阻尼器在长期应用下的可靠性较差等缺点。

为了克服这些缺点，在土木工程中，利用各种智能材料或机敏材料进行结构的消能减震控制已经成为一个研究的热点。同济大学土木工程防灾国家重点实验室的吕西林和赵斌［1］开发了电流变体智能阻尼墙和磁流变体智能阻尼墙，这两类阻尼器可以实现对结构的主动控制效果;北京工业大学的薛素铎等［2－4］开发了多种不同类型的记忆合金阻尼器;西安建筑科技大学的王社良等［5］也对形状记忆合金在结构工程中的应用做了多方面的探索研究;大连理工大学的欧进萍等［6］也对各种类型的新型阻尼器进行了系统研究，如磁流变液阻尼器、结构压电驱动和压电变摩擦阻尼控制系统以及形状记忆合金被动和主动控制系统。

形状记忆合金(Shape Memory Alloys，SMA)材料是一种新型的机敏材料，它具有两种特别的性能，即形状记忆性能和超弹性性能。

利用形状记忆合金的超弹性和高阻尼特性制作的被动耗能阻尼器可以克服上述其他类型的阻尼器存在的问题，与其他阻尼器相比，形状记忆合金阻尼器具有耐久性和耐腐蚀性能好，使用周期长，可恢复应变大等优点。

国内外也有很多学者［2－12］对采用形状记忆合金丝的阻尼器进行了研究和开发，然而开发设计出一些耗能能力强，同时具有自复位功能，结构形式简单，便于工程应用的被动耗能阻尼器仍是目前面临的实际问题。本文主要对形状记忆合金在框架结构中的应用做一些探索研究。

1 形状记忆合金的力学性能

1.1 形状记忆合金的超弹性本构关系

目前形状记忆合金有多种不同类型的本构关系，这些本构模型都侧重某个方面描述形状记忆合金的性能［5］。

这些不同类型的本构关系都有一些缺点，在具体工程应用时不太方便，为此本文主要介绍ANSYS大型有限元程序自带的形状记忆合金本构模型［13］，并将试验所得的形状记忆合金应力应变曲线进行拟合，从而得到软件计算所需的本构模型参数。

形状记忆合金中，奥氏体所占的百分比用ξA表示，马氏体所占的百分比用ξS表示，满足ξA+ξS=1，这里选择ξS为独立的变量，假定材料为各向同性的，马氏体相和奥氏体相在力作用下的相互转化可以通过Drucker－Prager荷载公式来模拟:

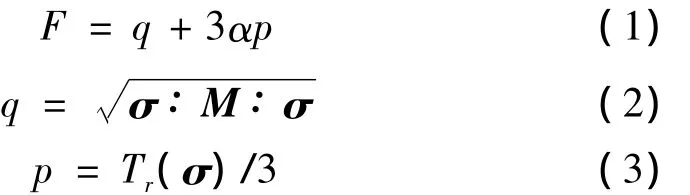
其中:α为材料参数，M为矩阵(式(4))，σ为应力向量，Tr为迹线算子。

马氏体体积含量的变化可以通过如下公式来定义:

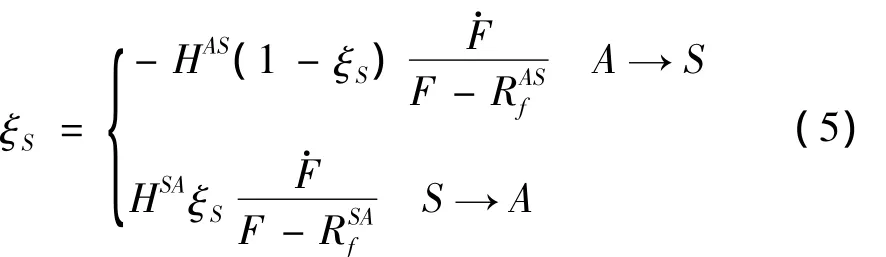
其中:

增量应力应变公式为:

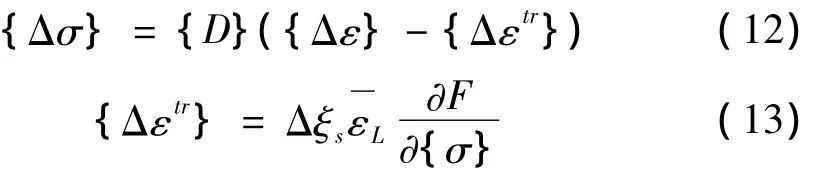
其中:［D］为应力应变矩阵，Δεtr为应变增量，εL为材料参数。

该模型将形状记忆合金的超弹性模型简化为理想的多段线性模型，虽然不够精确，但便于应用，并能够满足工程中分析的需要。

1.2 形状记忆合金的力学性能试验

本次试验选用西安赛特金属材料开发有限公司生产的组分为Ti－50.8at%Ni的形状记忆合金丝。SMA丝的最大回复应变为7%，最大回复应力为550 MPa。试件有效长度为150 mm，直径为1.0 mm。拉伸试验装置为微机控制电子万能试验机，采用50 mm标距的引伸仪测量位移，试验时首先在室温下进行拉伸、卸载循环试验，使材料的超弹性性能稳定，然后开始加载、卸载，绘制应力－应变曲线。试验装置及试件拉伸现场如图1所示，将试验所得的形状记忆合金的应力应变曲线等效拟合后得到的应力应变曲线如图2所示，拟合参数取值如表1所示。

图1 拉伸试验现场Fig.1 Tensile test site

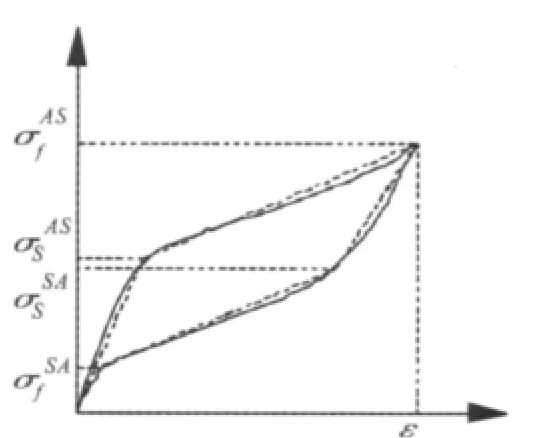
图2 等效线性化的SMA应力应变曲线Fig.2 Equivalent linear stress-strain curves

表1 拟合曲线参数的取值Tab.1 The parameters of fitting curve

2 消能减震装置的工作原理

本文所提出的消能减震装置主要用于减轻框架结构的底层柱子在地震作用下的破坏，由于地震作用的不确定性和结构设计时有些因素未能充分考虑(比如设计时未考虑楼板对梁的加强作用等)，导致很多情况下在柱端产生塑性铰。特别是框架结构底层柱，由于框架结构以剪切型变形为主，致使底层柱承受的倾覆力矩很大，导致柱底的弯矩很大，所以更容易在此形成塑性铰。

根据框架结构的变形特点，即在水平地震作用下，结构柱上一般都有反弯点，反弯点的位置与很多因素有关，但总可以近似的求出反弯点的高度，目前比较成熟的方法有D值法，而反弯点法是对D值法的一种简化近似方法。反弯点法近似认为结构的底层柱反弯点在柱子高度的2/3处，在其他层反弯点在柱子高度的1/2处。

本文正是根据一般框架柱中存在反弯点的变形特点，提出在底层柱反弯点的下方位置附近设置一个锚固装置，通过这一锚固装置，把柱子和形状记忆合金索连接起来，形状记忆合金索的下端垂直锚固在地下。在地震作用时，柱子要发生反复的弯曲变形，但反弯点的下方主要发生单向弯曲变形，这样柱子一边的形状记忆合金索受拉，而柱子另一边的形状记忆合金索处于卸载状态，通过拉索的超弹性反复变形实现了耗散地震能量的作用。具体安装时，可以等主体结构施工完成后安装形状记忆合金索，形状记忆合金索应张拉至其最大应变的一半左右，这样在加载和卸载时都能实现耗能作用。

消能减震装置安装的设计构思如图3所示，在底层柱的反弯点下方位置附近加设锚固装置，锚固装置可以由厚钢板和斜撑杆组成，钢板的作用主要是锚固拉索，斜撑杆的作用是固定钢板，保证钢板和框架柱变形协调。形状记忆合金索的上端固定在锚固装置上，下端锚固在地下。

形状记忆合金索由两段组成，一段为高强钢绞线、高强钢丝绳或钢丝束，另一段为形状记忆合金丝束部分。由于所采用的形状记忆合金的弹性模量较小，所以变形主要集中在形状记忆合金部分。在设计时，要保证锚固板的足够刚性，使其不要发生大的变形，这可以通过加大钢板的厚度和撑杆的刚度来实现。

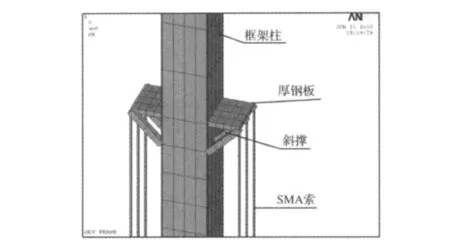
图3 新型抗震柱细部构造设计示意图Fig.3 Design detail of new seismic column

3 有限元分析模型

为了对本文所提出的设想进行验证，设计了2个单层单跨的钢管混凝土框架，一个是普通的钢管混凝土框架，另一个是设置了形状记忆合金索的新型钢管混凝土框架。应用ANSYS有限元程序对两个框架分别进行水平推覆数值计算和低周反复荷载计算来验证本文所提出的设想的可行性。有限元分析中，钢管和钢梁采用Q235钢，形状记忆合金索的等效直径为10 mm，最大可恢复应变为7%。为了建模方便根据抗弯刚度等效原则将工字型钢梁截面等效为矩形钢管截面。钢管混凝土框架结构的设计参数如表2所示。

表2 钢管混凝土框架结构的设计参数Tab.2 Design parameters of concrete-filled steel tubular frame structure

本算例中，形状记忆合金索上端通过锚板锚固在距离柱底2/3的位置处，锚板的挑出长度为20 cm。一般来讲，锚板的挑出长度即形状记忆合金索距柱子的合适距离可取20 cm～150 cm，形状记忆合金索距离柱子越远，则形状记忆合金索的伸缩变形越大，耗能效果越好，具体的合适距离可综合考虑需要达到的耗能效果和不影响实际使用的功能决定。在建模时，混凝土采用solid65单元，其单轴受压本构关系选用文献［14］所提出的本构关系，图4所示为混凝土的单轴受压应力－应变曲线。

钢管和钢梁选用solid45单元，本构关系为理想弹塑性，考虑应力强化段;锚板选用shell181单元，斜撑选用beam188单元模拟，形状记忆合金索采用solid185单元，这个单元在ANSYS中专门用来模拟SMA的性能。在有限元模型中，形状记忆合金计算取用的参数如表1所示。图5是新型框架的有限元模型。锚板处的节点详图可见图3。

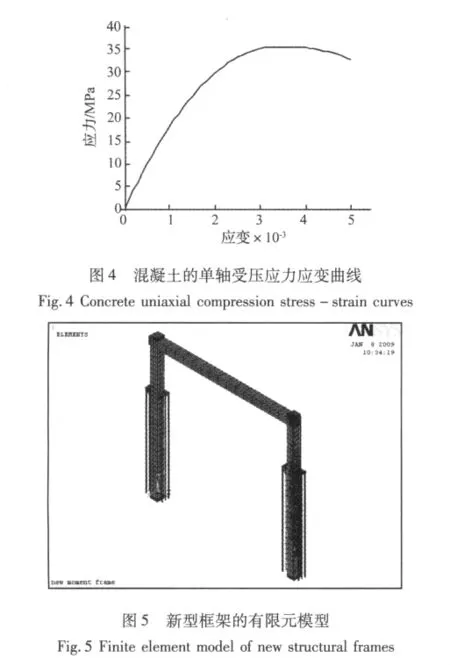
4 静力弹塑性分析

静力弹塑性分析可以较好的分析结构和构件的非线性变形性能，因此为了考察形状记忆合金索对框架承载力和延性的影响，本文对两种不同类型的框架进行了静力弹塑性推覆分析。

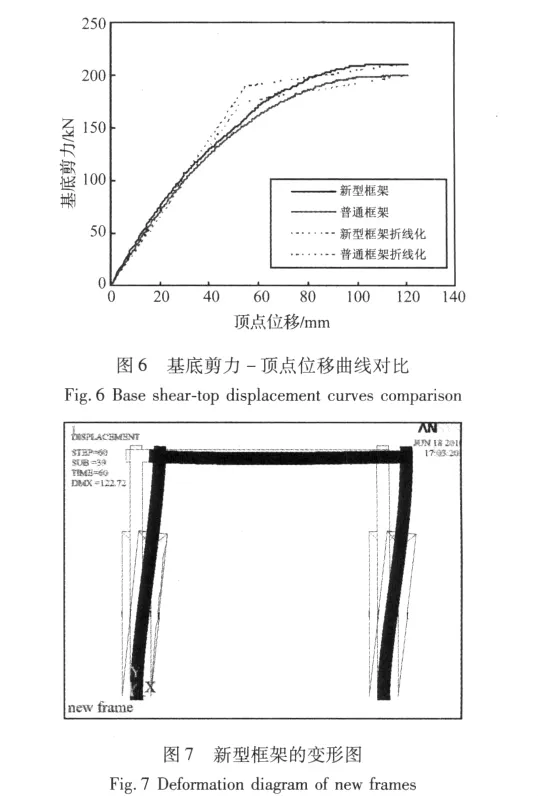
加载的过程为对普通钢管混凝土框架，先加竖向力荷载，直到框架柱的实际轴压比达到0.4，然后施加水平位移荷载;对设置了形状记忆合金索的新型钢管混凝土框架，先对框架施加竖向荷载，直到框架柱的实际轴压比达到0.4，然后对形状记忆合金索施加预应力，直到其应变达到可恢复应变的一半左右，即3.5%，最后施加水平位移荷载。两个框架顶点的水平位移都推到120 mm，层间位移角达到1/50。图6为静力推覆计算得到的结构基底剪力－顶点位移曲线。图7为新型框架的顶点推覆位移达到120 mm后的变形图。

基于FEMA273建议的折线化方法［15］，得到普通框架的屈服剪力和极限承载力分别为175 kN和200 kN，新型框架的屈服剪力和极限承载力分别为190 kN和212 kN，新型框架的屈服剪力提高了8.6%，极限承载力提高了6%，屈服位移也大于普通框架。普通框架的初始刚度为 3.3 kN/mm，屈服后的刚度是 0.486 kN/mm，刚度下降为初始刚度的14.7%;新型框架的初始刚度为 3.465 kN/mm，屈服后的刚度是 0.465 kN/mm，刚度下降为初始刚度的13.4%。所以新型框架的刚度退化速度和普通框架差不多，新型框架的承载力更高一些，可以抵抗更大的侧向水平荷载，但总的来说加设形状记忆合金索后对框架的承载力提高不明显。

5 低周反复分析

低周反复加载分析可以考察结构和构件的滞回耗能能力，因此分别对加设形状记忆合金索的新型框架和普通框架进行了低周反复加载计算。加载方式为先加竖向荷载并保持不变，然后施加水平位移荷载，采用来回往复变幅加载，每次位移增加5 mm后，来回往复循环一次，直到结构顶部的最大位移达到80 mm后停止加载，一共进行了16次循环加载，此时结构的层间位移角达到1/73。

5.1 结构滞回耗能能力

塑性滞回耗能能力是衡量结构抗震性能的重要指标，其数值越大，表明结构吸收地震能量的能力越强，结构抗倒塌能力越大。在反复循环荷载作用下，滞回环所包围的面积表示荷载反复交变一周时构件所吸收的能量。结构的耗能能力一般用两个指标控制，一个是衡量结构在某位移状态下循环一次所耗散的能量大小，这个指标可以用等效粘滞阻尼系数表示;另一个指标是衡量结构在整个位移过程中所耗散的能量大小，这个指标反映了结构的累积塑性耗能能力，可以用总的粘滞阻尼系数表示，也可以直接用总的塑性耗能表示。

图8所示为设置形状记忆合金索的新型框架与普通框架的滞回耗能曲线比较。由图8可见，设置了形状记忆合金索的新型框架的滞回环比普通框架更加饱满。在承载力极限荷载时，新型框架的等效粘滞阻尼系数是0.115，普通框架的等效粘滞阻尼系数是0.097，新型框架的等效粘滞阻尼系数是普通框架的1.2倍;通过对滞回曲线积分求得新型框架在16次循环中总的塑性耗能为53 187 kN·mm，普通框架总的塑性耗能为37 621 kN·mm，新型框架的耗能能力提高了41.4%，因此新型框架可以在地震中耗散更多地震能量，抗倒塌能力更强。

图8 滞回耗能曲线比较Fig.8 Hysteretic energy curves comparison

5.2 形状记忆合金索滞回耗能反应

为了使形状记忆合金索在拉压状态下都能够实现耗能，避免拉索的受压松弛，并且使得在整个循环变形过程中达到最大的耗能效果，本文在竖向荷载加载后，水平位移荷载加载前，对形状记忆合金索施加初始预应力，使其初始预应变达到形状记忆合金索最大可恢复应变的一半左右。由前述形状记忆合金材性试验所测得的其最大可恢复应变为7%，故其初始预应变加到3.5%左右。在ANSYS时间历程后处理器提取了形状记忆合金索的节点的应力－应变曲线，如图9所示，在整个低周反复加载过程中，形状记忆合金索始终处于受拉状态，其滞回环相当饱满，能够起到很好的耗能效果。ANSYS有限元分析得到的形状记忆合金的滞回环与实测的形状记忆合金的应力－应变曲线的形状基本一致，这表明了有限元程序里形状记忆合金的本构模型是可以很好地模拟形状记忆合金的性质。

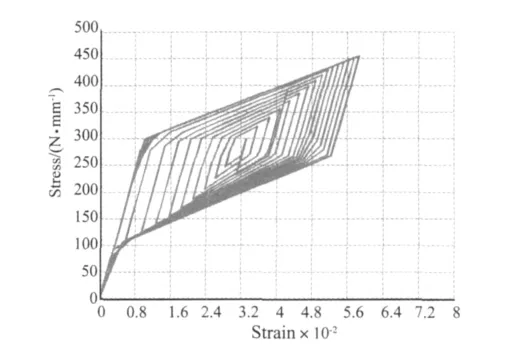
图9 SMA滞回耗能曲线Fig.9 SMA Hysteretic energy curves

6 对比分析比较

目前，已有的一种形状记忆合金索的设置方法为把拉索锚固在框架结构的对角位置处，因为对角位置的相对变形较大，研究表明该种设置方法耗能效果较好，但此种方法的不足之处是可能会影响结构的正常使用功能，因为对角锚固则意味着此处较难开设门洞，但本文提出的在反弯点下方处锚固就可以满足开设门洞的要求。

为了比较这两种锚固方式的耗能效果，建立了两个有限元模型，如图10和图11所示。

两个模型的框架相同，均为工字型钢框架，轴压比为0.4，都设置直径为10 mm的形状记忆合金索。反弯点设置的形状记忆合金索距离柱子的距离为100 cm。对这两个新型框架和普通的工字型钢框架做低周反复加载计算，最大位移推到120 mm，层间位移角达到1/50。计算表明，普通框架、反弯点设置SMA索框架、对角设置SMA索框架的基底最大剪力分别为291 kN、290 kN、301 kN。图12为三个框架的滞回曲线。

由于框架均为钢框架，所以三个框架的滞回曲线都很饱满，在24个循环中，普通框架耗能为520 000 kN·mm，对角设置 SMA索的框架耗能为562 204 kN·mm，反弯点下方设置 SMA索的框架耗能为538 301 kN·mm，对角设置SMA索的框架耗能能力提高了8%，反弯点下方设置SMA索的框架耗能能力提高了3.5%。尽管耗能能力提高的不多，但可以设置多根SMA索来增大耗能能力。总体来讲，对角设置SMA索的框架耗能效果最好，反弯点设置SMA索的框架次之，普通钢框架最差。因此，在实际工程中采用哪种设置方式，可以综合考虑框架处设置行人门洞否，如若设置，则可以采用反弯点处设置SMA索的方式;否则，采用设置对角SMA索的耗能效果更好。

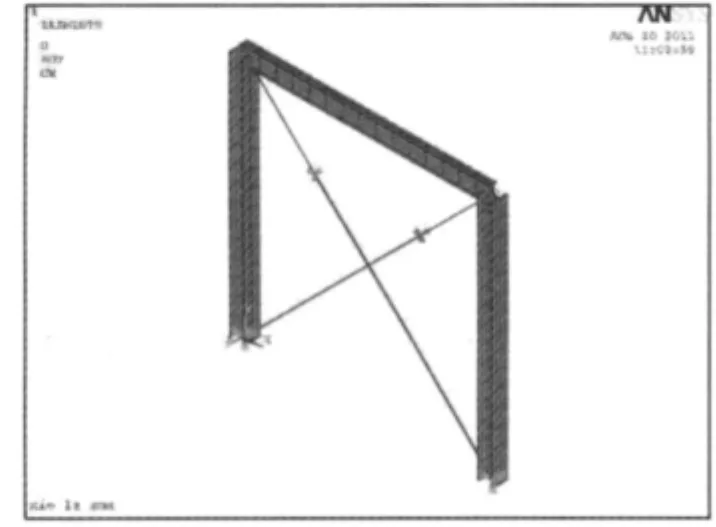
图10 对角锚固的有限元模型Fig.10 Finite element model of diagonal anchor

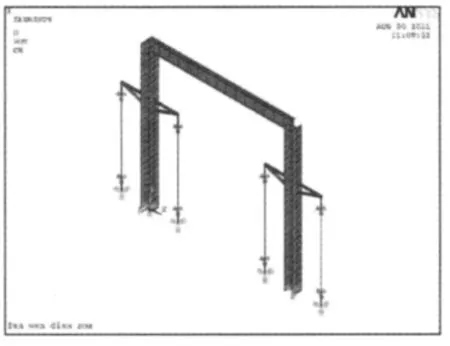
图11 反弯点锚固的有限元模型Fig.11 Finite element model of inflection point anchor

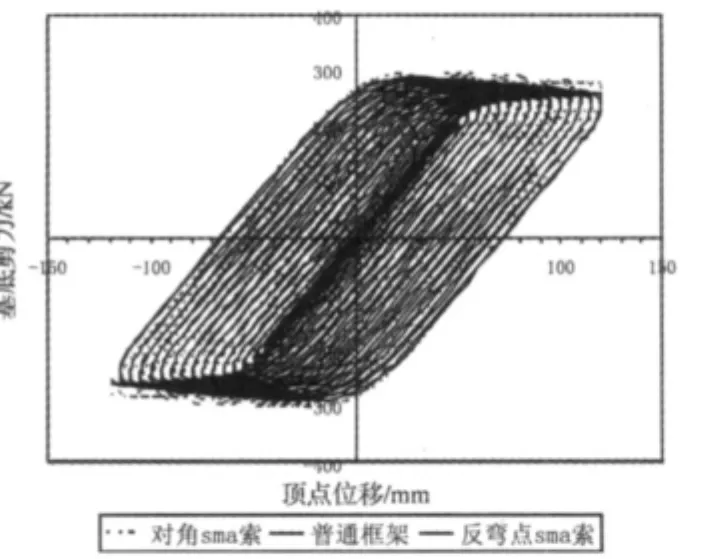
图12 滞回耗能曲线比较Fig.12 Hysteretic energy curves comparison

7 结论

本文首先通过材性试验研究了形状记忆合金丝材的超弹性变形性能，证明了其可恢复应变大，滞回环比较饱满，然后详细解释介绍了其超弹性本构模型，并根据框架结构的变形特点提出了一种基于形状记忆合金的消能减震装置，阐述了其工作原理，并通过静力弹塑性推覆分析和低周反复弹塑性分析得出以下初步结论:

(1)本文提出的基于形状记忆合金的消能减震装置具有自复位能力，并且构造简单。震后形状记忆合金索可以恢复到初始状态，残余变形小。

(2)材性试验表明，形状记忆合金的滞回环比较饱满，超弹性变形性能好，在实际应用时可以将其等效为多线性模型。

(3)静力弹塑性推覆分析表明，该消能减震装置可以使结构屈服承载力和极限承载力有所提高。

(4)低周反复分析表明，设置消能减震装置的框架相比普通框架，其滞回环更加饱满，其累积滞回耗能能力提高约41.4%，其极限承载力对应的等效粘滞阻尼系数也提高了约20%，在整个过程中形状记忆合金索的滞回环饱满，表明该消能减震装置可以显著地提高结构的耗能能力。

(5)通过对对角设置SMA索的框架与反弯点下方设置SMA索的框架的比较表明，对角设置SMA索的框架耗能效果更好，但反弯点处设置SMA索的框架可以满足开设行人门洞的要求，具体采用哪种设置方式，可以综合考虑决定。

［1］吕西林.复杂高层建筑结构抗震理论与应用［M］.北京:科学出版社，2007.

［2］薛素铎，董军辉，卞晓芳，等.一种新型形状记忆合金阻尼器［J］.建筑结构学报，2005，26(3):45－50.XUE Su-duo，DONGJun-hui，BIAN Xiao-feng，et al.A new type of shape memory alloy damper［J］.Journal of Building Structures，2005，26(3):45－50(in Chinese)

［3］薛素铎，石光磊，庄 鹏.SMA复合摩擦阻尼器性能的试验研究［J］.地震工程与工程振动，2007，27(2):145－151.XUE Su-duo，SHI Guang-lei，ZHUANG Peng.Performance testing of SMA incorporated friction dampers［J］.Earthquake Engineering and Engineering Vibration，2007，27(2):145－151(in Chinese).

［4］薛素铎，庄鹏，李彬双.SMA－橡胶支座的力学性能试验研究［J］.世界地震工程，2005，21(4):10－15.XUE Su-duo，ZHUANG Peng，LI Bin-shuang.Experimental study on mechanical behavior of SMA-rubber bearing［J］.World Earthquake Engineering，2005，21(4):10－15(in Chinese).

［5］王社良.形状记忆合金在结构控制中的应用［M］.西安:陕西科学技术出版社，2000.

［6］欧进萍.结构振动控制－主动、半主动和智能控制［M］.北京:科学出版社，2003.

［7］Song G，Ma N，Li H N.Applications of shape memory alloys in civil structures［J］.Engineering Structures，2006:1266－1274.

［8］ Roh J H，Lee I，Han J H.Damping characteristics of SMA films and their application for passive vibration isolation［J］.International Journal of Applied Electromagnetics and Mechanics，2008，27(3):225－241.

［9］Dolce M，Cardone D，Marnetto R.Implementation and testing of passive control devices based on shape memory alloys［J］.Earthquake Engng Struct.Dyn.2000:945 －968.

［10］ Baz A，Iman K，Mccoy J，et al.Active vibration control of flexible beams using shape memory actuator［J］.Journal of Sound and Vibration，1990，140(3):437 －456.

［11］ Wilde K，Gardoni P，Fujino Y.Base isolation with shape memory alloy device for elevated highway bridges［J］.Engineering Structure，2000，22:222 －229.

［12］Dolce M，Cardone D.Mechanical behaviour of Shape Memory Alloys for seismic applications，Austenite NiTi wires subjected to tension［J］.International Journal of Mechanical Sciences，2001，43:2657 －2677.

［13］ ANSYS，Inc.Theory Reference.ANSYSRelease 9.0，2004.

［14］韩林海.钢管混凝土结构理论与实践(第二版)［M］.北京:科学出版社，2007.

［15］ Building Seismic Safety Council.NEHRP Guidelines for the Seismic Rehabilitation of Buildings［S］.FEMA － 273，Federal Emergency Management Agency，Washington DC，1997.