有阻尼负载时圆柱壳的声传递特性分析

姚熊亮，王献忠，孙龙泉

在国防和工业领域，特别是在航空、船舶和化工行业，在结构表面敷设阻尼材料这种方法在抑制振动与声辐射方面得到广泛应用。作为从这些行业中的典型工程结构中抽象出来的理论模型——带有阻尼负载的圆柱壳结构，它的声传递特性问题实质上是一个流－固耦合系统的声传递问题，一直以来都是国内外研究的热点。Kagawa等［1］首先针对圆柱薄壳一面敷设阻尼材料的情况，进行对称和非对称模态分析，Markus［2－3］应用经典薄壳理论研究了有限长圆柱壳的阻尼特性，分别讨论了阻尼负载在壳体外表面、内表面、内外表面的情况。Iyer［4］用模态分析法和壳体理论研究了圆柱壳在具有与正则模态相同分布的线激励作用下的声振响应。Zhang［5－6］采用复模量形式计及壳体和粘弹性阻尼材料的损耗因子，用迁移矩阵法研究了周期粘弹性复合圆柱壳的波传播和功率流。这些研究侧重在圆柱壳声传递机理及表面阻尼处理方法上，而对如声波入射角度、结构参数等因素对声传递的影响研究很少涉及。然而结构声传递特性是噪声控制和结构声学设计的重要参考依据，因此开展有阻尼负载的圆柱壳的声传递特性研究具有广泛且重要的工程指导意义。Koval［7］开展了斜入射平面波入射到各向异性圆柱壳上的声波传递特性研究。Daneshjou等［8］主要针对各向异性复合材料圆柱壳的声波传递特性进行研究，但是其中给出的声振耦合方程忽略了部分高阶项。本文采用文献［7］中对复合壳体的描述方法，并对文献［8］中的声振耦合方程进行补充，给出修正后的复合壳体的运动微分方程。在此基础上，本文主要对浸没在匀速流动的流体介质中的阻尼负载圆柱壳的声传递特性进行研究，着重讨论分析了声波入射角度、阻尼厚度、壳体厚度、壳体半径等对声传递损失的影响，所得结论对指导结构声学设计具有重要意义。

1 理论分析

1.1 复合壳体运动方程

考虑有阻尼负载的圆柱壳，假设圆柱壳为无限长薄壳，外界环境为均匀流动的理想流体，如图1所示。浸没在流体中无限长有阻尼负载的圆柱壳振动方程可由板壳理论［9］中壳体的平衡微分方程推导得到。本文考虑两弹性层胶合的复合壳系统，其中内部弹性层为弹性圆柱壳，厚度为h1，弹性模量为E*1，取E*1=E1，泊松比为μ1;外部粘弹性层为阻尼负载层，厚度为h2，泊松比为μ2，弹性模量为复模量E*2=E2(1+iη)，其中η为粘弹性材料的损耗因子。

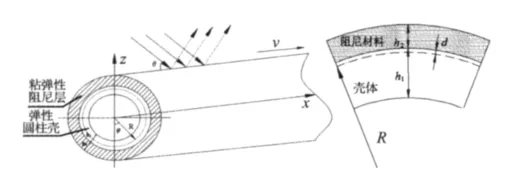
图1 有阻尼负载圆柱壳的结构模型示意图Fig.1 Computational model of cylindrical shell with damping layer load

基于板壳的Kirchhoff假设，复合壳的平衡微分方程［3］可表示为:

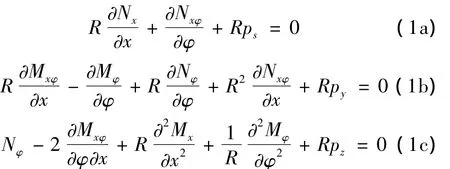
其中:R 为复合壳体的平均半径，Nφ、Nx、Nxφ、Mxφ、Mx、Mφ分别表示由壳体变形所引起沿 x，y，z三个方向

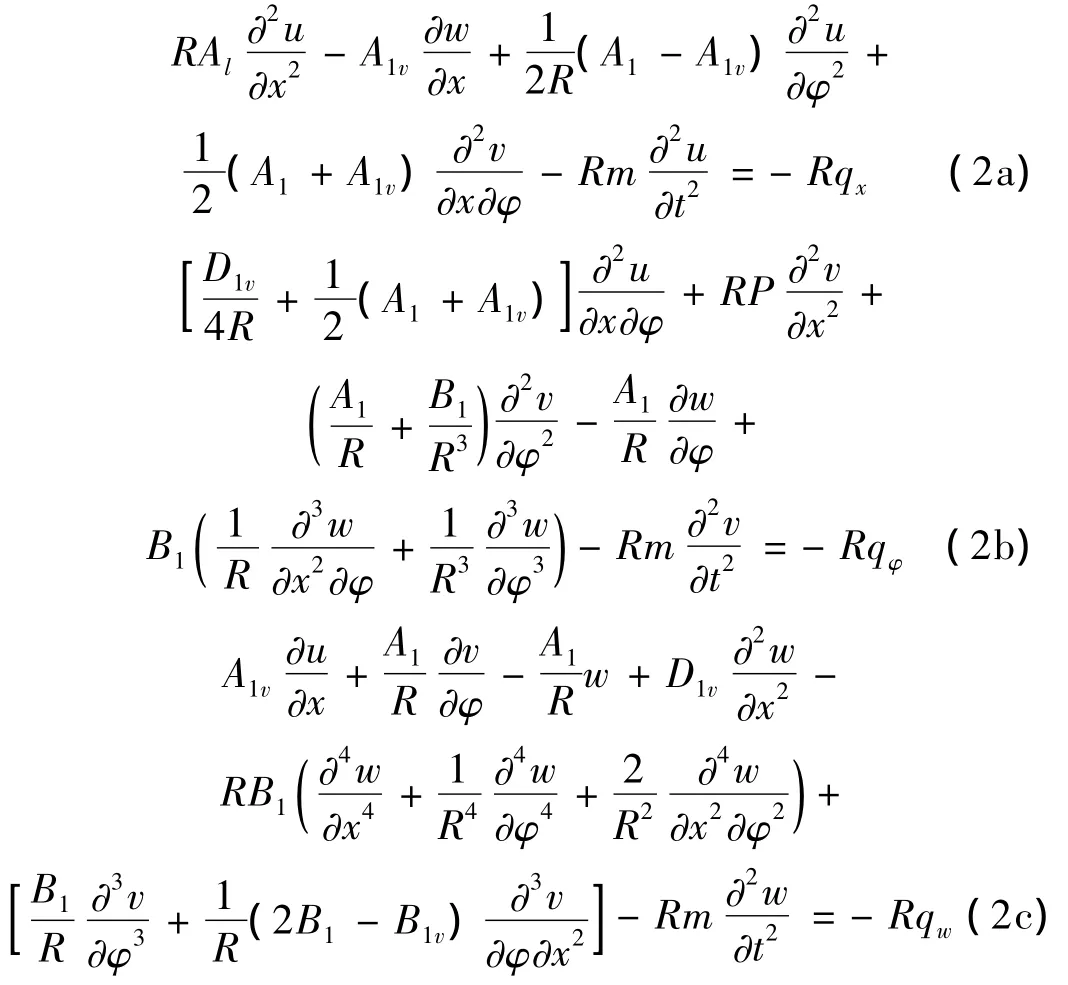
式中:x，φ和r分别表示壳体的轴向、周向和径向自变量，u，v和w分别为壳体的轴向、周向和径向位移。m代表有阻尼负载圆柱壳单位面积的质量。A1、A1v、B1、B1v、D1v、p表达式见附录。假设与壳体轴向波数k1x有关的壳壁位移的简正波模式为:

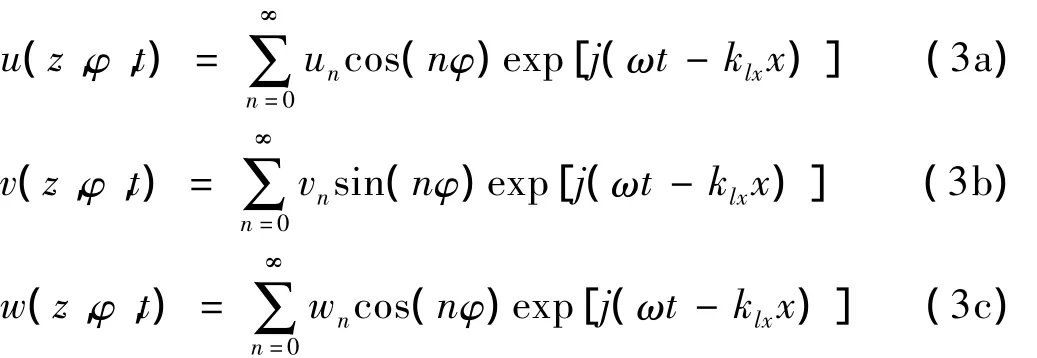
将方程(3a)、(3b)、(3c)代入方程(2a)、(2b)、(2c)中可得:

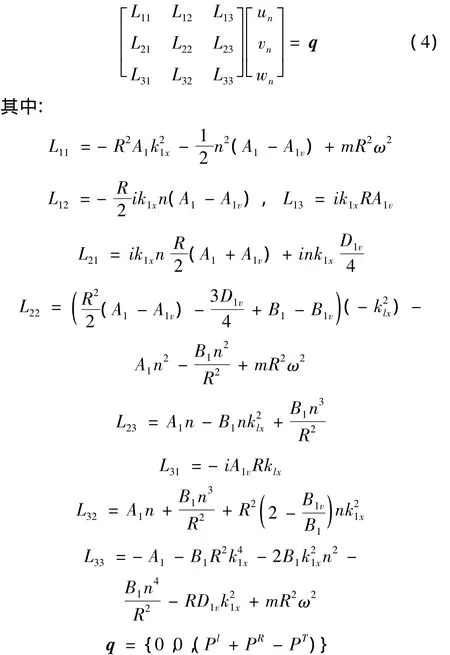
1.2 流体介质中的声场

声波在均匀流动流场中传播，因而声压P必须满足流场中的波动方程，由此可得:

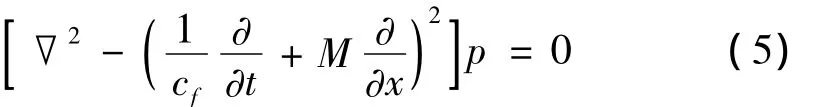
其中:M为Mach数，cf为流体中的波速。

柱坐标系下的简谐入射波Pl可以表示为［10］:

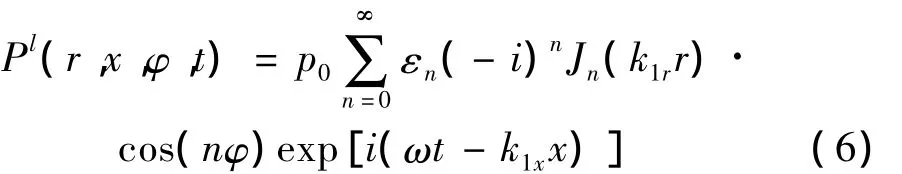
式中:εn为Neumann因子，即:

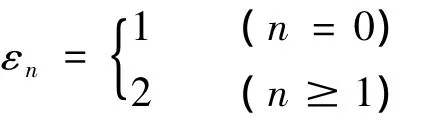
k1= ω/c1(1+M cosθ)，k1x=k1cosθ，k1r=k1sinθ，M 代表马赫数，θ代表入射角度。

依据Hankel函数［10］性质，有阻尼负载圆柱壳体上的反射波和透射波可分别表示为:

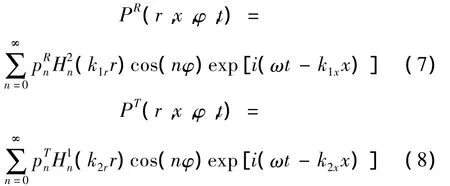
1.3 边界条件

在流体与壳体的接触面上，外(内)部流体的径向位移必须等于有阻尼负载圆柱壳体的径向位移，即:

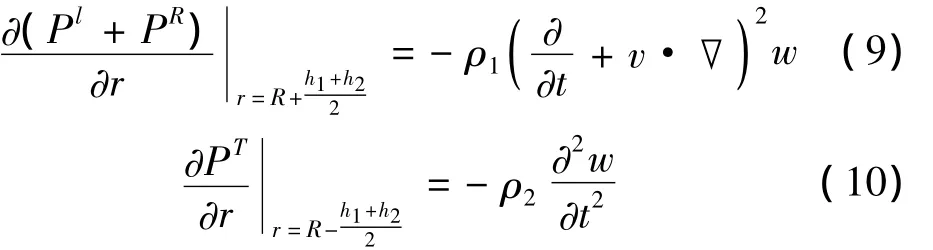
1.4 声波的传递损失

将方程式(3c)、(6)、(7)、(8)代入到方程(9)、(10)中可得:

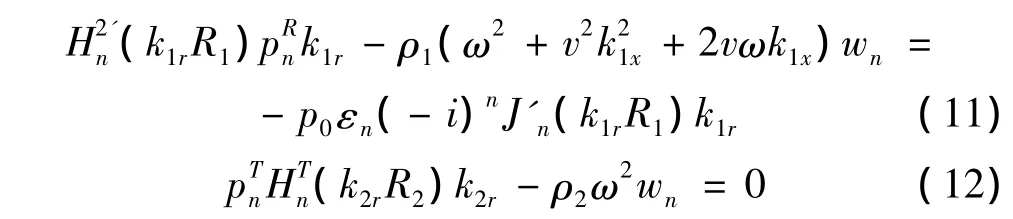
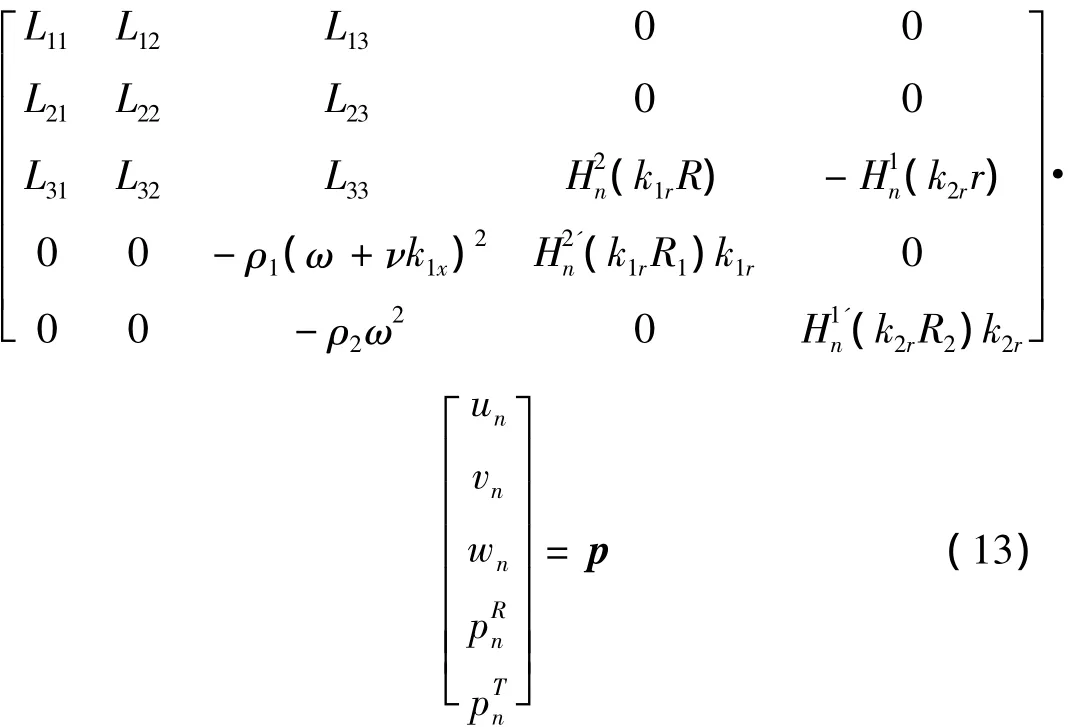
其中:p={0，0，－p0εn(－i)nJn(k1rR)，－p0εn(－i)nJ'n(k1rR1)k1r，0}，因此所有未知数项均可由激励输入项p0表示。

声波在有阻尼负载圆柱壳中的传递损失［7］可以定义为自由阻尼负载外界流体中的入射声功率与透射到壳体内部流体介质中透射声功率之比:

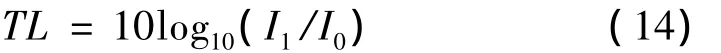
其中:入射声功率及透射声功率为:

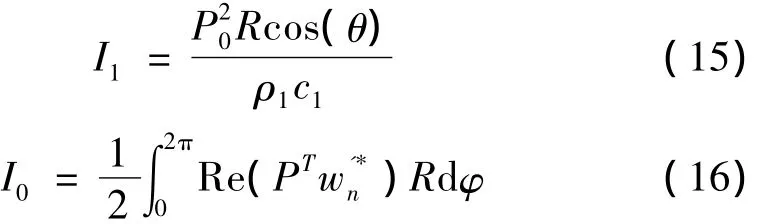
将式(15)、式(16)代入到式(14)中可以得到:

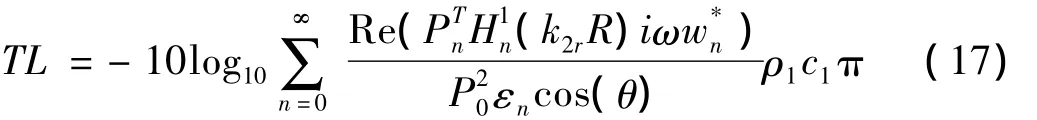
2 数值结果

本文以浸没在水中的有阻尼负载圆柱壳为例，计算了声波在其中的传递特性。计算中取:内层弹性材料取钢板，弹性模量 E=2.1e11 N/m2，泊松比 μ =0.3，密度ρ=7 800 kg/m3，厚度h1=0.001 m;外层粘弹性阻尼材料，弹性模量E=1e8 N/m2，泊松比μ=0.5，密度ρ=1 100 kg/m3，厚度 h1=0.002 m，损耗因子 η =0.4，壳体平均半径R=1 m。水的密度ρ=1 000 kg/m3，水中声速c=1 500 m/s。

为了验证本文计算方法的有效性，分别采用本文方法及文献［7］中方法对有阻尼负载圆柱壳时的声传递损失进行计算，图2为本文计算方法与文献中计算结果的对比曲线。从图2中可以发现，采用本文方法计算结果与文献［7］中结果吻合较好，证明本文方法的有效性。但是在低频时，两者的计算结果稍有差异，这是因为文献［7］中未考虑轴向和周向的惯性项。

同时从图2中可以发现，圆柱壳结构的传递损失与结构的固有频率和激励频率密切相关。当激励频率与其固有频率相等时，结构的声传递损失急剧下降，出现声传递损失的“失效频率点”，图中计算结构的固有频率为67 Hz。同时传递损失曲线具有明显的环频率点fr和吻合频率点fc，从(0－fr)频带内，声波的传递受到刚度调整，(fr－fc)频带内，声波的传递受到质量控制，(f＞fc)则位于吻合控制区，这与文献［7］的理论分析相符，从而进一步验证了本文计算方法的合理性和正确性。

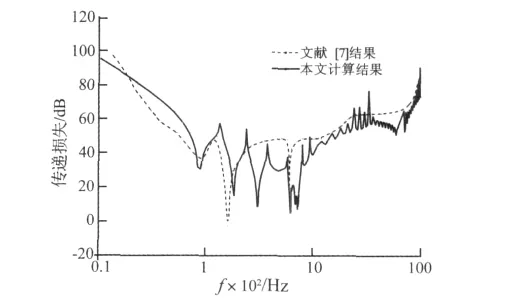
图2 声传递损失随频率的变化曲线Fig.2 Curve of sound transmission loss

3 声传递特性

为了研究复合圆柱壳声传递特性，分别计算分析了不同声波入射角度、不同阻尼层厚度、壳体厚度和壳体半径对声传递损失的影响。

图3 给出了入射角度分别为 30°、45°、60°时声波的传递损失情况。从图中可以发现，随着入射角度的增加，在(0－fr)、(f＞fc)频带内的传递损失曲线也随之降低，而在(fr－fc)频带内，变化趋势比较复杂，交错在一起。整体来说，随着声波入射角度的增加，圆柱壳声传递损失随之减少。

图4给出了阻尼负载厚度h2分别为2 mm、5 mm和10 mm时声波的传递损失。从图中可以发现，随着厚度的增加，在低频段有一个区域，随着阻尼负载厚度的增加其对应的传递损失反而急剧下降，这个区域是阻尼负载的失效区，阻尼负载越厚降噪失效区的频率范围越宽，数值越小。同时阻尼层厚度的变化会改变传递损失的共振频率，并且整体上声传递损失随着阻尼负载厚度的增加而增加。

图5是阻尼负载覆盖在不同厚度(分别为1 mm、2 mm、10 mm)圆柱壳壳体上的传递损失。从图中可以很明显看出，阻尼负载覆盖在厚壳体钢板上的效果比较好，由分析可知壳体钢板增厚，其对应的阻抗也随之增加，与阻尼负载的差别明显。同时从另一方面考虑也可知，壳体钢板厚度的增加会使阻尼负载圆柱壳的总刚度增加，进而导致传递损失增加。

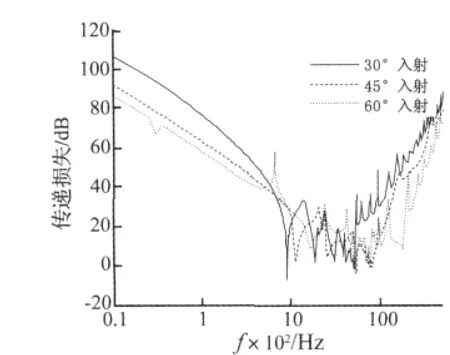
图3 入射声波角度对声波传递损失的影响曲线Fig.3 Curve of sound transmission loss with different incident angle

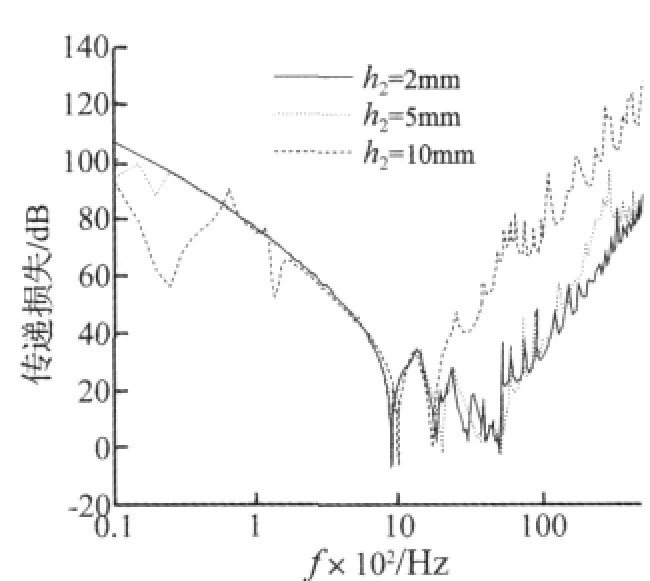
图4 阻尼负载厚度对声传递损失的影响曲线Fig.4 Curve of sound transmission loss with different damping layer thickness

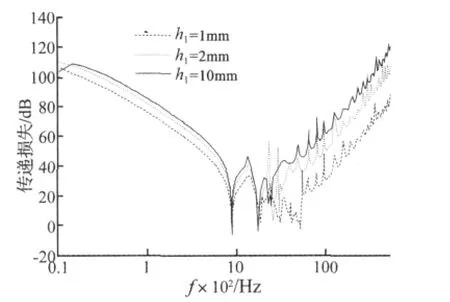
图5 壳体厚度对声传递损失的影响曲线Fig.5 Curve of sound transmission loss with different shell thickness

图6 是圆柱壳壳体平均半径(分别为0.1 m、1 m、10 m)对声波传递损失的情形。从图中可以很明显看出，在低频段，半径越小，其传递损失越大，这是由于当半径变小时，同样的壳体厚度，其圆柱壳壳体总刚度变大，进而导致传递损失增加。当处于中高频带，这时半径越大其对应的传递损失反而越大。但其声波传递损失不会随着频率的增加而无限增加，由于波长变短，传递损失会趋于稳定。

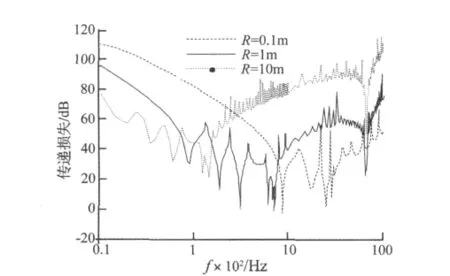
图6 壳体平均半径对声传递损失的影响曲线Fig.6 Curve of sound transmission loss with different shell radius

由图5和图6可以看出，圆柱壳的固有频率可能会导致隔声失效，因此提高圆柱壳的声传递特性，就要避免共振。改变板厚和壳体半径后，结构固有频率的改变会使得圆柱壳声传递损失曲线的隔声失效频率发生改变。

4 结论

(1)当入射声波频率与圆柱壳固有频率相等时，其传递损失会急剧下降，出现“失效频率点”;

(2)入射声波角度的增加，整个频带内的声传递损失呈下降趋势;

(3)一般情况下，随阻尼层厚度的增加，声传递损失随之增加，但是在低于环频率的频段内存在一个声传递损失的失效区域。随着阻尼负载厚度增加，传递损失不升反降，阻尼负载对噪声起放大作用。因此，在工程设计中，应该注意避开这一区域，以免起到反效果;

(4)随圆柱壳壳体平均半径的增加，低频段声传递损失随之减小，而高频段随之增加。

［1］Kagawa Y，Krokstad A.On the damping of cylindrical shells coated with viscoelastic materials［M］.ASMEPublication 69-vibr.9，1976:1 －9.

［2］Markus S.Damping properties of layered cylindrical shells vibration in axially symmetric modes［J］.J.Sound Vib，1976，48(4):511－524.

［3］Markus S.Refined theory of damped axisymmetric vibrations of double-layered cylindrical shells［J］.J.Mech.Eng.Sci.，1979，21:33 －37.

［4］Iyer K M.Modal response of a circular cylindrical shell with damping layers［D］.The Ohio State University，Ph.D.Thesis，1980.

［5］Zhang X M.Parametric studies of coupled vibration of cylindrical pipes conveying fluid with wave propagation approach［J］.Computer and Structure，2002，80:287－295.

［6］张小铭，张维衡.周期粘弹性复合壳的功率流［J］.振动工程学报，1993，6(1):1－9.

［7］Koval L R.On sound transmission into a thin cylindrical shell under“flight conditions”［J］ .J.Sound Vib.，1976，48(2):265－275.

［8］Daneshjou K，Nouri A，Talebitooti R.Sound transmission through laminated composite cylindrical shells using analytical model［J］.Archive of Applied Mechanics，2007，77:363－379.

［9］Timoshenko S，Woinowsky-Krieger S.板壳理论［M］.北京:科学出版社，1977.

［10］奚定平.贝赛尔函数［M］.北京:高等教育出版社，1998:118－120.

附录: