基于表面肌电信号高通滤波处理后对指屈肌肌力估算的研究

郭 峰

在体育运动中，对肌肉力量的研究是一个长久的课题，利用生物力学手段研究肌肉力量的一个不足就是不能够直接测量活体条件下某一块肌肉的力量。De Luca［8］指出，表面肌电信号经过整流和平滑以后，其幅值大小可以定性地反映某一个关节力矩或者力量的大小，但是想定量地反映出关节力量大小却很难。直接评价某一块肌肉力量最普遍的方法就是使用表面肌电（surface electromyography，sEMG）［5，15，22］。肌电图记录到的肌电信号实际是运动单位动作电位在肌纤维上传导到电极所在位置时在时间和空间上的叠加，是一种复合动作单位。肌电信号本质上包含着被激活运动单位的数目以及每一个运动单位发放的频率。肌纤维上产生动作电位后通过兴奋收缩耦联途径诱发肌纤维收缩，由于肌纤维收缩曲线的不应期短，在收缩曲线在收缩期可以叠加，进而使产生的肌力发生叠加。当动员的运动单位数目或者同步化程度增高时，叠加的复合运动单位幅值增高，肌电信号增强，募集收缩的肌纤维数目增多。因此，肌肉的收缩力会随着肌电幅值的增加而增强，两者之间是存在特别关系的，这可以通过一些方法根据肌电信号推测出相应的肌肉力量信息。但是，在进行估算前，需要对原始sEMG进行处理，处理过程主要涉及：1）对某一块肌肉的电信号进行差分放大；2）对信号进行带通滤波；3）全波整流；4）对肌电信号进行低通滤波，进而确定一个“线性包络”（linear envelope）。进行低通滤波的目的主要是想显现出肌肉对运动单位动作电位（motor unit action potentials，MUAPs）脉冲产生 的二阶 反应，同时，由低通滤波引起的相位延迟也能够反映出肌肉收缩过程中的电机械延迟现象［25］。对经过低通平滑处理后的信号进行标准化处理，即将信号表示为肌肉进行最大随意收缩（maximum voluntary contractions，MVCs）时肌电信号的百分比。实际上，对力量进行进一步精准地估算还需要知道肌肉横断面积、肌肉长度以及肌肉收缩和拉长的速度。除此之外，学者们已经发现sEMG幅值与力之间的非线性关系，并通过使用非线性标准化的方法将其校正［9，11，20］，进而进行定量分析。

目前，有很多文献表明，在对信号进行带通滤波时，一般首先需要对原始肌电信号进行高通滤波，截止频率一般为30Hz［2，1418］。带通滤波处理还应该包括低通滤波过程，低 通截 止 频 率 用 得 比 较 多 的 是 500Hz［1，6，8，23］，但 也 有 用250Hz［14］、300Hz［10］、450Hz［16］和490Hz［17］，采用这些截止频率的目的就是为了去除噪声并且保留真实的肌电信号。当然，在做这些处理时，是假设信号经过差分放大后频率成分不变，这样才会提高对肌肉力量估计的合理性。但也有一些证据暗示这种假设不准确。学者们发现，在长时间的等长收缩过程中sEMG幅值增加，但肌肉力量却没有增加［424］，这使得利用疲劳时的sEMG信号去预测力量受到质疑。在肌肉疲劳时sEMG的功率谱向左移，低频成分增加［310］。假设在肌肉力量不变时sEMG幅值一直增加，并且信号中增加的主要是低频成分，那么，在这小范围内变化的sEMG和力之间可能不存在关系。

用sEMG信号来表示肌肉对运动单位动作电位产生的二阶反应时，由于组织的滤波特性以及差分放大过程可能会引起基于sEMG对力量进行估算时发生的错误。同样，如果肌肉发生疲劳时sEMG的低频成分增加，这样，使用整个原始sEMG信号（20～500Hz）去评估肌肉力量是不准确的。

本研究目的是要确定20Hz以上不同高通截止频率对基于sEMG对指屈肌力量估计的影响，本研究假设，经过高通滤波处理后去除原始sEMG信号中大部分低频功率成分，可以显著地提高基于sEMG对力量进行估算的效果。

1 研究对象与方法

1.1 研究对象

本研究将受试者分成两组，受试者都来自体育学院体育教育学院的在校大学生，其中一组有9名健康成年男性（年龄：21.5±0.3岁，体重：70.1±1.2kg，身高：176.3±2.1cm，BMI＝24.5±2.5）；另外一组也由9名健康成年男性组成（年龄：20.2±0.5岁，体重：72.2±1.5kg，身高：174.2±3.5cm，BMI＝23.2±2.7）。两组在体重和BMI方面都没有统计学差异。

1.2 研究方法

1.2.1 实验仪器与材料

ME6000表面肌电仪、Ag／AgCl表面电极（小电极直径为0.8cm，两个记录电极距离为2cm；大电极直径为1.6 cm，电极距离为4cm）、电子拉力计、电脑。以上使用的实验仪器均来自沈阳体育学院国家体育总局重点实验室和电生理实验室。

1.2.2 数据采集

两组受试者的实验程序一样，首先，将两个表面记录电极置于右利手指屈肌肌腹的中线处，这样可以避免神经肌肉支配区域，参考电极置于肱骨的内侧髁。表面肌电信号采样频率为1 000Hz，50Hz共模抑制比例为115dB，增益为1 000，滤波范围20～500Hz。

受试者坐在电脑前，右手肘关节呈现90°，肘关节处于旋内旋外的中间位置，腕关节自然伸直，身体坐位时处于正常的解剖位置，肩关节自然下垂，处于正常解剖位置，手握电子握力计。实验前，让受试者熟悉实验过程，体验握力感觉，从而找到自己产生最大随意收缩的握距。令受试者指屈肌进行间断性的等长收缩，每名受试者收缩6次，在这6次收缩中包括2次快速收缩、2次快速最大随意收缩和2次相对较长时间收缩。

1.2.3 数据处理

对采集到的力值采用1阶Butterworth低通滤波，截止频率为30Hz，在实验采集到的数据中找到指屈肌肌力的最大值，并且将所有力值都相对最大力值进行标准化处理，表示为最大力值的百分比。采用一系列的过程对数据进行处理，包括：1）采用不同方法对原始肌电信号进行预处理；2）对整流后的信号进行不同低通截止频率滤波；3）对低通滤波后的信号进行不同的非线性标准化常数进行校正，最后评价sEMG与力之间的关系。具体步骤如下：1）选定1阶和6阶作为滤波阶数，这两个阶数最具代表性；2）对原始sEMG信号分别进行1阶和6阶低通滤波，截止频率为450Hz；3）对处理后的sEMG信号再分别进行1阶和6阶高通滤波，截止频率为20Hz；4）将上一步的sEMG信号进行全波整流；5）将整流后的sEMG信号再进行截止频率为1.0Hz的低通滤波（首先使用1阶Butterworth）；6）经过滤波整流后的sEMG信号再进行线性的标准化处理，即将滤波整流后的sEMG信号的每一个幅值表示为滤波整流后的sEMG信号最大幅值的百分比；7）对信号采用渐进性增大的非线性常数进行非线性标准化处理，非线性常数从0增加到50，每阶增加1，共51个常数，公式1［20］如下：

EMGlinear是指EMG相对最大值的线性标准化值，EMGnonlinear是指相对于最大值的非线性标准化值，C是定义的非线性标准化常数，这个非线性标准化常数可以保证肌电数据在0%～100%MVC之间［20］；8）将按照上述步骤处理后的sEMG信号与标准化力值信号进行比较，主要比较两者的RMS差值以及相关系数，对于RMS的差用RMS误差百分比表示，公式2［23］如下：

此处RMSdifference是指sEMG信号与力值信号RMS的差值，RMSforce是指力信号的RMS，ErrorRMS%是指sEMG信号与力值信号两者之间的差异，该值越大说明用sEMG信号估计力值效果越差。

在第5步中，将低通滤波截止频率分别设置为从1.0 Hz到4.0Hz，按每阶0.1Hz增加，共31个。这样，对于经过20Hz高通滤波后的原始肌电信号共有1 581种组合处理（51个非线性常数×31个低通截止频率），在这1 581个组合处理中，选定与力值RMS差值最小的，即sEMG信号与力值信号最相近的。实质上，整个处理过程从第3步开始，以不同的高通截止频率进行处理（从最初的20Hz到480Hz，每阶增加20Hz，共24个），一旦完成1阶滤波处理后，再进行6阶滤波处理，具体处理过程如图1所示，1阶Butterworth处理后，再选取6阶Butterworth滤波进行重复处理。

图1 本研究数据分析步骤流程图Figure 1. Flow Chart of Data Analysis Steps

在高通滤波处理过程中，需要记录的变量有：1）最佳的低通截止频率；2）最佳的非线性标准化常数；3）最小的ErrorRMS%；4）sEMG与力值最佳的相关系数；5）经过处理后的肌电信号整个功率谱。

文中不同的滤波方法以及RMS的计算通过MATLAB 7.1软件来完成。

1.2.4 统计学分析

本研究采用SPSS 12.0进行数据的统分析，采用2×2×24多因素方差分析，因变量为：1）ErrorRMS%；2）相关系数。独立变量为：1）电极尺寸大小，2个水平（大尺寸和小尺寸），为组间变量；2）高通滤波阶数，2个水平（1阶和6阶），为组内变量；3）高通截止频率共24个水平（20～480 Hz，每阶20Hz），为组内变量，显著水平为P＜0.05。目前，绝大部分的研究都是将20Hz高通滤波作为基于sEMG力值预测的标准，因此，将20Hz高通滤波与其他高通截止频率滤波时进行比较，采用配对t检验的方法进行比较。将在1阶和6阶每一个高通截止频率滤波处理后的信号与20Hz高通滤波相比。

2 结果

2.1 单一样本特征分析

图2是一名受试者一次快速收缩时，肌力与sEMG之间的关系，可见两者呈非线性变化关系。在该例实验中，肌电各项处理参数如下：1阶Butterworth高通滤波截止频率为440Hz，低通滤波截止频率为1.8Hz。

图3是同一名受试者6次不同收缩形式时基于指浅屈肌sEMG对肌力的估计，该图是在图2基础上经进一步非线性标准化处理得到的，最佳的非线性标准化参数为17，图3显示ErrorRMS%是如何计算的，0线以下的曲线部分为ErrorRMS%，即力值的RMS与表面肌电信号RMS的差值／力值RMS的绝对值。从图3可知，利用上述一系列处理方法对sEMG信号和力信号进行处理后，利用sEMG信号可以准确地评估力量大小。

图4是同一名受试者一次收缩时ErrorRMS%和相关系数变化特征（与图2是同一数据），该名受试者此次收缩时，sEMG信号值与力值之间的相关系数在0.84～0.94之间。

图2 本研究1名受试者指屈肌肌力与sEMG非线性关系示意图Figure 2. Non－linear Relationship Between Digital Flexors Force and sEMG for a Subject

图3 本研究1名受试者非线性标准化处理后sEMG与肌力之间关系曲线图Figure 3. Relationship Between sEMG and Force After Non－linear Normalization Process for the Same Subject

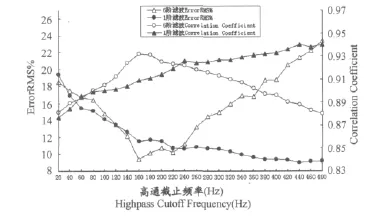
图4 本研究1名受试者sEMG经过1阶和6阶24个不同高通截止频率后ErrorRMS%与相关系数曲线图Figure 4. ErrorRMS%and Correlation Coefficients Resulting from Each of 24High－pass Cutoff Frequencies with 1st and 6th Order Filters Respectively for a Subject

2.2 ErrorRMS%

ErrorRMS%受高通截止频率（P＜0.01）和滤波阶数（P＜0.01）的影响，并且存在显著的高通截止频率与滤波阶数交互作用影响（P＜0.01）。电极大小对ErrorRMS%没有显著影响。对于1阶滤波器来说，标准20Hz高通滤波后的ErrorRMS%要显著高于其他所有高通截止频率（40～480 Hz）滤波后的ErrorRMS%（P＜0.01，图5）。

在图5中对于1阶滤波起来说，在18名受试者中有16名受试者的ErrorRMS%出现在440Hz时，平均最小值为9.1%±1.5%，相当于20Hz时 ErrorRMS%的51.7%，在460Hz以后ErrorRMS%开始稍稍升高。而对于6阶滤波来说，全部18名受试者的ErrorRMS%变化与1阶滤波相比较有一个明显的拐点，整体上表现为先减小后增大，而ErrorRMS%最小值出现在160Hz处，平均最小值为8.9%±1.8%，相当于20Hz时的45.6%。

2.3 相关系数

对于相关系数来说，高通截止频率有一个显著的主效应（P＜0.01）以及显著的高通截止频率和滤波阶数交互作用（P＜0.01），电极大小并没有显著影响相关系数。对于1阶滤波来说，相关系数与ErrorRMS%的变化相似，其他高通截止频率下的相关系数都要比20Hz高通滤波时相关系数大，最高相关系数时对应着440～480Hz（0.938～0.940）。对于6阶滤波来说，在40～460Hz范围内的相关系数都要大于20Hz时的相关系数，唯有480Hz时的相关系数小于20Hz时相关系数，最高相关系数也出现在160Hz处，平均为0.932±0.002。

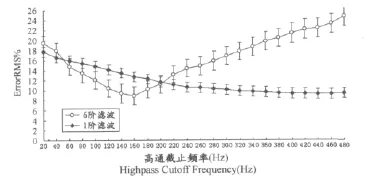
图5 本研究1阶和6阶不同高通截止频率下平均ErrorRMS%变化曲线图Figure 5. Average ErrorRMS%for Each High－pass Cutoff Frequency with 1st and 6th Order Filters Respectively for All Subjects

2.4 sEMG信号高通滤波后的功率成分

对经过不同高通截止频率滤波后的sEMG信号进行功率谱计算（图6），在图6中，将经过20Hz高通滤波后剩余的功率成分作为标准值1，然后将其他高通截止频率滤波后剩余的功率成分与20Hz的相比，表示为相对于20 Hz高通滤波时的百分比。图5显示，对于1阶高通滤波来说，最佳的截止频率是440Hz，而在图6中，经过440 Hz高通滤波后剩余的功率成分仅为标准的20Hz高通滤波时剩余功率的2.7%。对于6阶高通滤波来说，最佳的高通截止频率为160Hz（图5）。在图6中，经过160Hz高通滤波后剩余功率成分为标准的20Hz高通滤波后剩余功率的11.6%。

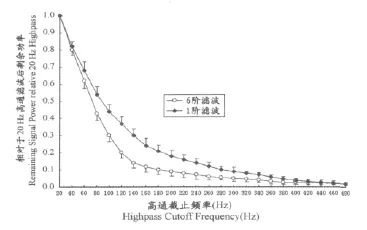
图6 本研究分别经1阶和6阶20～480Hz高通滤波后剩余的平均sEMG功率变化曲线图Figure 6. Average Remaining sEMG Signal Power after 20～480High－pass Cutoff Frequencies with 1st and 6th Order Filters

图7为1阶最佳高通滤波440Hz、6阶最佳高通滤波160Hz、1阶20Hz高通滤波、6阶20Hz高通滤波的幅频相应图，图中显示，6阶滤波时频率衰减率要明显比1阶滤波时更陡峭，1阶滤波相对平滑。

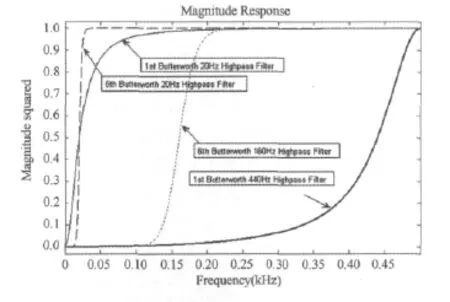
图7 1阶和6阶不同高通截止频率的幅频响应曲线图Figure 7. Characteristics of Different High－pass Cutoff Frequencies with 1st and 6th Order Filters

2.5 最佳的低通截止频率

原始sEMG信号经过20～480Hz高通滤波后，信号再进行全波整流，最后确定最佳的低通滤波截止频率和非线性标准化参数（图1），进而完成sEMG信号与力值信号的匹配（图3）。对于经过1阶不同高通滤波截止频率处理过的sEMG信号来说，最佳的低通截止频率基本在1.8Hz左右（20～480Hz高通滤波），平均为1.8±0.6Hz。而对于6阶高通滤波处理后的sEMG信号来说，最佳的低通截止频率有一个范围，从1.9±0.6Hz（360Hz高通滤波时）到2.2±0.7Hz（20Hz高通滤波时）。

2.6 最佳的非线性标准化常数

对于经过1阶高通滤波处理后的数据，最佳的非线性标准化参数（公式1）从24.6±6.3（40Hz高通滤波）逐渐降低到18.1±7.4（460Hz高通滤波）。而对于6阶高通滤波处理后的数据来说，从26.3±7.1（60Hz高通滤波）逐渐减少到17.2±6.9（360Hz高通滤波）。

3 分析

3.1 最佳的高通截止频率

使用Butterworth高通滤波后，去除原始sEMG功率的97.3%，显著地提高了基于指屈肌sEMG信号评估握力的效果，这对以前提出的应该用频率范围在10～30Hz的sEMG信号去评估肌肉力量的做法提出了质疑。从利用sEMG信号对力量预测来看，可能仅仅非常窄的频率带与力量预测有关，sEMG其余的频率成分与力量预测关系不大。

以往基于sEMG信号对力量进行预测的模型中，在对sEMG信号进行全波整流和低通滤波之前，主要采用30 Hz以下的截止频率进行高通滤波以去除动作伪迹［7］。而在本研究中，采用了更高的高通截止频率去除了原始信号中的大部分低频成分来评估肌肉力量。在肌纤维上直接产生的运动单位动作电位会比其在皮肤表面产生的sEMG信号有更大的频带范围，利用表面电极和针刺电极记录到的EMG信号产生的最高频率分别为350Hz和600 Hz［19］。因此，低频功率成分可能是由肌纤维和皮肤表面之间的信号成分被差分放大引入的，这部分信号成分并不能代表肌纤维上电信号产生的过程。如果把肌肉收缩看成是肌纤维对一个运动单位电位脉冲产生的二阶反应［12］，那么，将sEMG转换成力量的过程主要取决于sEMG的情况，因为，sEMG信号是运动单位动作电位在皮肤处叠加的结果，而运动单位电位又代表着脉冲。但是，在皮肤处记录到的sEMG信号不仅反映肌纤维处产生的运动单位电位，而且也包含着经肌纤维和表面电极之间组织滤波的信号成分以及接下来被差分放大的成分。这些因素都增加了信号的低频成分，但这些低频成分并不包含在原始的运动单位电位中［8］。如果将这些由于以上因素导致被拉长了的运动单位动作电位（低频成分增加相当于把原始的运动单位动作电位的时间跨度拉长了，即信号形状被拉长了）直接全波整流后再低通滤波，那么，有可能使力量评估不准确。

本研究的研究结果显示，sEMG经过更高截止频率进行高通滤波后去除大部分低频成分而保留sEMG中的高频率成分，能够显著降低ErrorRMS%和提高sEMG与力之间相关系数（图4，图5）。对于1阶和6阶Butterworth滤波，使用不同的高通截止频率得出相似的结果。对于1阶滤波来说，力值和sEMG信号之间得到最佳估算时，高通截止频率为440Hz，剩余的sEMG信号功率成分不到原始信号（20Hz高通滤波后的信号）的2.7%（图6）。而对于6阶滤波来说，最佳的力值和sEMG信号估算值（6阶时ErrorRMS%为8.9）与1阶时相近（1阶时 ErrorRMS%为9.1），高通截止频率为160Hz，剩余功率仅为原始的11.6%（图6）。这些数据也提示，在进行利用sEMG对力量进行预测时，采用频率要高于1 000Hz，否则很有可能使预测失败。

图6是Butterworth 1阶和6阶时不同高通截止频率滤波时的滤波特性。与6阶滤波相比，1阶滤波器的衰减率相对来说更加平缓（1阶20Hz和2阶20Hz时比较），而且越平缓越需要更高的截止频率来滤掉相同量的低频成分（1阶20Hz和1阶440Hz时比较）。6阶滤波法频率衰减率越陡，会更好地给出精确评估力量的频率。结合以上的数据来看，似乎应该滤掉160Hz以下功率成分进而来提高基于指屈肌sEMG对握力的估算。6阶滤波器滤波衰减率更加陡峭可能是造成在各个高通截止频率下ErrorRMS%以及相关系数变化更加明显／极端（图4，图5）的原因。图8显示，1阶滤波和6阶滤波相比，想要滤掉相同的低频功率成分，1阶滤波器需要使用更高的截止频率，正是由于1阶滤波和6阶滤波性能的不同，才导致了1阶滤波器最佳的高通截止频率为440Hz，而6阶滤波器最佳高通截止频率为160Hz。

3.2 处理方法的有效性分析

本研究采用不同阶数滤波器进行高通滤波滤掉低频信号成分处理时，得到了相似的结果，即最小的ErrorRMS%值相近，而且在不同面积表面电极下并没有产生显著的效应。有研究报道，表面电极大小以及两个记录电极之间的距离会影响运动单位动作电位的形状、进行影响表面肌电信号的频率成分［13］。为了观察推荐使用的高通滤波方法是否会受电极大小和电极之间距离的影响，选定了不同大小电极和电极距离作为自变量，结果发现没有显著的效应。实验中发现，使用1阶高通滤波时，18名受试者中有16名其ErrorRMS%值到440Hz之前一直在减小，直到440 Hz时达到最小；对于6阶高通滤波来说，全部18名受试者的ErrorRMS%在160Hz之前一直都在明显减小，直到160Hz时达到最小。

实际上，对肌肉力量进行精准地估算还需要知道肌肉长度以及肌肉收缩和拉长的速度。因为，肌肉收缩的长度决定着粗肌丝横桥和细肌丝结合的数目，在动力性收缩中，随着肌肉长度的变化，粗肌丝横桥和细肌丝结合的数目必定变化，从而会影响肌肉收缩时产生的力量。另外，根据Hill的肌肉力量－收缩速度关系曲线可知肌纤维收缩速度会影响肌肉力量。所以，为了准确地探究该方法预测肌力的有效性，本研究使用了静力性地等长收缩形式，而未使用动力性收缩，以排除肌肉收缩形式对评估效果的影响。同时，本实验中包含了快速收缩、慢速收缩以及长时间的最大等长收缩形式。也就是说，使用这种高通滤波方法来预测指屈肌握力是有效的。Potvin利用健康受试者肱二头肌的sEMG对肌力进行了预测，得到的最佳高通滤波截止频率与本研究相近［21］。今后还应该进一步研究不同肌纤维类型受试者以及不同皮下脂肪厚度受试者基于该方法对肌力的预测，观察是否还能得出相似的最佳滤波频率范围。

目前，在处理EMG时，还没有统一的滤波阶数限制，但是1阶到6阶之间是学者们普遍使用的范围。在本研究中，1阶滤波相对平缓，而6阶滤波相对陡峭（图7）。因此，相对来说，6阶滤波能够更加敏感地表现出频率特点，6阶滤波时最佳高通截止频率为160Hz，这似乎说明160 Hz以下的低频成分与肌力预测无关。

肌肉疲劳可能是准确预测肌力的一个较大障碍，但是，利用高通滤波滤掉大部分低频成分来预测肌力，从理论上说，这对于评价疲劳时的肌肉力量是有利的。已有研究表明，当肌肉疲劳时，大部分sEMG信号的功率成分增加的都是低频成分［3，10］，而本研究使用的高通滤波方法恰巧就是将低频成分滤掉后来预测肌力。一般来说，原始sEMG的主要频率在150Hz以下，而本研究在使用1阶和6阶高通滤波时最佳截止频率分别为440Hz和160Hz，足可以保证滤掉由于肌肉疲劳而引进的低频成分。因此，这种方法就可以避免因肌肉疲劳时带来的力值预测不准的问题。

3.3 最佳的低通截止频率

sEMG经过高通滤波滤掉无关的低频功率成分后，进行全波整流，对整流后的信号再进行低通滤波。低通滤波的目的是产生一个平滑信号更够更好地与肌力匹配（图3），单次的Butterworth低通滤波既可以去掉高频成分又能够产生相位延迟，这种相位延迟接近于肌质网与肌力之间的电机械延迟。最佳的低通截止频率取决于力值曲线与肌电曲线形状和相位的匹配程度。在本研究中，最佳的低通截止频率在1.8～2.2Hz，Olney和 Winter对下肢肌肉进行了研究，结果，最佳的低通截止频率为1.0～2.8Hz（平均1.7Hz）［15］，本研究结果在这些研究范围之内。但是Bobet与Norman研究了肘关节屈伸肌群，其低通截止频率为1.9～2.8Hz（平均为2.4Hz），同样Potvin等人研究躯干肌低通截止频率为2.4～2.9Hz，本研究结果略低于这些学者的研究结果。在本研究中，采用2Hz低通滤波后，sEMG信号曲线并没有像力值曲线那样平滑，当低通截止频率值越低，sEMG信号曲线虽然越平滑，但是相位延迟却更大了，从而使sEMG曲线与力值曲线的RMS误差更大。因此，从本研究结果来看，2Hz左右的低通截止频率能使sEMG曲线与力值的形状和相位延迟上得到较好的匹配。

3.4 最佳的非线性标准化常数

在本研究中，所有受试者指屈肌的sEMG与力值都呈现非线性关系（图2），在以前的报道中有的肌肉sEMG与力 值 呈 现 非 线 性 关 系［9，11，20，24，26］，而 有 的 肌 肉 呈 现 线 性 关系［24，26］。Fuglevand等人认为，不同肌肉产生的差别可能与运动单位冲动的发放行为有关［12］。在本研究中，非线性程度与处理方法有关，主要与不同高通截止频率值有关。随着高通截止频率的增加（20～480Hz），平均非线性常数表现为降低（25.2～17.4），这说明，随着高通截止频率的增加，处理后的sEMG与力值之间的非线性程度减弱，也就是说，去除更多的低频成分后，使指屈肌sEMG与指屈肌产生的握力之间非线性程度减弱了。这些结果提示，除了运动单位的募集与发放行为导致了力电之间的非线性外，皮下组织的滤波过程可能也是导致两者呈现非线性的另一个重要原因。

4 结论

本研究采用高通滤波的方法滤掉原始信号中90%～95%的成分后，提高了对指屈肌收缩力的估算能力，这对以往使用10～30Hz高通截止频率滤波作为最佳截止频率来预测肌力提出了质疑。通过去除sEMG中的低频伪迹成分而留取高频成分能够更好地代表发生在肌纤维处的电生理特性。

本研究有一个限制，就是在令受试者指屈肌握电子拉力计收缩时，电子拉力计是固定不动的。因此，收缩时指屈肌长度是不变的，属于静力性的等长收缩，因此，以后的研究可以针对不同肌纤维类型肌肉、不同收缩长度、动力性收缩、不同皮下脂肪厚度（这些因素都会影响sEMG信号的频率成分）进行研究。

［1］郭峰，张日辉.优秀女子拳击运动员后手直拳技术动作上肢肌肉表面肌电分析［J］.沈阳体育学院学报，2009，28（4）：65－68.

［2］郭峰，张日辉，唐光大.优秀女子拳击运动员后手直拳动作鞭打技术分析［J］.北京体育大学学报，2011，34（1）：45－47.

［3］ALLISON G T，FUJIWARA T.The relationship between EMG median frequency and low frequency band amplitude changes at different levels of muscle capacity［J］.Clin Biomech，2002，17（6）：464－469.

［4］ARENDT－NIELSEN L，MILLS KR.Muscle fiber conduction velocity，mean power frequency，mean EMG voltage and force during submaximal fatiguing contractions［J］，Muscle Nerve，1989，12（6）：493－497.

［5］ARSLAN YZ，ADLI MA，AKAN A，et al.Prediction of externally applied forces to human hands using frequency content of surface EMG signals［J］.Comput Methods Programs Biomed，2010，98（1）：36－44.

［6］CHOLEWICKI J，VANVLIET J J.Relative contribution of trunk muscles to the stability of the lumbar spine during isometric exertions［J］.Clin Biomech，2002，17（2）：99－105.

［7］CLANCY EA，MORIN F，MERLETTI R.Sampling，noise－reduction and amplitude estimation issues in surface electromyography［J］.J Electromyogr and Kinesio，2002，12（1）：1－16.

［8］DE LUCA C J.The use of surface electromyography in biomechanics［J］.J Appl Biomech，1997，13：135－163.

［9］DEL SANTO F，GELLI F，GINANNESCHI F，et al.Relation between isometric muscle force and surface EMG in intrinsic hand muscles as function of the arm geometry［J］.Brain Res，2007，1163：79－85.

［10］DIDERIKSEN J L，FARINA D，ENOKA R M.Influence of fatigue on the simulated relation between the amplitude of the surface electromyogram and muscle force［J］.Philos Transact A Math Phys Eng Sci，2010，368（1920）：2765－2781.

［11］DOLAN P，ADAMS M A.The relationship between EMG activity and extensor moment generation in the erector spine muscles during bending and lifting activities［J］.J Biomech，1993，26（4－5）：513－522.

［12］FUGLEVAND A J，WINTER D A，PATLA A E.Models of recruitment and rate coding organization in motor－unit pools［J］.J Neurophysiol，1993，70（6）：2470－2488.

［13］FUGLEVAND A J，WINTER D A，PATLA A E，et al.Detec－tion of motor unit action potentials with surface electrodes：influence of electrode size and spacing［J］.Biol Cybern，1992，67（2）：143－153.

［14］GRANATA K P，ORISHIMO K F，SANFORD A H.Trunk muscle coactivation in preparation for sudden load［J］.J Electromyogr Kinesio，2001，11（4）：247－254.

［15］KAMAVUAKO E N，FARINA D，YOSHIDA K，et al.Relationship between grasping force and features of single－channel intramuscular EMG signals［J］.J Neurosci Methods，2009，185（1）：143－150.

［16］LAURSEN B，JENSEN B R，NEMETH G，et al.A model predicting individual shoulder muscle forces based on relationship between electromyographic and 3Dexternal forces in static position［J］.J Biomech，1998，31（8）：731－739.

［17］MADELEINE N P，BAJAJ P，SOGAARD K，et al.Mechanomyography and electromyography force relationships during concentric，isometric and eccentric contractions［J］.J Electromyogr Kinesiol，2001，11（2）：113－121.

［18］MARRAS W S，DAVIS K G，MARONITIS A B.A non－MVC EMG normalization technique for the trunk musculature：part 1.Model development［J］.J Electromyogr Kinesio，2001，11（1）：1－9.

［19］NILSSON J，PANIZZA M，HALLET M.Principles of digital sampling of a physiologic signal［J］.Electro Clin Neurophys，1993，89（5）：349－358.

［20］POTVIN J R，NORMAN R W，MCGILL S M.Mechanically corrected EMG for the continuous estimation of erector spine muscle loading during repetitive lifting［J］.Eur J Appl Physiol，1996，74（1－2）：119－132.

［21］POTVIN J R，BROWN S H M.Less is more：high pass filtering，to remove up to 99%of the surface EMG signal power，improves EMG－based biceps brachii muscleforce estimates［J］.J Electromyogr Kinesio，2004，14（3）：389－399.

［22］RANTALAINEN T，KLODOWSKI A，PIITULAINEN H.Effect of innervation zones in estimating biceps brachii force－EMG relationship during isometric contraction［J］.J Electromyogr Kinesio，2012，22（1）：80－87.

［23］SEMMLER J G，TUCKER K J，ALLEN T J，et al.Eccentric exercise increases EMG amplitude and force fluctuations during submaximal contractions of elbow flexor muscles［J］.J Appl Physiol，2007，103（3）：979－989.

［24］SCHMITT K，DELLORUSSO C，FREGOSI R F.Force－EMG changes during sustained contractions of a human upper airway muscle［J］.J Neurophysiol，2009，101（2）：558－568.

［25］WINTER D A.Biomechanics of human movement with applications to the study of human locomotion［J］.CRC Crit Rev Biomed Eng，1999，9（4）：287－314.

［26］WOODS J，BIGLAND－RITCHIE B.Linear and non－linear surface EMG－force relationships in human muscles［J］.Am J Phys Med，1983，62（6）：2873－2899.