交集运算在读图中的应用研究

王小娟，赵洪生，吴亚先

（1.晋城职业技术学院 机械与电子工程系，山西 晋城048026；2.太原理工大学 机械工程学院，太原030024）

二维视图一直是工科传统的工程图表达方法，也是当前最为成熟，且不可替代的表达方法。然而近年来，随着计算机技术的发展，三维技术逐步走向成熟，得到了越来越广泛的应用。相比二维工程图而言，三维模型更加直观，也更便于人们使用计算机技术对其进行设计与分析。由二维工程图实现三维模型的重建，一直是近年来图形学工作人员努力的研究目标。虽然有些三维软件提供了“二维转三维”的模块（如Solidworks）［1］，但并不能实现其模型由二维到三维的自动重建。同时，也有一些二次开发的“二维转三维”模块投入应用［2－3］，但实际效果也并不理想。

对于一类由柱体通过“交集”运算，或者部分由“交集”和“差集”运算得到的集合体（组合体）［4］，在大多数情况下，使用一种简单、快速、有效的方法，利用二维工程图中的两个视图，使用布尔“交集”运算，可以实现其三维模型的快速重建。这种方法并不要求我们从三维的角度去思考，而是从二维的角度去判断与编辑，然后实施三维建模。笔者将基于AutoCAD软件对这一问题进行深入探讨。

1 基本原理

如图1中所示，对于一个初学者来说，迅速地构建其三维实体并不是一件容易的事。但其实，我们只要利用三维软件，分别拾取主视图与俯视图的最外轮廓线作为草图，分别从宽度方向和高度方向拉伸成柱体，然后对两个柱体求“交集”，即可得到其三维模型。

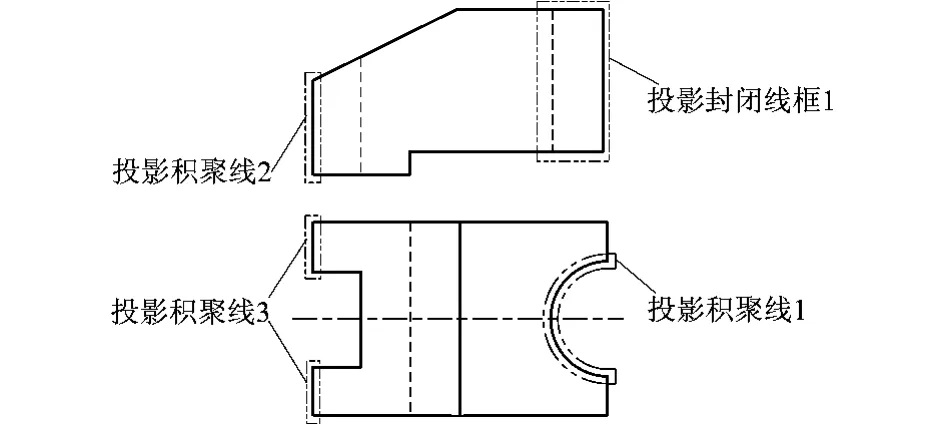
图1 例1二维二视图

这是一个可以使用布尔“交集”命令，利用二维二视图快速重建其三维模型的典型例子。其实，这样的组合体并不在少数，在我们经常见到的组合体中占有相当大的比重。对于这一类的组合体，我们可以在对其三维模型没有任何概念的情况下，遵循一定的方法与步骤，利用其二维二视图实现其三维模型的重建。这样，对于这类组合体的三维模型重建变得简单而快速，这就为这类组合体的三维模型自动重建提供了一种理论上的可能。同时，我们可以利用其三维模型得到其其余视图，这也就为初学者提供了一种有效的学习方法，可以用来训练自己的空间思维、完成制图练习等等。

2 方法

下面，我们将利用AutoCAD软件，系统地阐述这一问题。首先，我们将从二维视图的角度出发，阐述如何判断组合体是否适用于这种方法，给出其二维二视图需要满足的条件。接下来，我们将介绍这种方法的过程与步骤。

2.1 二维判断条件

实体，我们可以理解为由表面围成的封闭空间区域。当一个组合体的所有表面（无论是平面、柱面、曲面）已经确定时，这个组合体就是确定的。其实，一个组合体的所有表面的空间位置确定时，每个表面的形状（边界）也就确定了，从而组合体也就确定了。这里将分3步从二维图的角度来判断、限定这类组合体。

1）判断组合体的任一表面是否都可垂直于某一投影面。一个面垂直于投影面，其投影会是一条积聚线，这时这个面是可以由这条线拉伸得到的。也唯有这种情况才有可能由这个投影面上的投影积聚线拉伸得出这个面。进而，一个组合体，唯有任一表面（包括内孔面）都可垂直于某一投影面，才有可能通过拉伸得到其所有表面。判断方法是使用线面分析法，利用三面投影关系“长对正、高平齐、宽相等”［5］，找到各个视图中相对应的一组投影封闭线框［6］和投影积聚线。若至少有一个视图上的投影是一条积聚线，那么这个表面就是垂直于这个投影面的，即这个面可以由这条积聚线拉伸得到。例如图1主视图中的投影封闭线框1，对应于俯视图中的投影积聚线1，由此判断该表面垂直于水平投影面；再如俯视图中的投影积聚线3，对应于主视图中投影积聚线2，由此判断该表面垂直于两投影面。如此逐一判断每个表面是否可垂直于某一投影面。再来看图2中的例子，主视图中的投影封闭线框1，对应于左视图中的投影封闭线框2，该表面无投影积聚线，故该平面不垂直于正投影面与侧投影面。而图3中，投线影封闭线框1对应于投影积聚线1，故该平面垂直于正投影面。

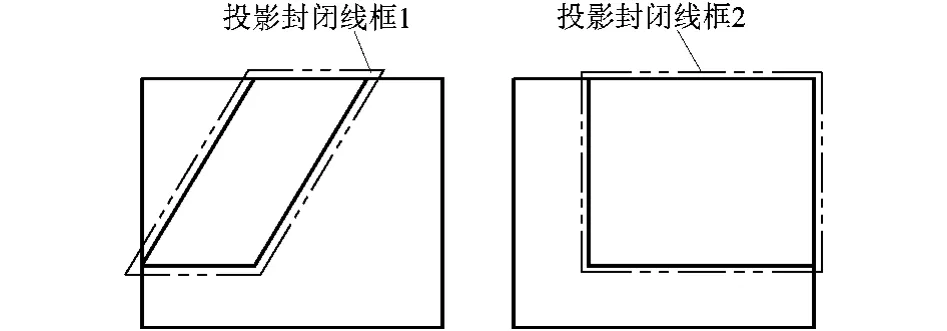
图2 例2二维二视图

2）判断组合体是否有内孔。通常内孔在与其垂直的投影面上的投影，为一位于相应视图内部且相对独立的封闭线框，且大都为圆框（内孔大都为圆孔）。在其余视图上为两条虚线（直线或是折线）与其余线组成的封闭线框。这样就可以判断组合体是否存在内孔（区分组合体是否有内孔，是因为两者在使用此方法时略有区别）。例如图4中的组合体，其俯视图内部有一个圆框，相对独立于其他线条。其在主视图中相对应的投影为两条平行的虚线。由此我们判断此组合体存在一个内孔。

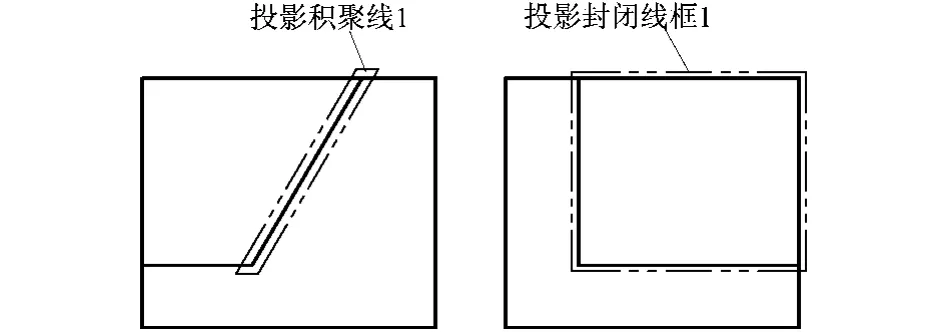
图3 例3二维二视图

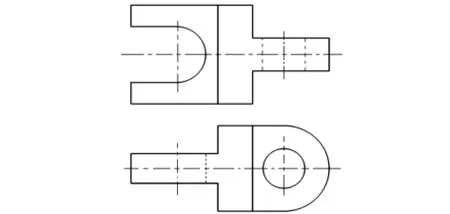
图4 例4二维二视图

3）判断组合体是否适用于此方法。纵然一个组合体的所有表面都可由一条积聚投影线拉伸得到，但未必每个表面的积聚投影线都可直接投影在某一视图的最外轮廓线上。这样，该表面就不可由某一视图的最外轮廓线拉伸得到。判断方法是利用步骤1找到的相对应的一组投影元素，判断是否存在至少一条投影积聚线位于该视图的最外轮廓线上。如此逐一检查每个表面的一组投影，保证每个表面都可在某一视图的最外轮廓线上找到该表面的一条投影积聚线。

例如，图1中的投影封闭线框1与投影积聚线1，投影积聚线1位于俯视图的最外轮廓线上。再如投影积聚线2与投影积聚线3，两条投影积聚线都位于该视图的最外轮廓线上。再来看图3中的例子，投影封闭线框1所对应的投影积聚线1不在该视图的最外轮廓线上，故该组合体不适用于该方法。

若组合体存在内孔，则内孔必须是直孔时此方法才适用（与内孔数量无关）。直孔在两个视图上的投影是一封闭线框与两条平行的虚线。例如，图4中的组合体，我们可以判断出该圆孔为直孔。

2.2 过程与步骤

下面我们将以图1和图4中的组合体为例解释说明建模过程［7］。

1）拾取最外轮廓线，绘制面域。执行“面域（region）”，分别拾取各个视图的最外轮廓线，绘制成各个视图相对应的面域。

若组合体存在内孔，在绘制与内孔面相垂直的投影面上的面域时，执行“面域（region）”，分别拾取最外轮廓线与各内孔的轮廓线，绘制成各个相互独立的面域。然后执行“差集（subtract）”，从最外轮廓线面域中减去各个孔的面域。所得面域即为该视图的面域。例如图4中的组合体执行“面域”操作后如图5所示，执行“差集”操作后如图6所示。

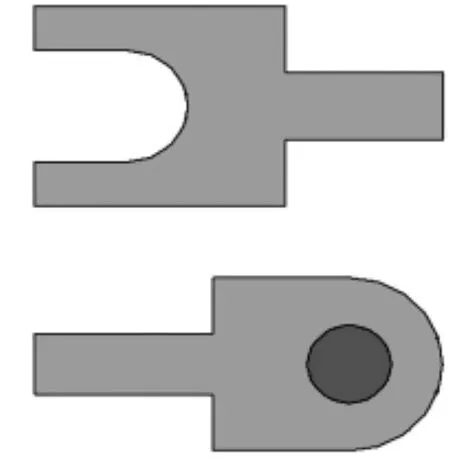
图5 面域操作1

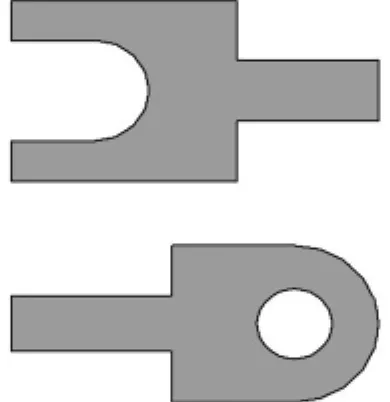
图6 面域操作2

2）创建新图纸，粘贴面域。创建新图形文件，执行“视图／视口／四个视口”，将视口改为如图7所示。单击左上角的视口，执行“视图／三维视图／主视”，将该视口改为主视。如此，将右上角视口改为左视，左下角视口改为俯视，右下角视口改为西南等轴测。这样设置更方便于我们观察与操作。然后，复制各视图最外轮廓线面域，粘贴到相应的视图视口。根据三面投影关系“长对正、高平齐、宽相等”，移动各视图最外轮廓线面域到合适的位置。对图1和图4中例子分别执行该操作后如图7和图8所示。

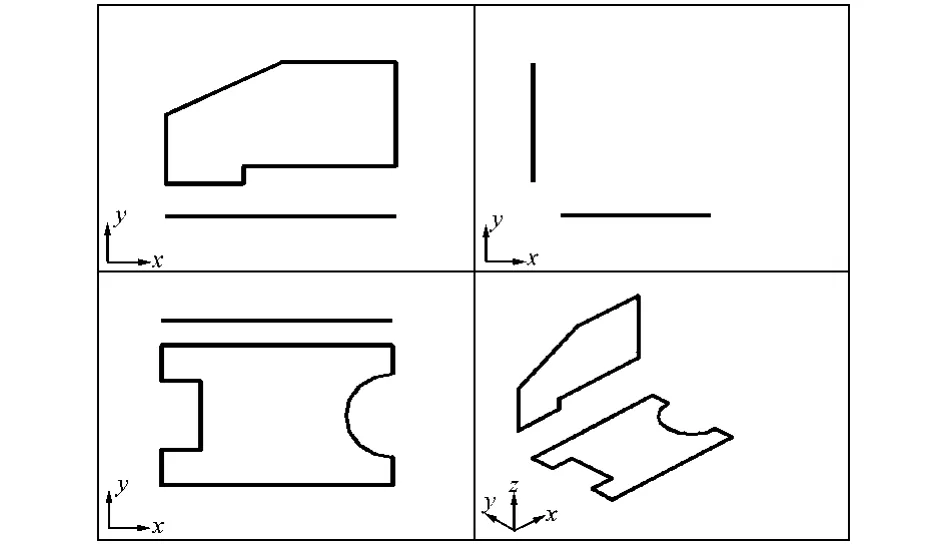
图7 例1面域设置完成

图8 例4面域设置完成

3）拉伸面域成柱体，执行“交集”运算，完成建模。执行“拉伸（extrude）”，分别拾取各最外轮廓线面域沿垂直方向拉伸成柱体（柱体的高度没有限制，以超过其余最外轮廓线面域边界为准）。对图1和图4中例子分别执行该步骤后如图9和图11所示。

执行“交集（intersect）”，拾取所有柱体，右击完成交集运算，完成建模。对图1和图4中例子分别执行该步骤后如图10和图12所示。

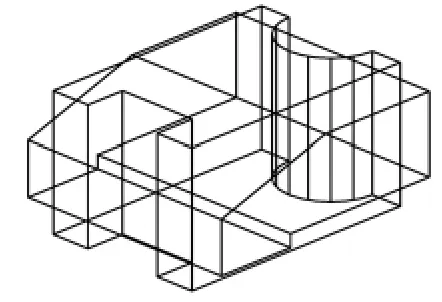
图9 例1柱体拉伸完成

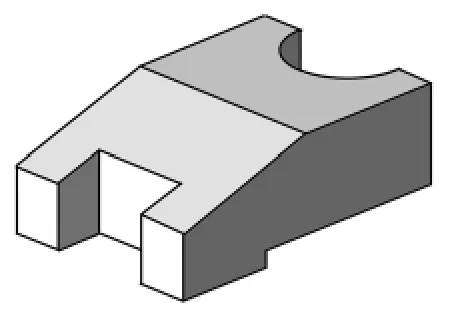
图10 例1三维模型

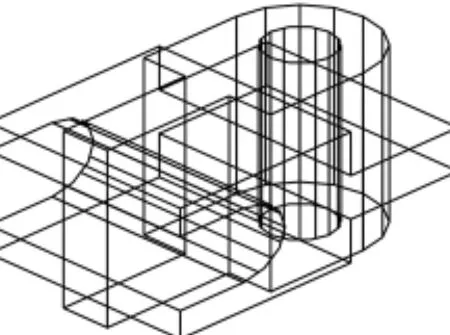
图11 例4柱体拉伸完成

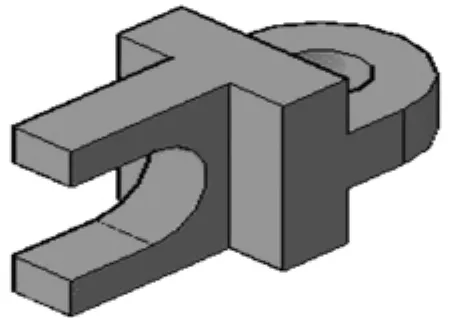
图12 例4三维模型

建模完成后，会自动在主视图视口、左视图视口、俯视图视口生成三视图。我们可以利用“着色”、“三维动态观察器”等工具条观察、检查三维模型与三视图。我们也可以在布局空间中输出其三视图与任意方向的轴测视图［4］，从而可以通过对比现在视图与原有视图的区别，检查建模是否正确。我们也可以通过此方法补全第三投影面视图。图1中例子建模完成后，输出其三视图与西南等轴测视图如图13所示。

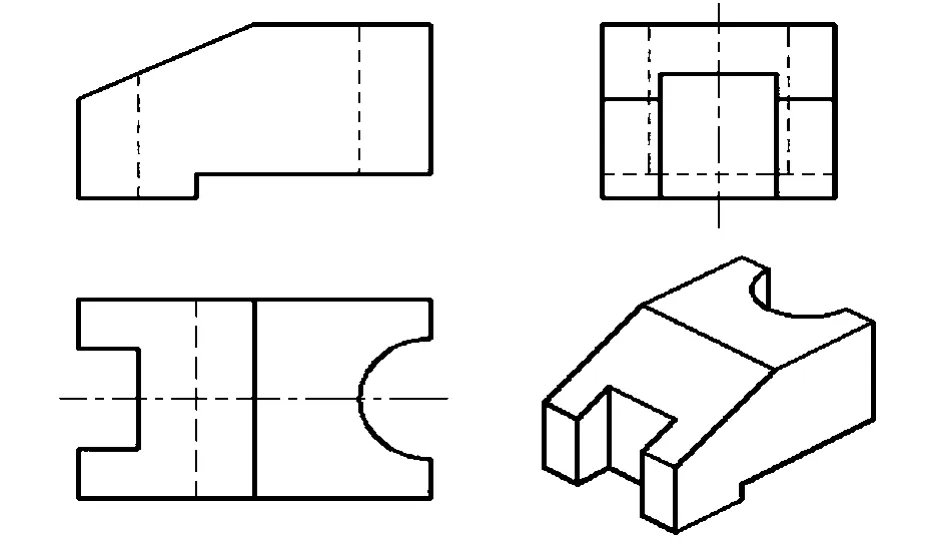
图13 由三维模型重生成的二维三视图

接下来再看下面的例子。请看图14中的例子，初看并不好想象其三维形状，直接建立其三维模型也比较复杂。但我们用前文中的二维判断准则判断一下，此组合体是可以用此方法实现其三维模型的快速重建的。对图14的二维二视图执行步骤1）、

2）之后，得如图15所示；完成面域拉伸后得如图16 所示，建模完成后得如图17所示。

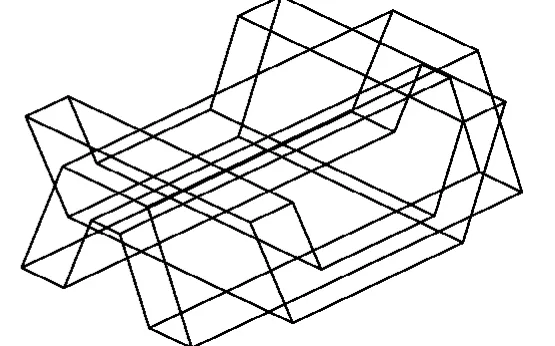
图16 例5柱体拉伸完成

图15 例5面域设置完成

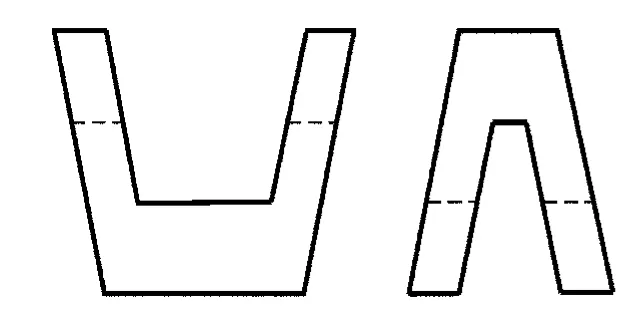
图14 例5二维二视图

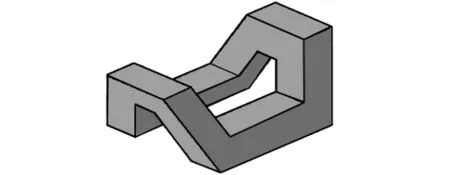
图17 例5三维模型

3 结束语

经过大量的实例验证，在重建此类主要由柱体通过“交集”运算得到的集合体的三维模型时，此方法具有一定的通用性。在重建许多比较复杂的组合体时，此方法可以有效简化三维模型重建的步骤，提高重建的速度。这也正是我们所期望的一种结果。同时，此方法也对组合体的三维模型自动重建提供了一种新的思路。这里需要指出的是，虽说此方法只适用于这类组合体，但对于许多其他组合体，我们只需对其进行简单的分解与改造，就可以变成一个或几个这样的组合体，从而实现该方法的灵活应用。在这里，我们期待此方法的修改与完善，也期待着此方法的进一步发展与应用。

［1］ 乔春蓉，赵伟民.Solidworks中二维图形与三维模型的互化问题研究［J］.佳木斯大学学报（自然科学版），2007，25（6）：777-778.

［2］ 张晓.基于 AutoCAD的三视图快速转换三维立体图的方法［J］.软件导刊，2010，9（5）：192-193.

［3］ 李晋芳，施法中.商品化CAD软件中基于二维视图的三维重建模块的设计与实现［J］.计算机辅助设计与图形学学报，2005，17（4）：795-799.

［4］ 杨胜强.现代工程制图［M］.北京：国防工业出版社，2001：130-134.

［5］ 李勇峰，陈书剑.线面分析法在组合体读图中的应用［J］.科技信息，2009（32）：121-124.

［6］ 韩丽艳，张孟玫，孙轶红.利用三维CAD成型法进行组合体读图的研究［J］.北京石油化工学院学报，2009，17（4）：48-50.

［7］ 王国顺，袁晓洲，李伟.AutoCAD基础教程［M］.北京：高等教育出版社，2008：108-111.