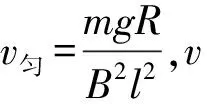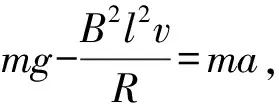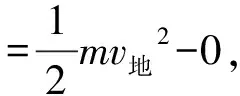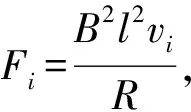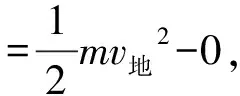对一道电磁感应题目全面严谨的分析

张秀梅

(复旦大学附属中学，上海 200433)

众所周知,中学里电磁感应的题目综合性强,涉及到动力学、电路、能量、动量等知识,有的问题运动过程多样,而且常常是变加速运动,解决它需要的物理思维和综合分析能力都很强．本文要解决的就是这种运动过程多样复杂的问题,要全面、严谨分析本题并不容易,笔者曾经跟许多高中名校的教师讨论,多数教师认为分析解决该题超出了高中物理范围,王溢然主编的《中学生思维丛书·猜想与假设》的书上也认为“从动态特性上做一般分析超出了中学物理知识的范畴”．笔者找到了以高中物理知识为基础进行全面分析的方法．可以看到,复杂背后的简单是物理规律永恒的美．解决本题用的图像法、微元累加法在解决其他问题时也可以使用．

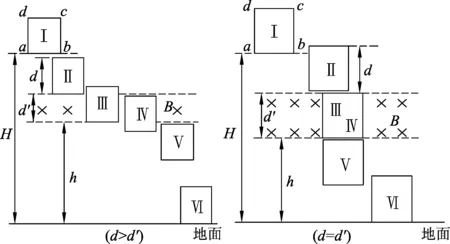
如图1所示,矩形线框abcd在竖直平面内,其下方有一个有界的水平匀强磁场,边ab、cd和磁场的边界都水平,线框平面与磁感线垂直．线框从离地高H处由静止开始自由下落,穿过匀强磁场、完全出磁场后落地,ab边落地速度为v1．若将磁场向上平移一小段距离,如图2所示,让线框仍从离地H高度由静止开始自由下落,ab边落地时速度为v2,试比较v1与v2之间的大小关系．

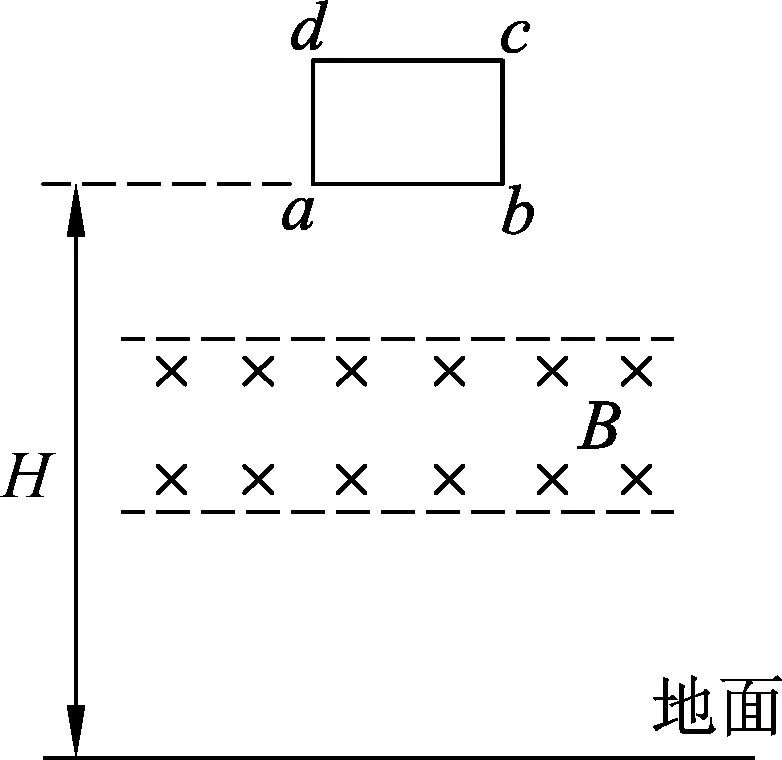
图1 图2

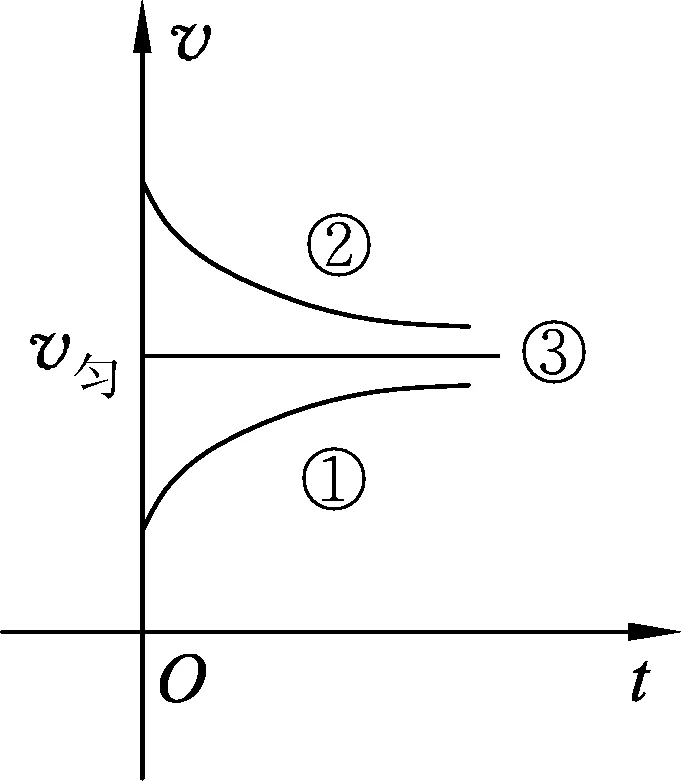
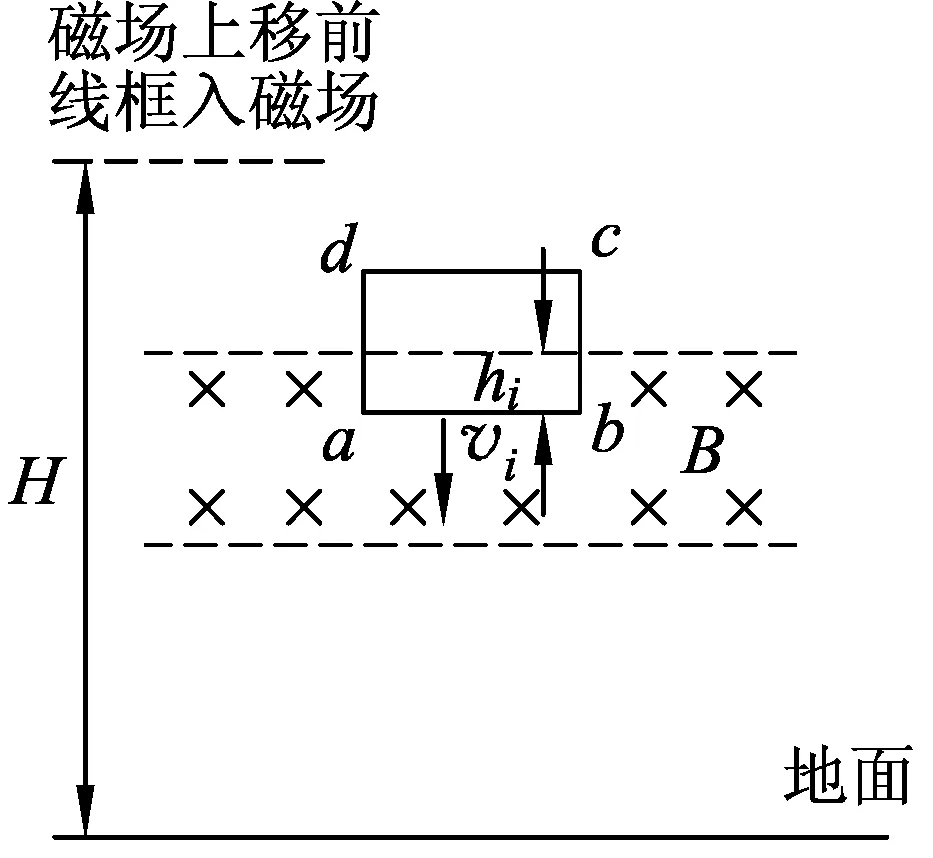
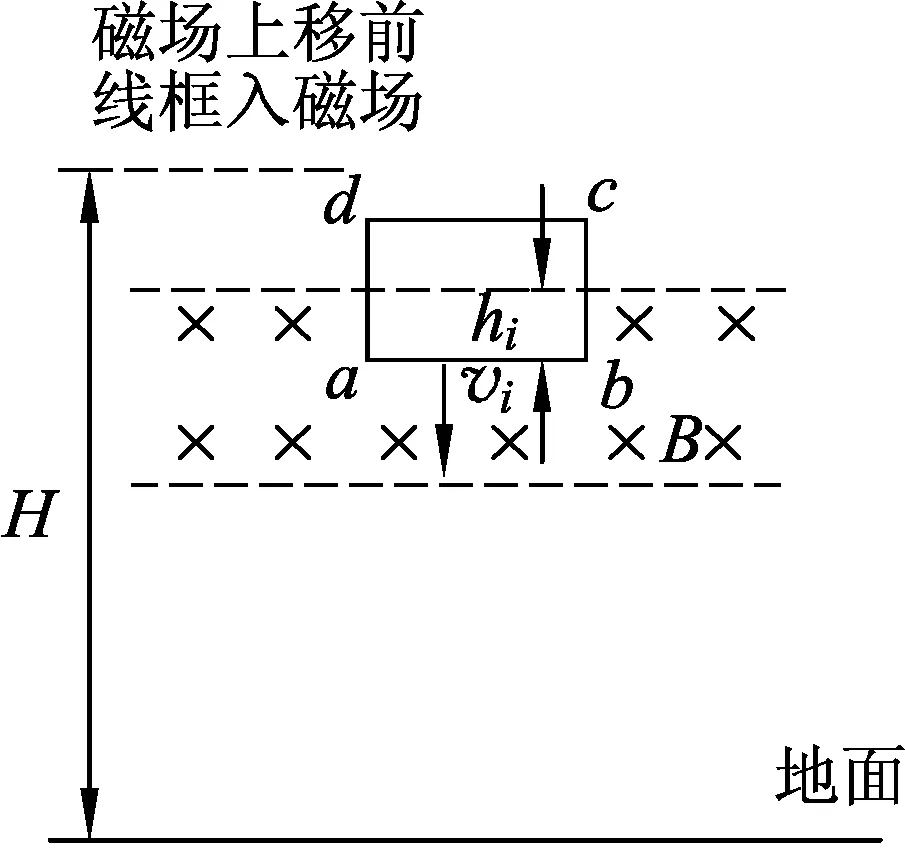
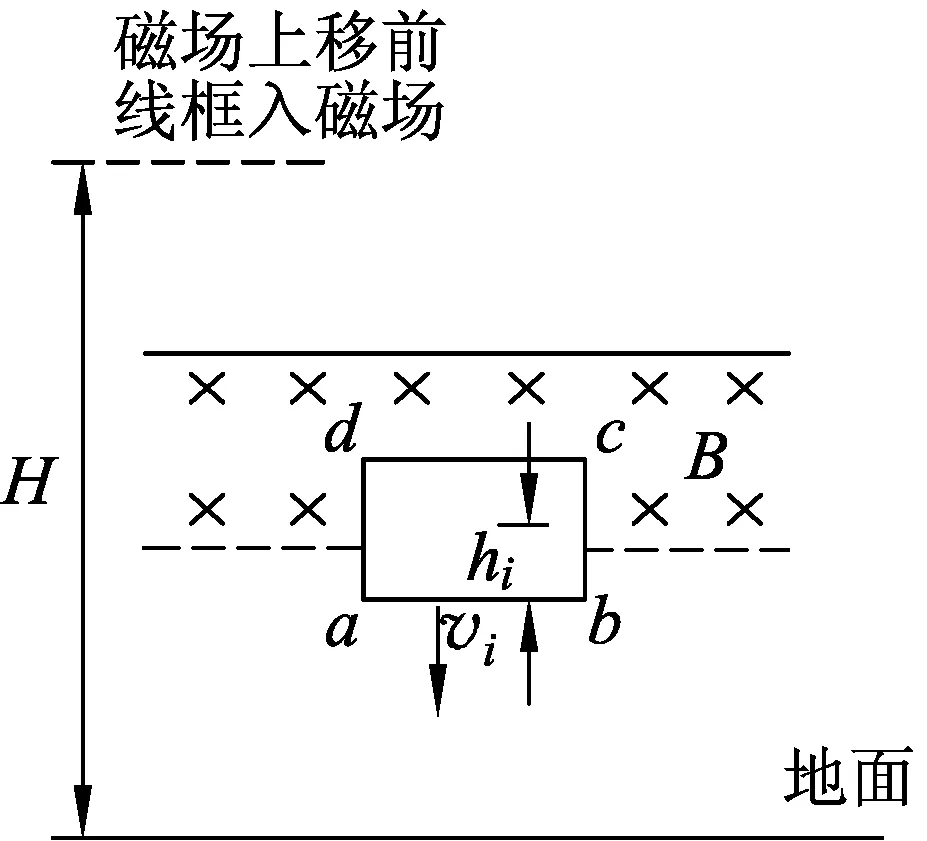
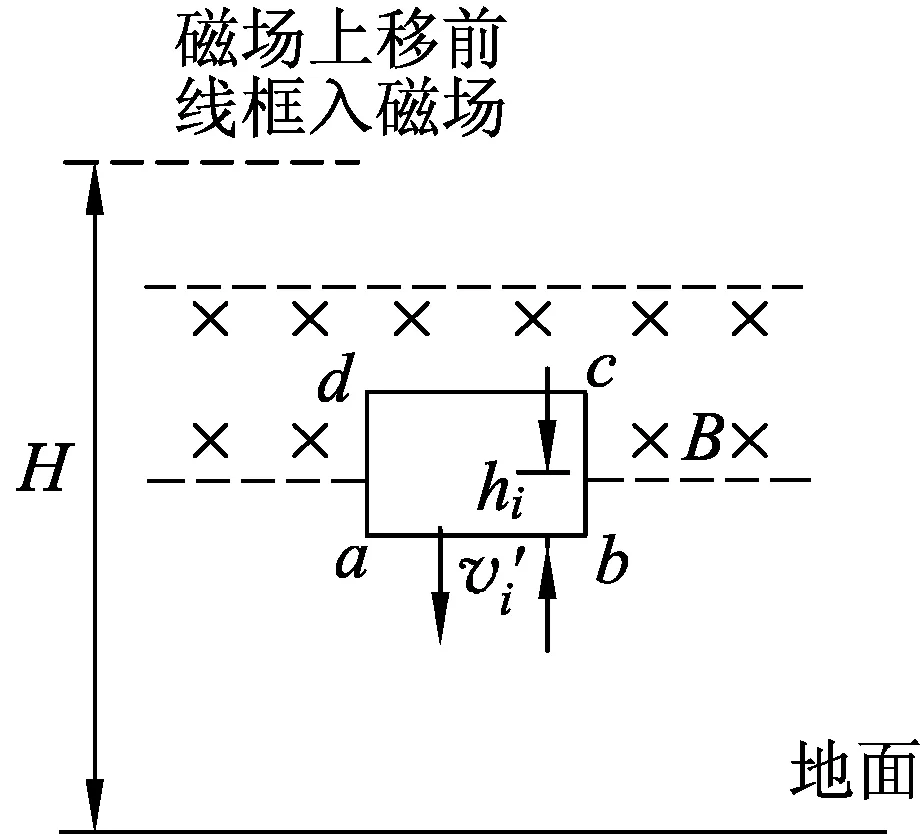
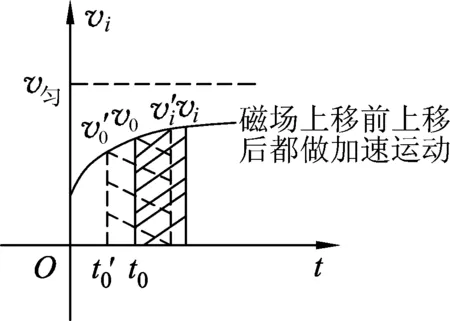
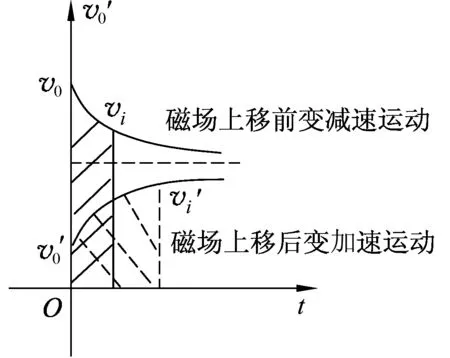
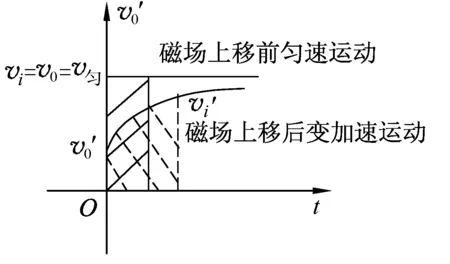
(A)v2>v1. (B)v2

(C)v2=v1. (D) 条件不足,无法确定.

分析:设线框质量为m,边长ab=cd=l,宽度ad=bc=d,电阻为R,匀强磁场磁感应强度为B,磁场宽度为d′．

图3

图4

线框到达Ⅱ的速度与Ⅰ→Ⅱ阶段的高度有关,到达Ⅳ的速度则与之前的3个阶段的运动都有关,由于图3中的H、d、d′的尺度都不确定,因此,在线框穿越过程中,入磁场和出磁场的运动存在多种组合．如果入磁场加速,则出磁场可能加速、减速或匀速;如果入磁场匀速,则出磁场可能减速或匀速;如果入磁场减速,则出磁场可能减速或匀速．

另一方面,磁场上移后线框入磁场的运动与上移前入磁场的运动也存在相关性．磁场上移后,线框从图3中的位置Ⅰ→Ⅱ自由落体运动的高度减小,线框入磁场的初速度就比上移前小,受到的安培力也就比磁场上移前小,因此,如果磁场上移前线框入磁场做加速运动或者匀速运动,则磁场上移后线框做加速运动;如果磁场上移前线框入磁场做减速运动,则磁场上移后线框入磁场做加速运动、匀速运动、减速运动均有可能．

这样看起来本题相当复杂繁琐．但请相信:物理规律是复杂现象背后的简单.

为了叙述方便,以下把线框下落过程中,磁场上移前与上移后边ab相对于磁场边界相同距离的位置称为对应位置．图5和图6中的hi相等,两线框位置就是线框入磁场的磁场上移前与上移后的某

图5

图6

一对应位置,同样图7和图8是线框出磁场时的某一对应位置．磁场上移前和上移后,线框对应位置的速度分别记作vi和vi′．

图7

图8

图9

再看磁场上移前线框入磁场做变减速运动的情形,图10、11、12分别对应了磁场上移后做变减速运动、变加速运动和匀速运动的图像,由图像可见都是vi′

图10

图11

图12

图13

图3中线框从位置Ⅲ到位置Ⅳ,磁场上移后和上移前线框位移相同,加速度也都是重力加速度,所以线框出磁场的初速度是磁场上移后小于磁场上移前．

用分析线框入磁场运动的同样的方法可以得到,线框出磁场的末速度也是磁场上移后比上移前小,也就是图(3)中位置Ⅴ的即vⅤ′

线框完全出磁场最后Ⅴ→Ⅵ的运动阶段,磁场上移前、后加速度都是g,磁场上移后初速度比上移前小(vⅤ′

再考虑用动能定理研究．

如果线框做变加速或者做变减速运动的阶段,安培力是变力,求克服安培力做功需要用微元累加法．当然,不管安培力是恒力还是变力都可以用元功累加法求全过程克服安培力做的功．

图14

同理可得:线框出磁场阶段克服安培力做的功也是磁场上移后比上移前小．

有些题目要比较线框下落的时间,再用动量定理分析即可．

与本题有类似运动过程的题目在不少书上都有收录．比如:宋淑光主编的《上海新高考等级考·物理总复习》,王溢然编著《中学生思维丛书·猜想与假设》．由于题目是选择题,书上介绍的方法往往是猜想、排除法．但是,总有优秀学生会质疑:结论是不是对线框所有的情况都成立呢?题目有没有错误?既然多本中学物理书上出现,我们最好不要以一句“超出了中学物理知识的范畴”去回答．挑战难题、严谨全面的分析是应该有的科学态度,而且这样的态度会影响我们学生的．笔者也期待老师们能给出更简单、全面、严谨的方法!