关于二项式系数级数恒等式

及万会, 黑宝骊



关于二项式系数级数恒等式

及万会, 黑宝骊

(银川能源学院 基础部, 宁夏 银川, 750105)

根据一个已知级数, 使用裂项方法得到分母含有1到5个因子的二项式系数级数. 所给出二项式系数级数的和式是封闭形的, 并给出二项式系数数值级数恒等式. 裂项的方法研究二项式系数变换是组合分析的新手段, 也是产生新级数的一个初等方法.

二项式系数; 裂项; 级数; 封闭形; 恒等式

1 主要结论与证明

定理1 a. 分母含有1个因子的二项式系数级数恒等式.

b. 分母含有2个因子乘积的二项式系数级数恒等式.

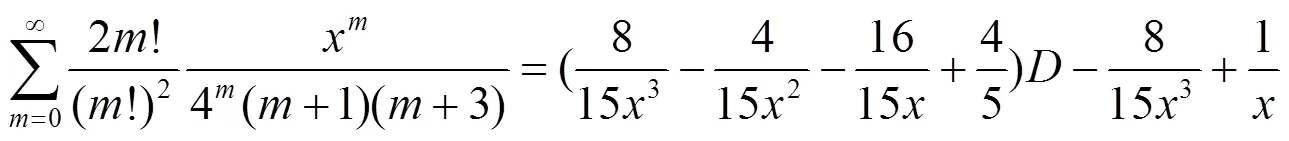
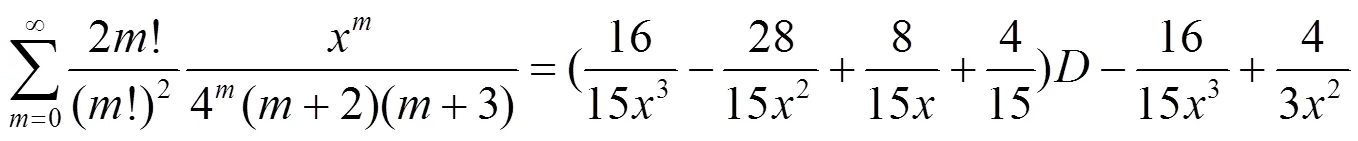
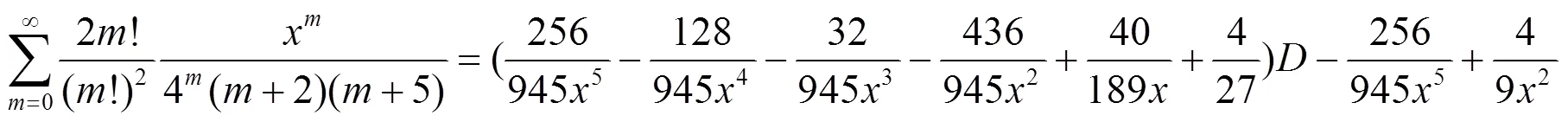
c. 分母含有3个因子乘积的二项式系数级数恒等式.

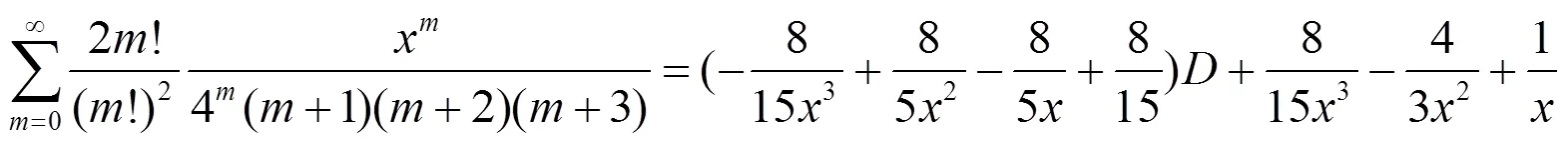
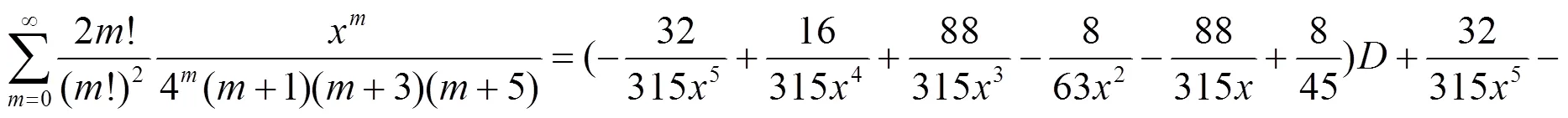
d. 分母含有4个因子乘积的二项式系数级数恒等式.

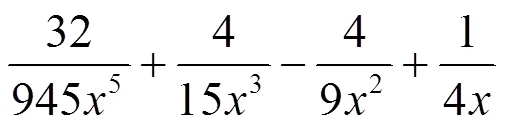
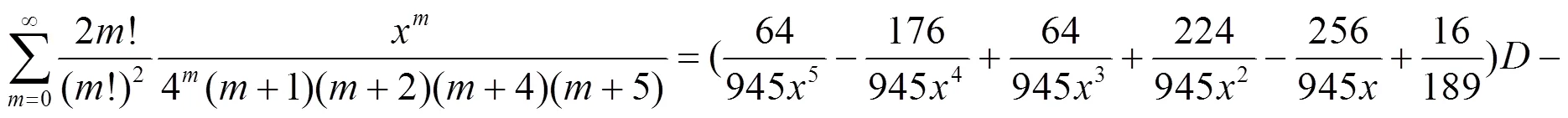
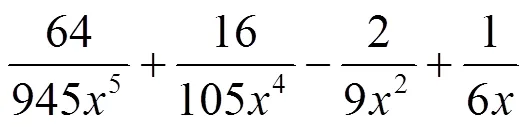
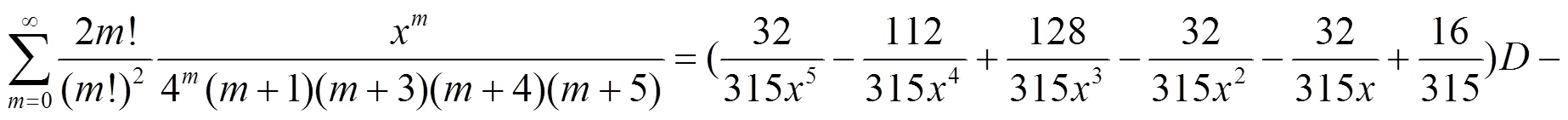
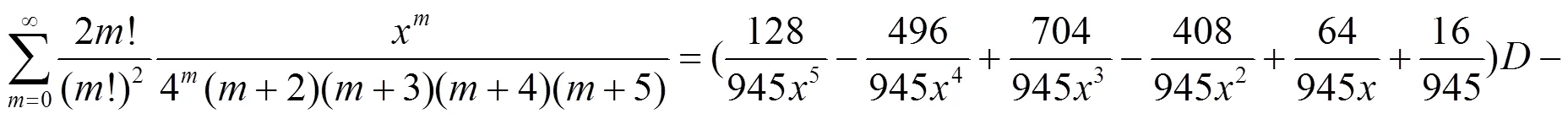
e. 分母含有5个因子乘积的二项式系数级数恒等式.

证明 a. 对级数(1)式左端裂项:

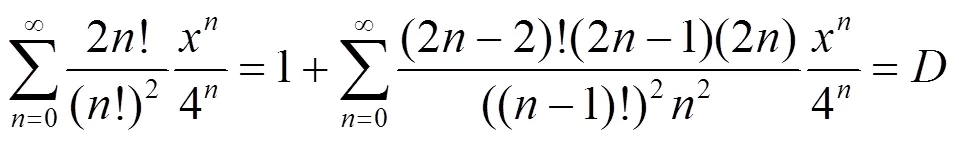
整理得到(2)式.

即:

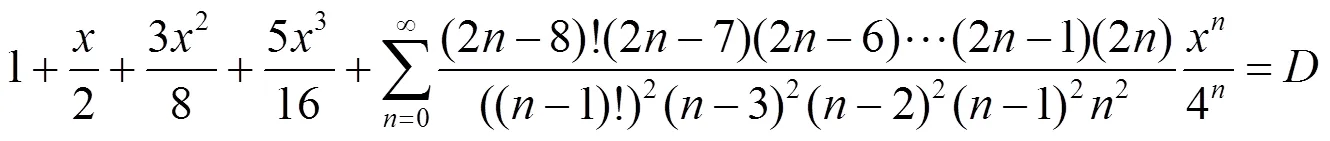
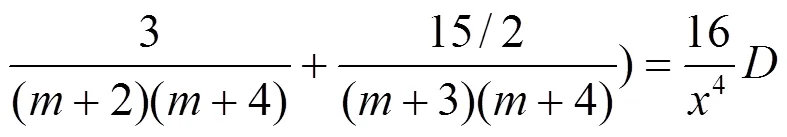
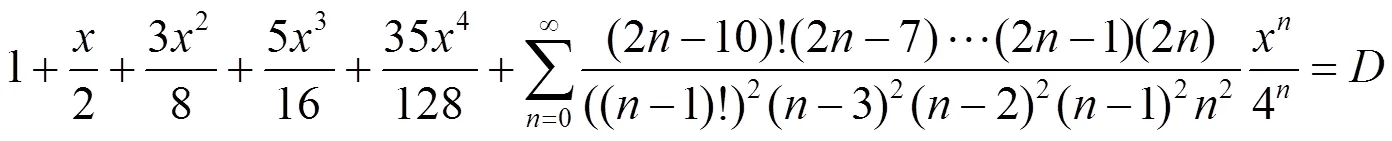
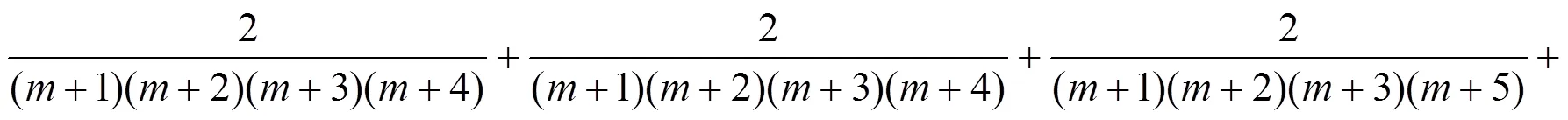
在(36)式中含有2个因子的分式10个, 3个因子的分式有10个, 4个因子的分式有5个, 5个因子的分式1个, 对(36)式实行下列运算得到分母含有1, 2, 3, 4个因子的组合数的恒等式.

(a) 将(36)式的所有含有因子的分式化成部分分式, 得:

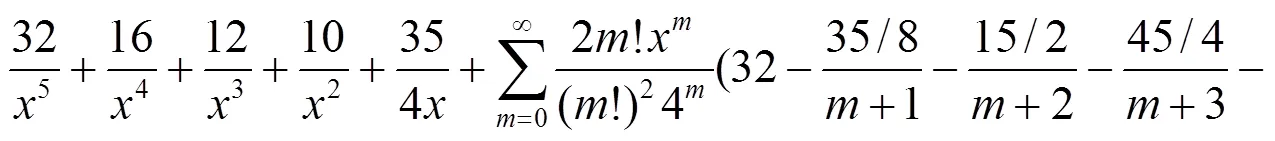
(b) 对于(36)式, 首先保留2个因子的分式, 其他分式化成部分分式.其次对这些2个因子的分式, 每次保留1个, 其余化成部分分式, 得到:

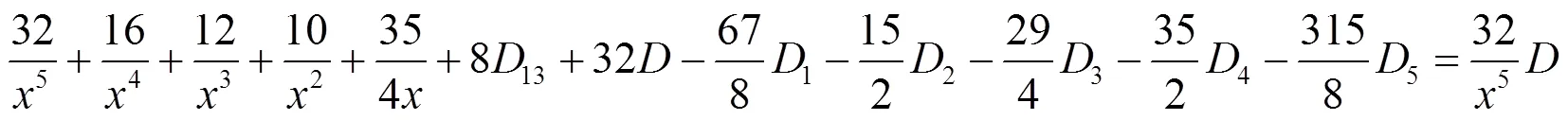
(c) 对于(36)式, 首先保留3个因子的分式, 其他分式化成部分分式. 其次对这些3个因子的分式, 每次保留1个, 其余化成部分分式, 得到:

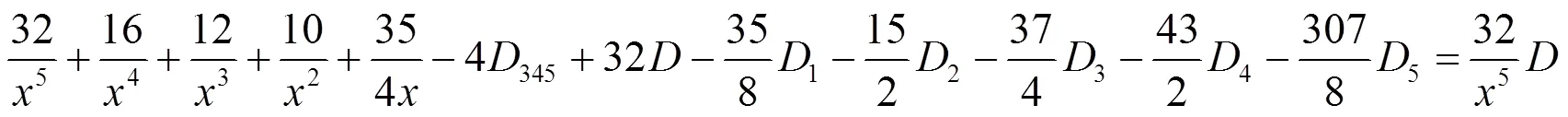
(d) 对于(36)式, 首先保留4个因子的分式, 其他分式化成部分分式. 其次对这些4个因子的分式, 依次保留1个, 其余化成部分分式, 得到:

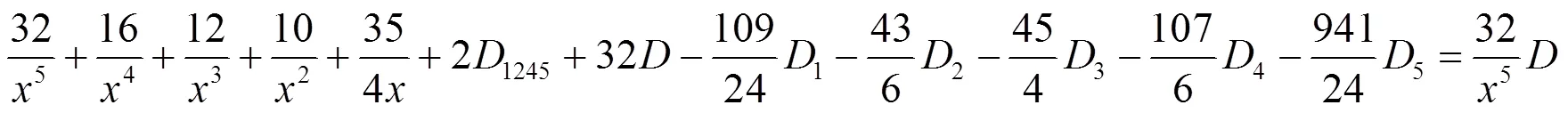
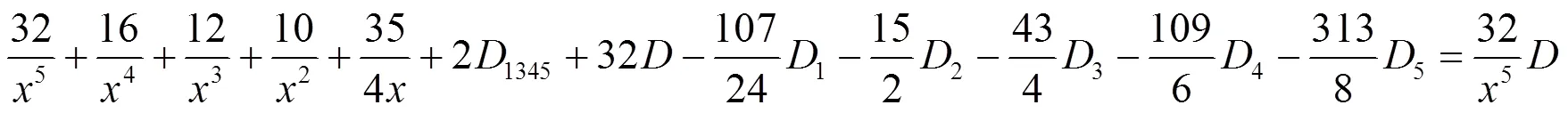
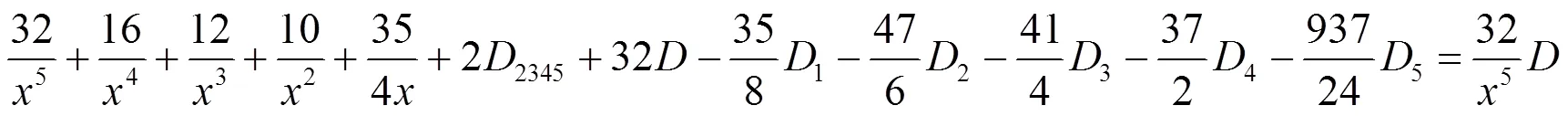
(e) 对于(36)式, 首先保留5个因子的分式, 其他分式化成部分分式, 得到:

2 推论

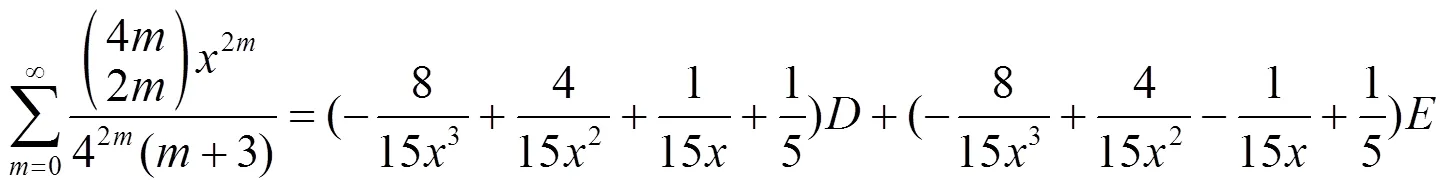
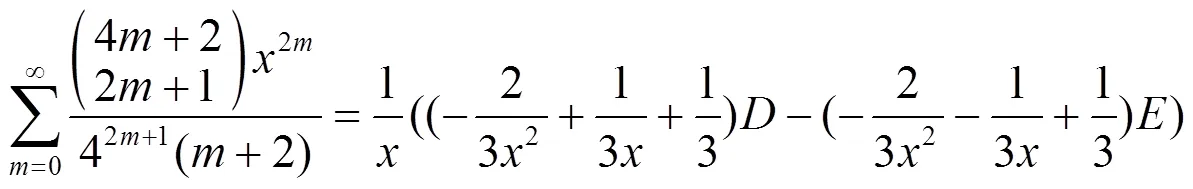
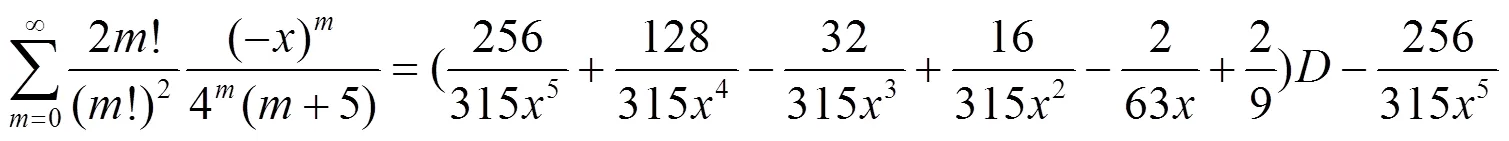
3 数例

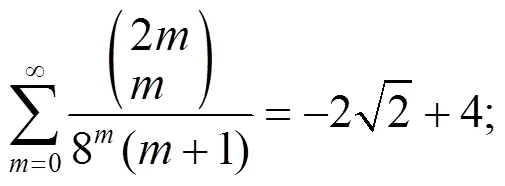
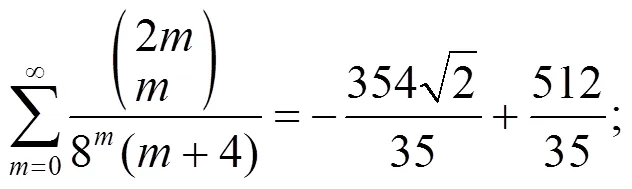
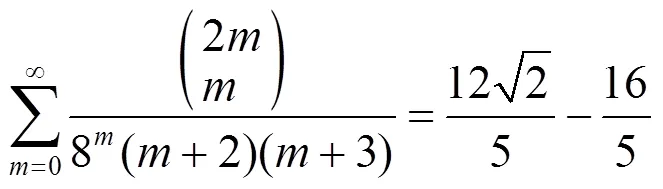
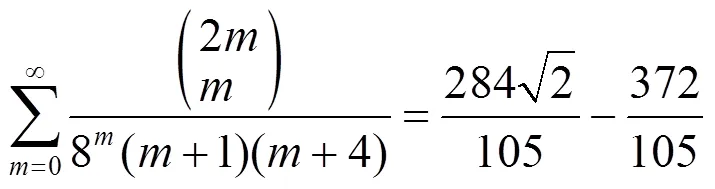
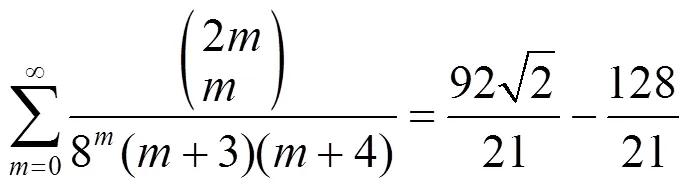
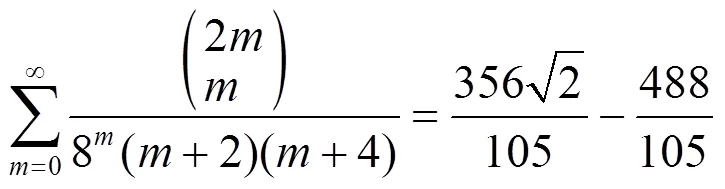
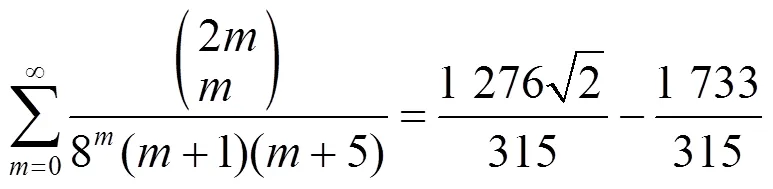
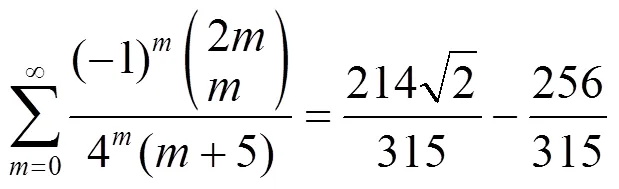
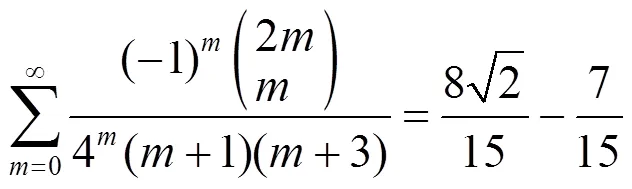
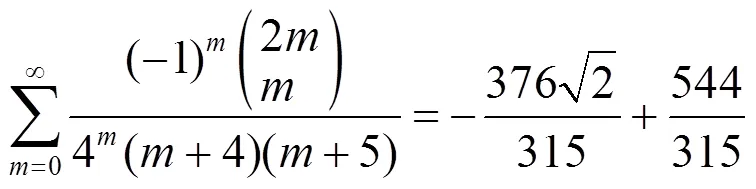
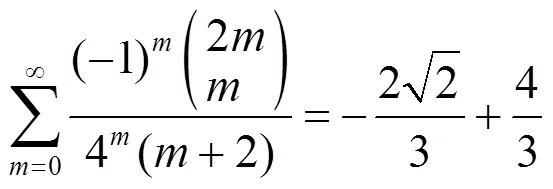
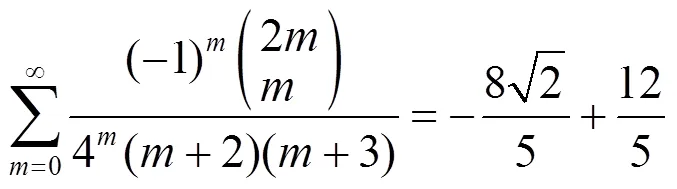
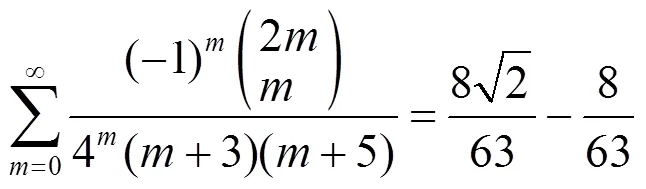
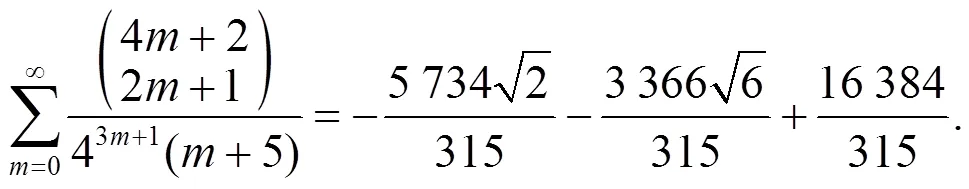
[1] Sury B, Wang T N, Zhao F Z. Some identities involving of binomial coefficients[J]. Journal of Integer Sequences, 2004, 7(2): 1-12.

[2] Sofo A. General properties involving reciprocal of Binomial coefficients[J]. Journal of Integer Sequences, 2006, 9(4): 1-13.

[3] Sprugnoli R. Sums of reciprocal of the central binomial coefficients[J]. Integral: Electronic Journal of Combinatorial Number Theory, 2006, 6: 1-17.

[4] Yang J H, Zhao F Z. Sums involving the inverses of binomial coefficients[J]. Journal of Integer Sequences, 2006, 9(4): 1-11.

[5] Borwein J M, Girgensohn R. Evaluation of binomial series[J]. Aequationens Math, 2005, 70: 25-36.

[6] Amghibech S. On sum involving Binomial coefficient[J]. Journal of Integer Sequences, 2007, 10(2): 1-4.

[7] 编写组. 数学手册[M]. 北京: 人民教育出版社, 1979: 226

On one class series identities of binominal coefficients

JI Wan-hui, HEI Bao-li

(Department of Basic, Yinchuan Energy College, Yinchuan 750105, China)

Using one known series, several new series of binominal coefficients were gotten by splittingitems. These denominators of series contains different the multiplication of one to five factors and binominal coefficients, and some identities of series of numbers values of binominal coefficients were put forward. The method ofsplititems offered in this paper was a new combinatorial analysis way and a elementary method to construct new series.

binomial coefficients; split terms; series; form closed; identity

O 173

1672-6146(2012)04-0004-010

10.3969/j.issn.1672-6146.2012.04.002

2012-09-24

银川能源学院科研基金项目(2011-37-15)

及万会(1942-), 男, 教授, 研究方向为数论. E-mail: jiwanhui2008@163.com

(责任编校: 刘晓霞)