三维电阻抗成像的测量模式

王化祥，黄文瑞，范文茹

(1. 天津大学电气与自动化工程学院，天津 300072；2. 中国民航大学航空自动化学院，天津 300300)

电阻抗成像(electrical impedance tomography，EIT)技术通过对被测对象施加驱动电流/电压，并测量被测场域周围的响应信息，从而重建其内部电学参数(如电导率、介电常数)分布的图像．EIT不仅用于多相流检测，同时还应用于医学临床诊断，如肺通气[1]、心脏容量的改变[2]、胃排空[3]、头部成像[4]以及乳腺癌检测[5]．根据应用的场合，对电极采用不同的激励模式，如相邻激励、相对激励和准对向激励等．一旦得到了边界测量值，即可建立适当的模型，反演组织内电学参数的分布．

建模和图像重建的大部分研究都是围绕 2D展开的，实际上，3D电学成像技术能够提供更精确的组织场分布．目前，3D建模和图像重建已经取得突破进展，虽然计算上更加复杂但也更精确[6]．3D图像重建的发展，关键在于确定出合适的激励(驱动)／测量模式，这对指导硬件系统的设计、提高测量精度和改善重构图像质量等方面具有重要意义．2007年，Graham和 Adler[7]指出，双层 16电极 EIT系统使用平面型电极配置(即本文的同层相邻驱动)进行 3D EIT肺部成像效果最佳．本文在此基础上，进一步探讨了 EIT的测量模式，通过建立 3D有限元模型(finite element model，FEM)，提出并评价了2种用于3D EIT的测量模式．

1 实验方法

1.1 模 型

本文利用大型有限元仿真软件 COMSOL Multiphysics 3.5a建,立 EIT系统模型并计算敏感场参数．物理模型采用的是双层 24电极模型，如图 1(a)所示，并通过软件自动划分网格的功能得到了155,277个三角形单元构成的有限元模型，如图1(b)所示．圆柱形容器的半径为 32,cm、高为 96,cm，内部盛满 1,S/m 的介质．电极是半径为 3,cm、高为 3,cm的圆柱形电极，分别放置在高度为30,cm和66,cm的2个平行平面上．

图1 双层24电极EIT模型Fig.1 Two-layer 24-electrode EIT model

1.2 激励模式

本文选用了4种典型的激励模式，激励电流均为1,mA．

同层相邻驱动和同层准对向驱动，这2种驱动方法是2D EIT常用的激励模式，由于被激励电极对取自同一层电极，故称为同层驱动．

方型驱动(按照图 1(a)中 1-2-14-15-3-4的顺序激励)和折线型驱动(按照图 1(a)中 1-14-2-15-3-16的顺序激励)，这2种激励模式是双层电极EIT特有的激励方法，因为被激励电极对可能取自不同层电极．

1.3 测量模式

3D EIT测量边界电压的方法与2D EIT不同．对于双层电极 EIT，测量相邻电极之间的电势差，既可以是测量同层相邻电极之间的电势差(简称同层测量)，也可以是测量不同层相邻电极之间的电势差(简称不同层测量)．同层测量与 2D EIT的测量方法类似，不同层测量在本文中按照电极激励的顺序重新为电极号排序，然后按照排序后的电极号，测量所有电极号相邻的电极之间的电势差．对于折线型不同层测量，测量值总是取自不同层的相邻电极；对于方型不同层测量，测量值一半取自同层的相邻电极，一半取自不同层的相邻电极．

同时，测量边界电压应避开驱动电极．对于同层驱动模式，剩余的电极阵列往往不具有如折线型或方型这样规则的形式，故同层驱动模式不宜搭配不同层测量模式．

综上所述，本文对比评价的激励/测量模式的组合包括同层相邻驱动(同层测量)、同层准对向驱动(同层测量)、方型驱动同层测量/不同层测量，折线型驱动同层测量/不同层测量共6种．

1.4 评价步骤

6种不同模式分别用3个仿真实验进行评价：垂直和径向运动实验以及不同电导率实验．垂直运动实验是在圆柱形容器底面径向距离 20,cm处放置一个小圆柱体，垂直移动小圆柱体使它从容器底部运动到顶部，如图 2(a)所示．径向运动实验是在圆柱形容器中心处放置一个小圆柱体，沿容器半径方向水平移动小圆柱体使它从容器中心运动到边缘，如图 2(b)所示．不同电导率实验是在圆柱形容器轴线上放置 2个形状相同、电导率不同的小圆柱体，高度为 64,cm的小圆柱体电导率较高为 10,S/m，高度为 32,cm 的小圆柱体电导率较低为 0.1,S/m，如图 2(c)所示．小圆柱体的尺寸均为半径5,cm，高度20,cm．

图2 3组对比实验Fig.2 Three contrast experiments

对于垂直和径向运动实验，分别选取小圆柱体运动到4个不同位置的时刻做截面成像；对于不同电导率实验仅进行一次截面成像．圆柱形容器的高度为96,cm，电极平面的高度为30,cm和66,cm．

1.5 评价指标

评价和比较图像重建基于以下5个标准．

1)敏感场的灵敏度和均匀性

电学成像系统中，敏感场分布通常是非均匀的．以灵敏度系数矩阵中元素的标准差和均值的比值[8]作为评价敏感场分布的指标．

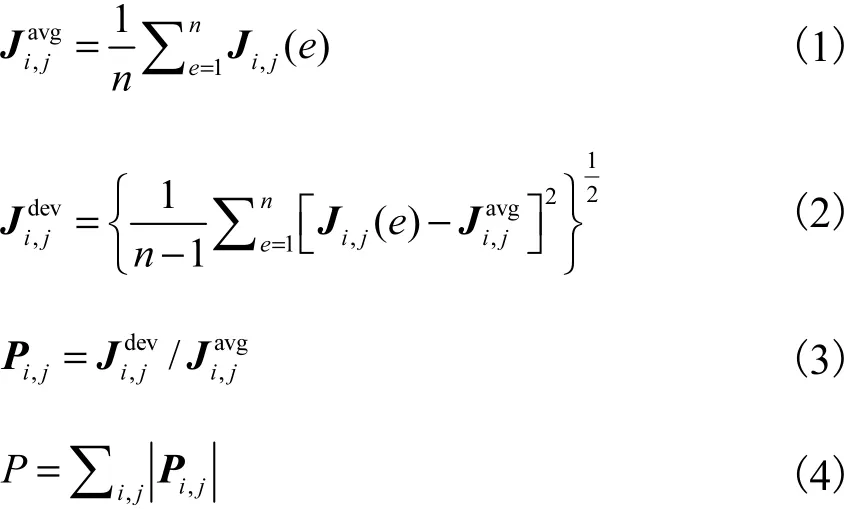
2)独立测量数

对灵敏度系数矩阵进行奇异值分解，可得每种模式的独立测量数[7]为

3)边界电压值

通常，数据采集要求边界电压测量值尽可能大，并希望测量值的范围小．定义边界电压的动态范围[9]为

式中 VMax和 VMin分别为一次实验中边界电压值取绝对值后的最大值和最小值．显然，D值越小，边界电压的动态范围越小．鉴于介质分布变化前后，边界电压值的变化不大，故本文仅比较了空场时的边界电压值及动态范围．

4)分辨力

分辨力反映了系统对场域内物质改变的敏感程度．对于 EIT系统，分辨力是场域内有目标和无目标时边界电压差的范数与激励电流的范数的比值[10]，即

式中：I为激励电流；V1和 V2分别为空场和有物体时的边界电压值．显然，d值越大，系统的分辨能力越强．

5)重建图像的相关度

通常，以相关度作为对重建图像定量评估的指标[8]，其计算式为

2 实验结果

2.1 评价实验

1)敏感场的灵敏度和均匀性

如表1所示，折线型驱动同层测量模式的敏感场分布最差，折线型驱动不同层测量模式的敏感场分布最理想．

表1 矩阵J的分布和奇异值数Tab.1 Distribution and singular values of Jacobian matrix

2)独立测量数

如表 1所示，同层准对向驱动、方型驱动同层测量和折线型驱动同层测量模式的奇异值数较高，而同层相邻驱动、方型驱动不同层测量和折线型驱动不同层测量模式的奇异值数相对较低．

3)边界电压值

如表 2所示，不同层测量的模式，其边界电压平均值明显大于同层测量的模式．

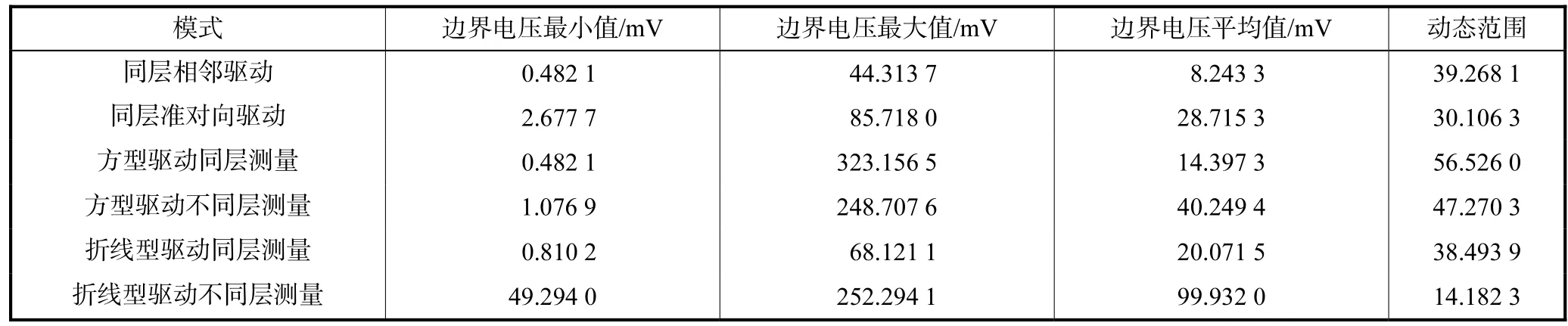
表2 边界电压值Tab.2 Amplitude of boundary voltage

4)分辨力

如图3和表3所示，不同层测量的模式，其分辨物体的能力明显优于同层测量的模式．

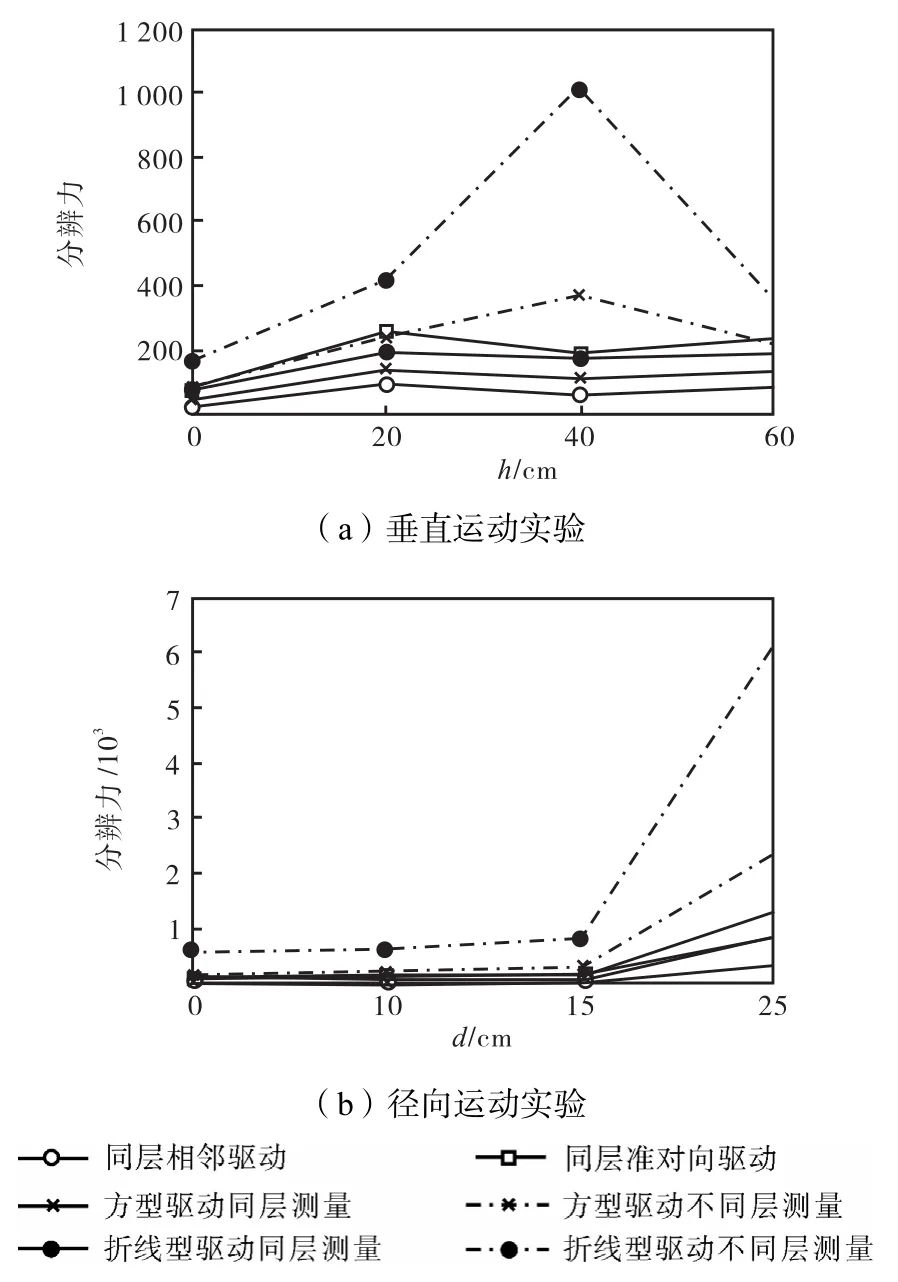
图3 垂直运动和径向运动实验中的分辨力Fig.3 Resolution of radial position and vertical position experiments

表3 不同电导率实验中的分辨力和相关程度Tab.3 Resolution and qualitative evaluation of different conductivity experiments

5)重建图像的定量评估

如图4和表3所示，在前2个实验中，同层测量的模式相关程度较好；不同电导率实验中只有方型驱动同层测量较理想．

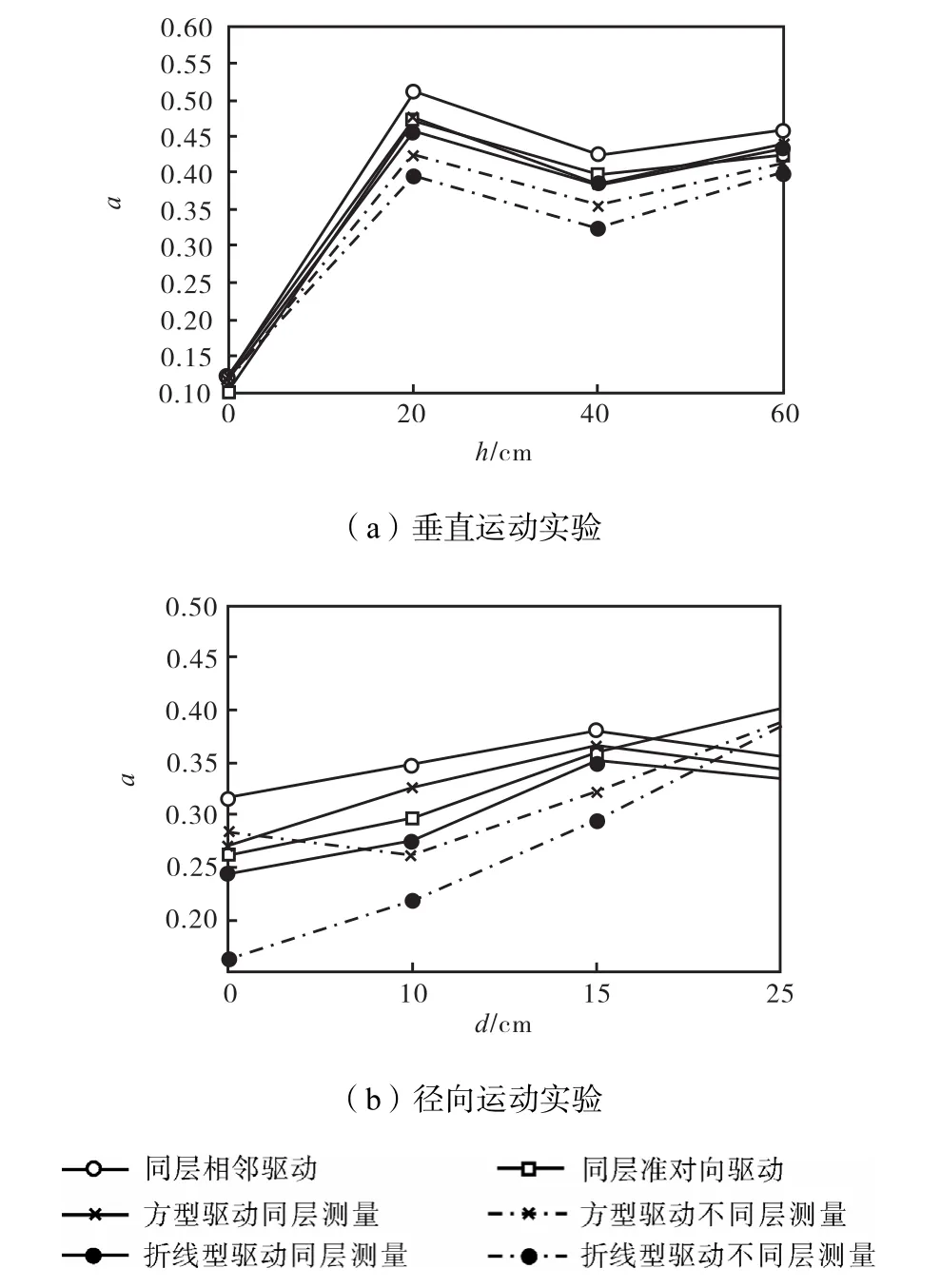
图4 垂直运动和径向运动实验中的相关程度Fig.4 Qualitative evaluation of radial position and vertical position experiments

2.2 重建图像

表4为垂直运动实验中，基于共轭梯度算法迭代50次的几幅重建图像．

结果表明，当物体运动至两电极平面之间区域时，成像较准确．其中，2种不同层测量的图像暗淡，区分度不明显．同层相邻驱动的图像质量较高．

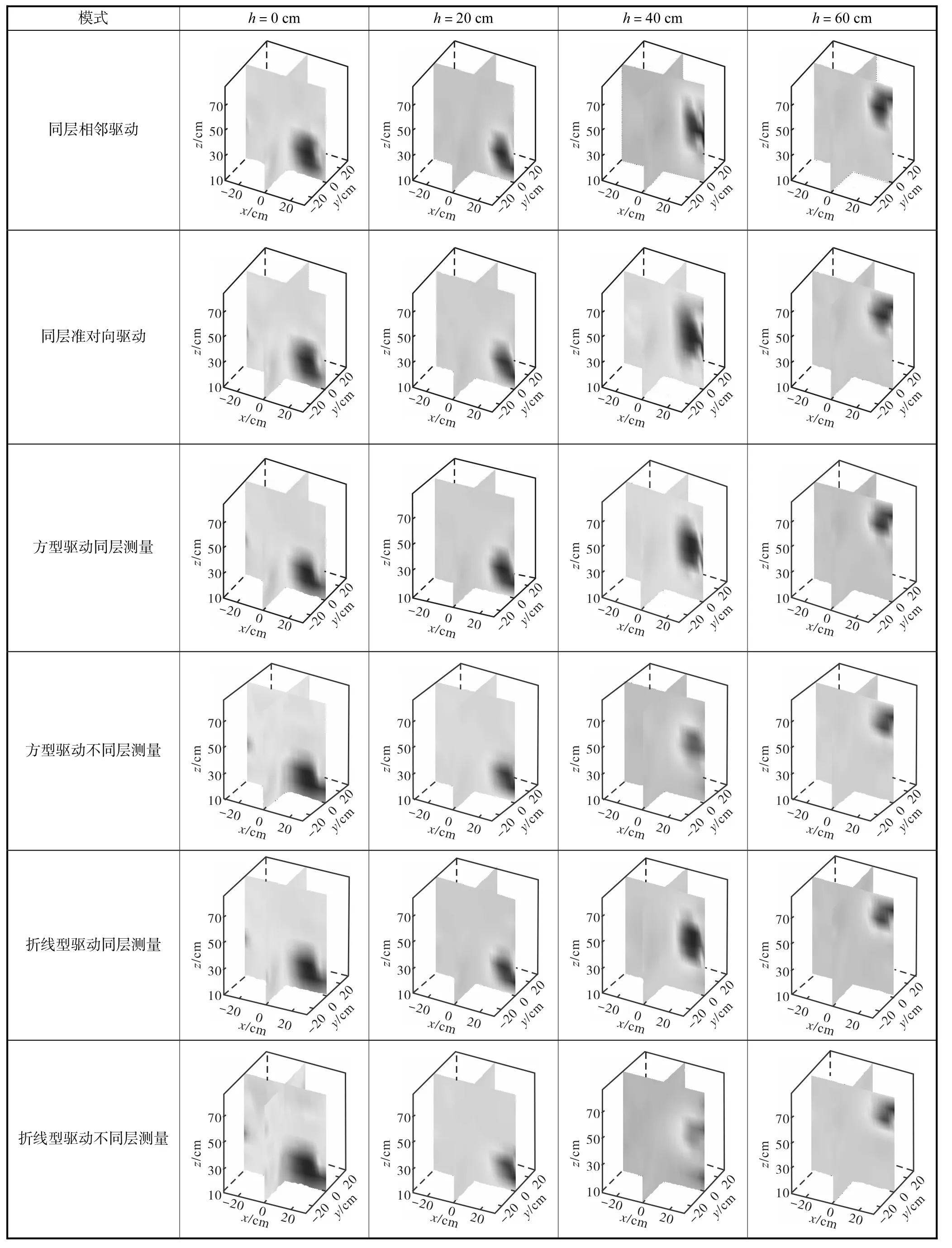
表4 垂直运动实验中6种模式的重建图像Tab.4 Reconstruction images of six patterns in the vertical position experiment

3 结 论

(1) 对于具有双层电极结构的三维EIT系统，相对于不同层测量模式，同层测量模式的成像质量较好.

(2) 对于具有双层电极结构的三维 EIT系统，本文设计和采用了 6种激励/测量模式的组合．结果显示，几种组合各有优缺点，考虑到既要易于测量且成像质量高，同层准对向驱动(同层测量)优于其他几种组合．

［1］van Genderingen H R，van Vught A J，Jansen Jos R C.Regional lung volume during high-frequency oscillatory ventilation by electrical impedance tomography [J].Critical Care Medicine，2004，32(3)：787-794.

［2］Hoetink A E，Faes T J C，Marcus J T，et al. Imaging of thoracic blood volume changes during the heart cycle with electrical impedance using a linear spot-electrode array [J].IEEE Trans on Med Imaging，2002，21(6)：653-661.

［3］Erol R A，Cherian P，Smallwood R H，et al. Can electrical impedance tomography be used to detect gastrooesophageal reflux? [J].Physiological Measurement，1996，17(4A)：A141.

［4］Bagshaw A P，Liston A D，Bayford H，et al. Electrical impedance tomography of human brain function using reconstruction algorithms based on the finite element method [J].NeuroImage，2003，20(2)：752-764.

［5］Zou Y，Guo Z. A review of electrical impedance techniques for breast cancer detection [J].Medical Engineering & Physics，2003，25(2)：79-90.

［6］Polydorides N，Lionheart W R B. A Matlab toolkit for three-dimensional electrical impedance tomography：A contribution to the electrical impedance and diffuse optical reconstruction software project [J].Measurement Science and Technology，2002，13(12)：1871-1883.

［7］Graham B M，Adler A. Electrode placement configurations for 3D EIT [J].Physiological Measurement，2007，28(7)：S29.

［8］汪 婧. ECT/ERT双模态阵列电极优化设计及其正问题研究 [D]. 天津：天津大学电气与自动化工程学院，2008.

Wang Jing. Optimum Design of ECT/ERT Dual-Modality Electrode Array and Study on the Forward Problem [D].Tianjin：School of Electrical Engineering and Automation，Tianjin University，2008(in Chinese).

［9］尤富生，董秀珍，史学涛，等. 电阻抗断层成像中临近和对向驱动模式的研究 [J]. 第四军医大学学报，2004，25(1)：88-91.

You Fusheng，Dong Xiuzhen，Shi Xuetao，et al. Research on adjacent and polar driving in electrical impedance tomography [J].J Fourth Mil Med Univ，2004，25(1)：88-91(in Chinese).

［10］Isaacson D. Distinguishability of conductivities by electric current computed tomography [J].IEEE Trans on Med Imaging，1986，5(2)：91-95.