基于混合整数规划的高级计划排程方法研究
李海宁,孙树栋,郭 杰
(西北工业大学 机电学院,西安 710072)
0 引言
目前,国内大型离散制造企业一般采用企业级物料需求计划(MRP)和车间级生产调度(scheduling)的两层计划编制模式。由于MRP是一类粗粒度的需求计划,其忽略了车间实际的制造能力和零部件加工进度等约束,使得车间生产所依赖的数据源头存在不合理性,从而导致车间计划调度、零部件加工、生产准备等一系列生产组织活动陷入被动和混乱。
高级计划排程 (Advanced Planning and Scheduling,APS) 是一种基于供应链管理和约束理论的先进计划与排产工具。Marriott研究了钢铁工业供应链中的APS系统以改进产品质量、产品收益率和设备效率[1];Romero研究了批量化学加工行业中和财务管理有关的计划和排程问题[2]。徐晓芳等对APS的发展历史、功能优势及特点进行了剖析[3];刘海江等将APS与传统的CRP能力需求计划进行了对比,归纳总结了APS相对于传统能力需求计划的特点[4];肖牧山等提出了基于TOC理念和DBR模型的APS系统与ERP集成的解决方案,并给出了APS与ERP集成的潜在问题和可行方案[5]。
从上述APS的应用和研究方面分析,目前APS主要应用于供应链层次,而在企业层次、车间层次的应用较少;国内对APS的研究主要集中在APS的理念、功能和集成等方面,而在APS的模型和算法求解方面的研究甚少。
本文采用混合整数规划(Mixed Integer Programming,MIP)这类精确型的数学建模方法,以订单或生产任务的准时交付为目标,在考虑产品BOM、零件加工顺序约束、机器加工能力、订单提前/拖期等因素的基础上,构建基于MIP的APS数学模型,并采用遗传算法(Genetic Algorithm, GA)进行APS模型求解,最后通过算例验证模型和方法的有效性。
1 基于混合整数规划的APS模型
1.1 APS模型的假设条件
1)一批零件投入加工后,承制机器的加工期间不能中断;
2)机器在某一时刻只能加工一个零件;
3)一批零件在机器上加工需要考虑生产准备时间;
4)零件在机器上的加工时间已知,且为确定值;
5)订单的BOM结构已知,且零件内部的工艺路线依据父子项依次展开。
1.2 参数和变量说明
1)与订单相关的参数和变量
Oi:订单(i=1, 2, !,n),其中:n为订单数量;
Qi:订单Oi包含的最终产品数量;
Pi:订单Oi对应的最终产品;
Nip:Pi包含零部件p的结构数量;
Di:订单Oi的交货期;
Ci:订单Oi的完工时间;
Ti:订单Oi的拖期天数;
Ei:订单Oi的提前天数;
e:订单提前的每天惩罚系数;
t:订单拖期的每天惩罚系数;
A(p):零部件p的所有子项零件集合;
B:无子项的零件集合。
2)与机器相关的参数和变量
Mk:机器(k=1, 2, !,m),其中:m为机器数量;
rk:Mk的准备时间;
Sipk:订单Oi所属零件p在机器Mk上的开工时间;
tipk:订单Oi所属零件p在机器Mk上的加工时间;
Xip_jq_k:订单Oi所属零件p和订单Oj所属零件q都在机器Mk上加工,若p在q之前加工,则Xip_jq_k=1,否则为0。
1.3 基于MIP的APS模型

其中:
1)公式(1)为目标函数,即所有订单的提前/拖期惩罚总成本最小;
2)公式(2)为机器在生产准备完成后才开始加工;
3)公式(3)为产品BOM中父子零件的加工顺序约束,即:父项零件的开工时间不能小于其子项零件的开工时间与其加工时间之和;
4)公式(5)和(6)表示同一机器在某一时刻只能加工一个零件;
5)公式(7)和(8)分别为订单拖期天数和订单提前天数。这里假设机器每天工作时间为8小时,且天数采用四舍五入的取整方式;
6)公式(9)和(10)限定零部件开工时间、订单完工时间、拖期量、提前量均为正数。
2 基于遗传算法的APS模型求解
由于遗传算法所固有的全局搜索与收敛特性,其得到的次优解往往优于传统方法得到的局部极值解, 且该算法的搜索效率较高。因此, 本文采用遗传算法对上述APS模型进行求解。
2.1 染色体编码与解码操作
1)基于随机键的编码方法
为了表示不同零件的先后加工顺序和增加染色体的多样性,采用文献[6]提出的随机键编码方式。对于n个待加工零件而言,其对应的染色体的码长为n,每个零件对应一个0-1之间的小数。这些小数可以看作一组有序的键值,键值越小,则表示零件加工的优先级越高。例如:若n=5,则(0.1576, 0.9706, 0.9572, 0.4854, 0.8003)就表示一个染色体。
2)染色体解码方法
对于尚未加工且无子项零件的零部件,或者具有子项零件且其子项零件已经加工完成的零部件,形成一个待加工的零部件集合。依据染色体中各基因位的键值大小进行排序,优先安排键值较小的零部件优先开工,而零部件的开工时间则取值为它的所有子项零件中的最晚完工时间和机器最早可加工时间的较大值。
2.2 适应度函数
为避免遗传算法的早熟和随机漫游现象,需要对目标函数值进行适当放大或缩小来获得适应度值。在上述APS模型中,目标函数是最小化提前/拖期总惩罚成本,因此,适应度函数确定为:f'=a/f,其中a取值为0.5。
2.3 基于轮盘赌的选择操作
采用文献[7]提出的基于轮盘赌的比例选择法,以促使适应度值较高的染色体以较大概率被选择到下一代;为了提高遗传算法的优化效果和收敛性,采用精英保留策略[7],以确保当前种群中最好的染色体直接参与下一代种群的遗传操作。
2.4 两点交叉操作
采用如下的两点交叉操作方法。图1为两点交叉操作的示意图,其中交叉概率设为0.6。
1)随机两两配对生成N/2对染色体,其中N为种群规模;
2)从N/2对染色体中随机选取一对染色体(P1,P2)作为父代个体;
3)依据随机键编码方法重新产生一个染色体,确定其小于交叉概率Pc的基因位,互换染色体对(P1,P2)中相应的基因位,生成临时染色体对(T1, T2)。
4)计算临时染色体T1和T2的个体适应度值,分别与父代染色体P1和P2的个体适应度值进行比较,保留适应度值较小的两个染色体作为交叉之后的子代个体。

图1 染色体交叉操作示意图
2.5 变异操作
变异操作方法为:设变异概率为pm,对种群中的任一染色体Vi(i=1, 2, !,N),随机产生(0, 1)内的实数r,若r<pm,则依据随机键编码方法重新产生一个新染色体Vi'来替换Vi,否则,依次对下一染色体执行上述操作。
3 算例仿真
3.1 APS算例
考虑到APS算例的代表性和通用性,本文构造了如图2所示的具有四级装配关系的APS算例。在图2中:既有最终产品F1和F2,同时也包含多个公用零部件,弧线上的数字表示子项零部件的结构数量;另外,部件S4内的零件C13包含两道加工工序(P1, P2),这里将这两道工序视为具有先后加工顺序的两个子零件,即C13P1和C13P2。
表1为包含最终产品F1和F2、部件S1、公用零件C2和C3的5个订单信息,表2为各机器的加工准备时间,表3为各零件、部件和最终产品所需的加工机器及其加工时间(单位:小时)。算例中5台机器的加工能力为8h/天,订单的提前惩罚系数为50元/天,订单的拖期惩罚系数为250元/天。

表1 订单信息

表2 各机器的准备时间

表3 零件的承制机器和加工时间
3.2 仿真结果
遗传算法参数设置为:种群规模为50,进化代数1000次,交叉概率0.6,变异概率0.1,算法终止条件为进化代数。表4为各订单交货期的计算结果,图3、图4分别为目标值收敛曲线和APS算例甘特图。图4中各块上的符号表示某一订单内的零件编号,如“O1S3C2”表示订单O1内组合件S3下的C2零件。

图2 产品结构图
从表3和图4中可以看出:5个订单中,只有订单O2提前一天完工,其他4个订单都是准时完工,因此,APS的目标函数值(即:提前/拖期总惩罚成本)为50元。另外,从图3得知,算法在迭代到158代时达到最优目标值。
4 结论
本文针对高级计划排程问题,以订单的提前/拖期总惩罚成本最小为目标函数,构建了包含BOM结构、零件加工次序、机器能力约束等的APS混合整数规划模型;采用遗传算法对APS模型进行求解,该遗传算法采用随机键编码方式、轮盘赌选择方法、两点交叉操作、精英保留策略等方法;最后采用算例验证了APS模型和GA算法的有效性。本文提出的APS建模和求解算法具有一定的通用性,它适用于机械加工企业的生产计划编制,以及带有组合件生产任务的作业车间计划调度。

表4 订单交货期仿真结果
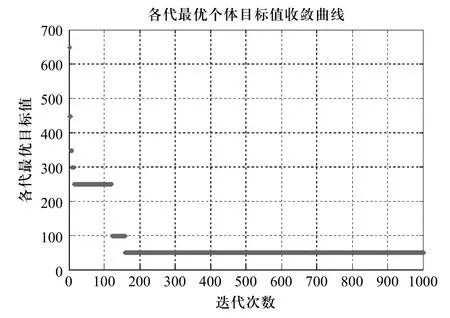
图3 目标值收敛曲线

图4 APS算例仿真结果
[1] Marriott P., et al. Advanced production planning as the core element of a supply chain [J]. MPT Metallurgical Plant and Technology International, 2002, 25(1): 78-82.
[2] Romero J., et al. Integrating Budgeting Models into Scheduling and Planning Models for the Chemical Batch Industry[J]. Industrial and Engineering Chemistry Research, 2003, 42(24): 6125-6134.
[3] 徐晓芳, 张伟, 叶春明. APS剖析[J]. 计算机辅助设计与制造, 2002, (4): 13-17.
[4] 刘海江, 汪进. APS与传统CRP的能力需求分析比较[J].机械设计与制造, 2008, (10): 63-65.
[5] 肖牧山, 鲁砾. 基于APS与ERP集成的新型ERP/APS/MES企业管理系统[J]. 企业技术开发, 2008, (9): 15-18.
[6] Bean J C. Genetic Algorithms and Random Key s for Sequencing and Optimization [J]. ORSA Journal on Computing, 1994, 6(2): 154-159.

