加肋圆柱壳参数化建模与稳定性分析

原晓刚，吴旭光，孟祥尧，冯潇涛

YUAN Xiao-gang，WU Xu-guang，MENG Xiang-yao，FENG Xiao-tao

（西北工业大学 航海学院，西安 710072）

0 引言

为增大壳体内部的容积及减轻壳体结构的重量，鱼雷及水下航行器壳体均采用薄壁结构，同时为了提高壳体抵抗丧失稳定性的能力，在壳体内部都设有加强环肋，因此加肋薄壁结构是鱼雷以及水下航行器壳体的主要形式[1]。

对于耐压壳体除了要考虑其强度外，还应考虑到壳体由于丧失稳定性而导致的壳体破坏。当壳体所承受的外压达到某一临界值时，壳体的变形就不再是稳定的了，当外压继续增加，壳体即开始丧失稳定性，一般在壳体的纵向和周向形成一定数目的凹凸波形，其周向不单是均匀压缩，而且有弯曲变形，变形也不对称与中心轴，随着这种弯曲应力的急剧增长将最终导致壳体的破坏[2]。这种现象称为失稳，又称为屈曲。

由上可知对壳体进行稳定性分析具有十分重要的意义。以往一般通过使用各种理论公式来估算壳体丧失稳定性的临界压力。但壳体失稳问题比较复杂，各种理论计算公式与实际情况在不同程度上都存在一定差异。如今随着计算机技术以及有限元方法的发展，利用一些专业分析软件对建立的壳体模型进行强度和稳定性分析受到了极大的关注[3]。

本文基于ANSYS/APDL进行加肋圆柱壳参数化建模和稳定性分析，省去了大量重复性工作，只要改变不同分析对象的相应参数即可建立分析不同对象的参数化模型并对其进行分析。同时可备以后进行壳体优化设计所用。

1 参数化建模

1.1 加肋圆柱壳参数化模型

进行参数化设计分析首先要建立参数化模型[4]，本文针对薄壁加肋圆柱壳进行建模以及稳定性分析。实际中圆柱壳两端有连接结构，肋板上有安装孔，壳体上还有打压孔等，因此模型较为复杂。为简化有限元模型在保证足够精度下，对壳体结构进行简化，不考虑壳体及肋板上的孔。

根据上述简化，加肋圆柱壳的设计参数可以定为壳体总长L，壳体厚度t，壳体内径R以及内部加强环肋的相关参数。肋骨的参数包括肋骨间距dL和肋骨形式，常用的肋骨形式包括矩形、Z形、I形、T形和U形。不同的肋骨需要有不同的参数，以Z形肋骨为例，需要六个参数W1、W2、W3、t1、t2、t3。具体纵截面图如图1所示。其他类型的肋骨其参数均不超过6个。

1.2 参数化有限元模型的建立

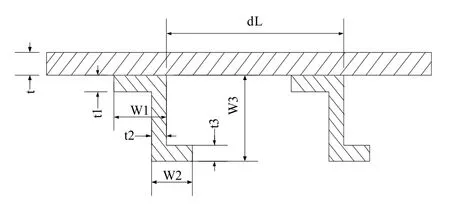
图1 圆柱壳纵截面图

有限元模型建立的好坏直接影响问题分析的准确性，同时为节省计算时间和工作量，有限元模型应尽量简单。由于本文研究的加肋圆柱壳其壁厚均小于典型整体结构尺寸的1/10，因此可以使用壳单元进行模拟。本文选用壳单元和梁单元组合建模的方法，壳体使用壳单元shell93，肋骨使用梁单元beam189，这不仅有利于简化模型，还可以节省计算时间，并且精度足够甚至比用实体单元划分的有限元模型精度更高。

由于使用梁壳单元组合建模，因此壳体用曲面表示而肋骨用曲线表示，壳体厚度与肋骨的截面形式都在单元的相关参数中进行设置。

建立模型时，根据肋骨间距及壳体半径画出连续分段的圆柱体，然后将不需要的体、面、线以及关键点删除，剩余圆柱面与圆柱面之间的圆建立壳体模型。分别赋予不用的结构单元与实常数。由于肋骨与壳板公用关键点，自然而然的耦合在一起。

划分网格时，通过映射方法划分。所得有限元模型如图2所示。当显示实体结构时如图3所示。

图2 有限元模型图

图3 显示实体时的有限元模型剖分图

2 稳定性分析

本文通过使用ANSYS中的屈曲分析来分析壳体的稳定性。屈曲分析分为特征值屈曲分析与非线性屈曲分析。特征值屈曲分析所得结果是理论值结果，而非线性屈曲分析则更贴近实际情况，但相对也比较复杂。在工程计算中使用非线性屈曲分析更贴近实际，也更有应用价值。

2.1 理论计算公式

对于承受均匀内压和外压作用的圆柱形壳体的稳定性计算，国内外的学者进行过大量的理论研究，得到许多不同形式的理论公式预测临界压力，在实际应用中为使用方便一般使用相关公式的简化形式。

我们使用以下根据弹性失稳理论用能量法推导得出的公式来计算理论临界压力，总体失稳的理论临界压力为[2]：

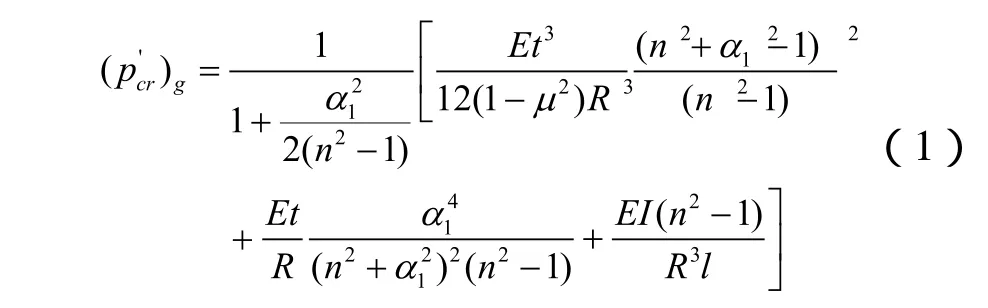
上式中理论临界压力由三个部分组成，在实际应用时，由于壳板的抗弯刚度较肋骨的抗弯刚度小得多，可以忽略第一部分。上式中a1＝pR/L，L为壳体总长；I为肋骨及壳板（一个间距的壳板）的截面惯性矩；n为周向波数，可取2，3，4…，使（p'cr）g为最小值的波数即使总体失稳的波数。

上面公式计算出的是理论临界压力，与实际情况中的临界压力存在一定的差异，一般都比实际值大。因此实际工程应用时，往往要对其进行修正。修正时一般考虑两方面的因素：实际加工中壳体存在的初始形状误差；材料物理特性方面的因素对稳定性的影响。初始缺陷通常使用h1来修正，h1是根据实验和实践经验确定的，一般取h1＝0.75；材料特性对稳定性的影响用h2修正，具体取值可以根据文献[2]确定。由此可得到实际临界压力

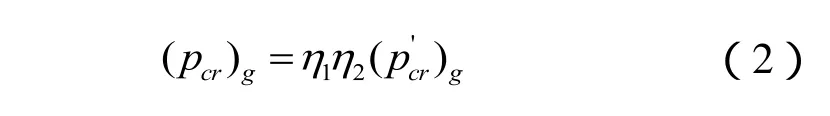
2.2 ANSYS参数化分析过程

使用ANSYS中的APDL参数化语言对加肋圆柱壳进行屈曲分析，大体步骤如下[5]：

1）建立模型划分网格。定义单元类型、单元实常数、材料性质，然后按前述参数化有限元模型的建立过程即可得到有限元模型。

2）施加边界条件和载荷。由于壳体两端连接环的尺寸比内部的肋尺寸大得多，故考虑到其对强度的影响，自由度约束为加肋圆柱壳段两端采用全约束。载荷通过在圆柱壳外表面加表面压力来模拟水中的静压力。在加载自由度约束和表面载荷时，使用选择对象的方式进行加载，并且均是通过坐标位置进行选择。这样的加载方式有利于参数化的分析过程，只要有模型的相关尺寸即可进行载荷的自动的加载。

3）静力分析。此步骤与其它的静力分析基本一致，特别的是需要激活预应力选项（PSTRES），为后续的屈曲分析做准备。此步之后可以通过后处理得到相应的结果。

4）特征值屈曲分析。在静力分析的基础上，重新进入求解器，在求解器中定义分析类型为“Eigen Buckling”（即特征值屈曲分析）。特征值的提取方法选择Block Lanczos法（分块的兰索斯法），其计算速度较快。然后设定模态扩展，因为如果要观察屈曲的变形结果，就必须对结果进行扩展。在扩展模态的对话框中通常选1，即提取第一阶特征值。在此如有需要还可定义载荷步选项，在特征值屈曲分析中有效的载荷步选项是扩展过程选项和输出控制，输出中可以包括扩展的模态形状，也可以包含每一阶模态的相关应力分布。最后求解即可。

5）施加几何初始缺陷或初始扰动。本文通过将特征值屈曲分析后的载荷放大10%～20%来模拟初始扰动。另外也可使用UPCOORD和UPGEOM命令来施加初始几何缺陷。

6）非线性屈曲分析。分析类型选静力分析，但要激活大变形效果（NLGEOM），然后施加放大后的载荷；使用弧长法进行分析，并根据需要设置弧长法停止的条件；还需要定义荷载步并打开自动时间步以利于收敛，定义子步数。之后求解即可。

7）后处理。在计算结束后，可以通过在POST26中进行相关操作得到节点的载荷位移曲线。还可以在POST1中查看失稳时的形变和应力分布。

根据上述过程使用APDL语言编制程序，即可自动运行得到相关结果。对于结构参数不同的加肋圆柱壳可以通过修改程序中的变量得到相应的结果。

2.3 实例验证

为验证使用上述方法所得到的结果的可靠性，取几种不同的加肋圆柱壳进行分析，并将结果与使用理论计算公式所得的结果进行比较。

取某加肋圆柱壳，其总长为1703mm，半径均取267.2mm，壳体材料的弹性模量为0.71× 1011MPa。取以下两种模型进行分析计算：

1）Z形肋骨，肋骨间距120mm。

2）Z形肋骨，肋骨间距187mm。

壳体的其他结构尺寸如图4所示。

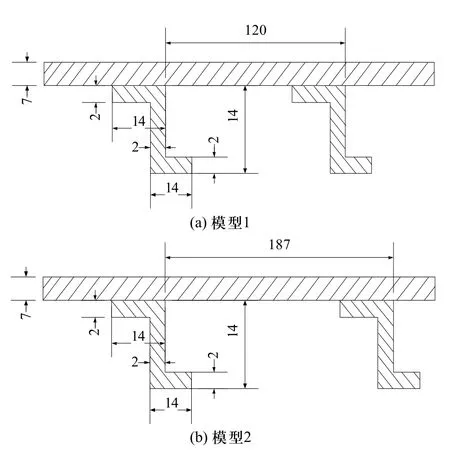
图4 两种模型的具体尺寸

根据公式（2）可得理论计算结果。

使用ANSYS/APDL进行分析后，根据图5中的极值点以及特征值屈曲分析得到的临界压力可得到实际临界压力。各模型具体结果如表1所示。

表1 理论公式结果与ANSYS结果对比

从表1的结果中可以看出，通过ANSYS进行非线性屈曲分析所得到的结果与理论计算的结果十分接近，误差较小，验证了本文所使用的稳定性分析方法，具有一定的实际应用价值。非线性屈曲分析过程完全通过APDL语言控制，适用于实际应用中不同参数的加肋圆柱壳。通过实例对比验证了此方法的正确性，证明具有一定的使用价值。

图5 模型1的载荷位移曲线

[1]贾锐，石秀华，徐宇明，等.基于ANSYS的圆柱薄壳结构模态分析[J].弹箭与制导学报，2008，28（6）：314-316.JIA Rui，SHI Xiuhua，XU Yuming.Model Analysis on Cylindrical Filmy Shell Structure Based on ANSYS[J].Journal of Projectiles，Rockets，Missiles and Guidance，2008,28（6）：314-316.（in Chinese）

[2]张宇文.鱼雷总体设计原理与方法[M].西安：西北工业大学出版社，1998.

[3]郭军，蒋忠亮，秦晓辉，等.基于强度和稳定性的鱼雷壳体可靠性设计[J].鱼雷技术，2011，19（6）：401-405.GUO Jun，JIANG Zhong-liang，QIN Xiao-hui.Reliability Analysis of Torpedo Shell Based on Strength and Stabilty[J].Torpedo Technology，2011，19（6）：401-405.（in Chinese）

[4]何惠江，李楠.基于APDL的鱼雷壳体结构参数化建模[J].鱼雷技术，2010，18（4）：246-248.HE Hui-jiang，LI Nan.Parametric Modeling of Torpedo Shell Structure Based on APDL[J].Torpedo Technology，2010，18（4）：246-248.（in Chinese）

[5]蒋凤昌，朱慈勉，薛剑胜，等._形框架对初始缺陷敏感性的非线性屈曲分析[J].建筑科学，2007，23（5）：11-14.JIANG Feng-chang，ZHU Ci-mian，XUE Jian-sheng.Nonlinear Bucking Analysis of the _-shaped Frame for Initial Sensitivity[J].Building Science，2007，23（5）：11-14.（in Chinese）