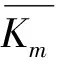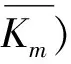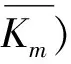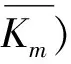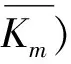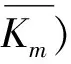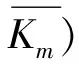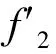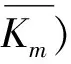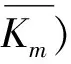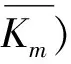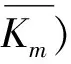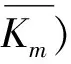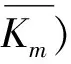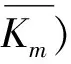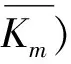非连通图(P3∨∪G及(C3∨∪G的优美性*
王 涛,王 清,李德明
(1.华北科技学院基础部,河北 三河 065201;2.首都师范大学数学系,北京 100048)
图的优美标号问题起源于20世纪60年代,自它问世以来,一直是组合数学的一个热门课题,它在数学理论及实际应用领域都有其重要的研究价值,如运用优美标号来解决完全图分解为同构子图的问题,纠错码设计、通讯网络、雷达脉冲、导弹控制码设计等等[1]。在图的优美性的研究成果中,多数是关于连通图优美性的研究[2-7],近年来,人们开始关注非连通图优美性问题,并取得不少关于此条件下的优美性的结论[8-12]。
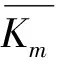
定义1 设图G=(V,E),k为任意正整数,如果存在一个单射f:V→{0,1,…,|E|+k-1},使得对所有的边uv∈E,由f′(uv)=|f(u)-f(v)|导出一个双射f′:E→{k,k+1,…,|E|+k-1},则称图G是k-优美图,f是G的一个k-优美标号。1-优美图也称优美图,1-优美标号也称优美标号。
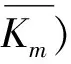
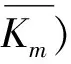
1 A~B优美图
定义2 设图G=(V,E),对数集A和B,其中|B|=|E(G)|,如果存在一个单射f:V→A,使得对所有的边uv∈E,由f′(uv)=|f(u)-f(v)|导出一个双射f′:E→B,则称图G是A~B优美图,f是G的一个A~B优美标号。
由上述定义易知,当A={0,1,…,|E|+k-1},B={k,k+1,…,|E|+k-1}时,A~B优美图即为k-优美图。



f(xjp)=2m+jnt-n+p+j+i-1,(j=1,2,…,k-1,p=1,2,…,n);
f(xkp)=2m+knt+p+k+i-1,(p=1,2,…,n);
f(yjp)=m+j+(p-1)n,(j=1,2,…,k-1,p=1,2,…,t);f(ykp)=m+k+pn,(p=1,2,…,t)

(i)注意到,当k≤n时,m+k+n(l-2)=f(yk,l-2) m+1=f(y1,1) f(y1,2) f(y1,3) f(y1,t) f(yk,t) f(x2,1) f(xk-1,2)<… f(xk,1) 故映射f:V→A是单射。 (ii)对所有的边uv∈E,设f′(uv)=|f(u)-f(v)|,则顶点为{xj1,xj2,…,xjn}和{yj1,yj2,…,yjt}的二部图,由f′导出的边标号集Ej为: Ej=[m+(j-1)nt+i,m+jnt+i-1] 所以f′:E→B是双射。 以下我们用a,b分别是序列x1,x2,…,xn奇数项和偶数项的最大脚标。 定理2 对正整数集A=[m+1,3m+k(n-1)+i]-{2m+k(n-1)+i}, f(x1,p))= (i)当n≥2时,f(x2,2)<2m+2n+i-2;当n<2m+1时,f(x2,a) m+1=f(x2,1) f(x2,a) f(x1,a) f(x2,2)<2m+2n+i-2 f(x1,b-2)<… 故映射f:V→A是单射。 所以f′:E→B是双射。 定理3 设正整数集Ai=[m+1,3m+n-1+t+i]-{2m+n-1+t+i},Bi=[m+i,m+n-2+t+i],(i=1,2),对任意正整数m,n,t,有 (i)当2≤n<2m+1时,图Pn∪St(t)是A1~B1优美图。 (ii)当2≤n≤2m+1时,图Pn∪St(t)是A2~B2优美图。 证明设路Pn的顶点为{x1,x2,…,xn},星St(t)的顶点为{y0;y1,y2,…,yt},V=V(Pn∪St(t)),E=E(Pn∪St(t)),则|E|=|B|=t+n-1。 我们定义图Pn∪St(t)的顶点标号fi如下: , 类似定理1可以证明fi是Pn∪St(t)的一个Ai~Bi优美标号。 当i=2,m=10,n=9,t=6时,非连通图P9∪St(6)的A~B优美标号,可参见下文的图3。 定理4 设图Gi=(V,E),数集Ai=[m+1,3m+|E|+i]-{2m+|E|+i},Bi=[m+i,m+|E|+i-1](i=1,2),若图Gi是Ai~Bi优美图,则 f1(z1)=2m+1+|E|,f1(z2)=0, f1(z3)=3m+2+|E|,f1(uk)=k(k=1,2,…,m) f(v)=f2(v),v∈G1 f1(v1)=2m+2+|E|,f1(v2)=0,f1(v3)=3m+3+|E|,f1(uk)=k(k=1,2,…,m) 结合定理1-3,可得以下结论: 推论1 对任意正整数k,m,n,t,如果满足k≤n≤t,n+k-1≤m,则 图1 (P3∨∪的优美标号 推论2 对任意正整数m,n,t,如果2≤n<2m+1,则 图2 (C3∨∪的优美标号 参考文献: [1]马克杰.优美图[M].北京:北京大学出版社,1991. [2]CHENG H,YAO B,CHEN X,et al.On graceful generalized spiders and caterpillars [J].Ars Combin,2008,87:181-191. [3]YANG Y S,RONG Q,XU X R.A class of graceful graphs [J].Math Research and Exposition,2004,24:520-524. [6]YOUSSEF M Z.On Skolem-graceful and cordial graphs [J].Ars Combin,2006,78:167-177. [7]刘家保,潘向峰.轮形图和扇型图的优美性[J].安徽大学学报:自然科学版,2009,33(4):11-13. [8]刘瑞芹,张昆龙.非连通并图的优美标号研究[J].合肥工业大学学报:自然科学版,2009,32(6):940-944. [9]魏丽侠,贾治中.非连通图G1∪G2及G1∪G2∪K2的优美性[J].应用数学学报,2005,28(4):689-694. [11]王 涛,刘海生,李德明.和轮相关图的优美性[J].中山大学学报:自然科学版,2011,50(6) :16-19.

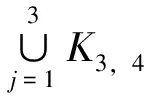
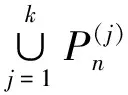
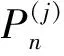
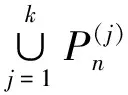

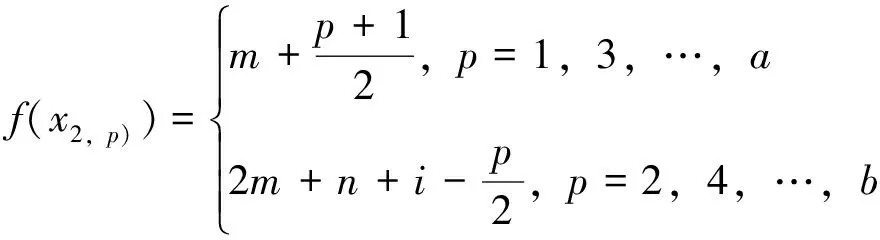


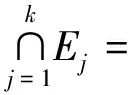

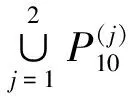
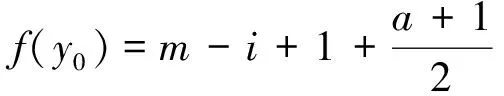

2 非连通图(C3∨∪G及(P3∨∪G的优美性