一种N维数据块正交调制及其解调识别方法的研究*

杨发权,李 赞,罗中良,李红艳,赫本建，高 锐

(1.西安电子科技大学 综合业务网理论及关键技术国家重点实验室,陕西 西安 710071；2.佛山科技学院电子与信息工程学院，广东 佛山 528000；3.惠州学院电子科学系，广东 惠州 516007)

普通正交调制(general orthogonal modulations)简称GOM，主要包括4QAM、16QAM、64QAM、256QAM等类型，在数字调制技术中频带利用率很高、调制方式非常灵活，已广泛应用于各种数字信号的传输领域，如数字卫星电视、数字电视、高速数据传输等领域，因而GOM及其调制识别方法在很多期刊杂志均有介绍[1]。而本文论述的N维数据块正交调制目前在国内外期刊杂志中介绍得很少，并且N维数据块正交调制和GOM比较，频带利用率更高，因此在频带资源有限情况下对N维数据块正交调制及其调制识别方法的研究更有实际意义[2]。

对于GOM信号的识别，需要从估测到的传输信号中提取特征信息，重建信号框架，由于GOM调制维数不高，需要的矢量数不多，因而采用星座图聚类特征识别分类和粒子群与减法聚类提取特征识别分类方法，效果较好，重建信号算法简单[3]，但对N维数据块正交调制，信号框架有2N个矢量，并且矢量数按指数方式增加，信号重建算法较复杂[4]，为此本文提出提取基本矢量的一种新方法，对于N维数据块正交调制信号，基本矢量由N+1个矢量组成，信号重建需要的矢量数、基本矢量数如下表1所示。

表1 信号重建需要的矢量数、基本矢量数

从表1中知当维数较大时，基本矢量数比矢量数小很多，因此采用基本矢量进行信号重建以达到解调识别目的，则计算复杂程度相比较要简单很多。

1 N维数据块正交调制模型

N维数据块正交调制与GOM比较，GOM仅有两路信号进行正交调制叠加后传输，而N维数据块正交调制则是有N路数据(称N维数据块)分别与N个同频正交载波调制叠加后传输。随着维数N增大，对于N维数据块正交调制信号模型的数学描述比较困难，为此本文中的N维数据块正交调制可通过多维转动中的转换矩阵来表示,调制参数包括转动面和转动角度两个物理量[5]。一个N维的信息矢量S可表示为：S=[S1,S2,…,Sn,…SN]，对于Q进制Sn=±d,±3d,…,±(Q-1)d,n∈(1,2,…N),一个N维的数据块调制信号矢量C=[C1,C2,…,CN]可定义为

C=SH

(1)

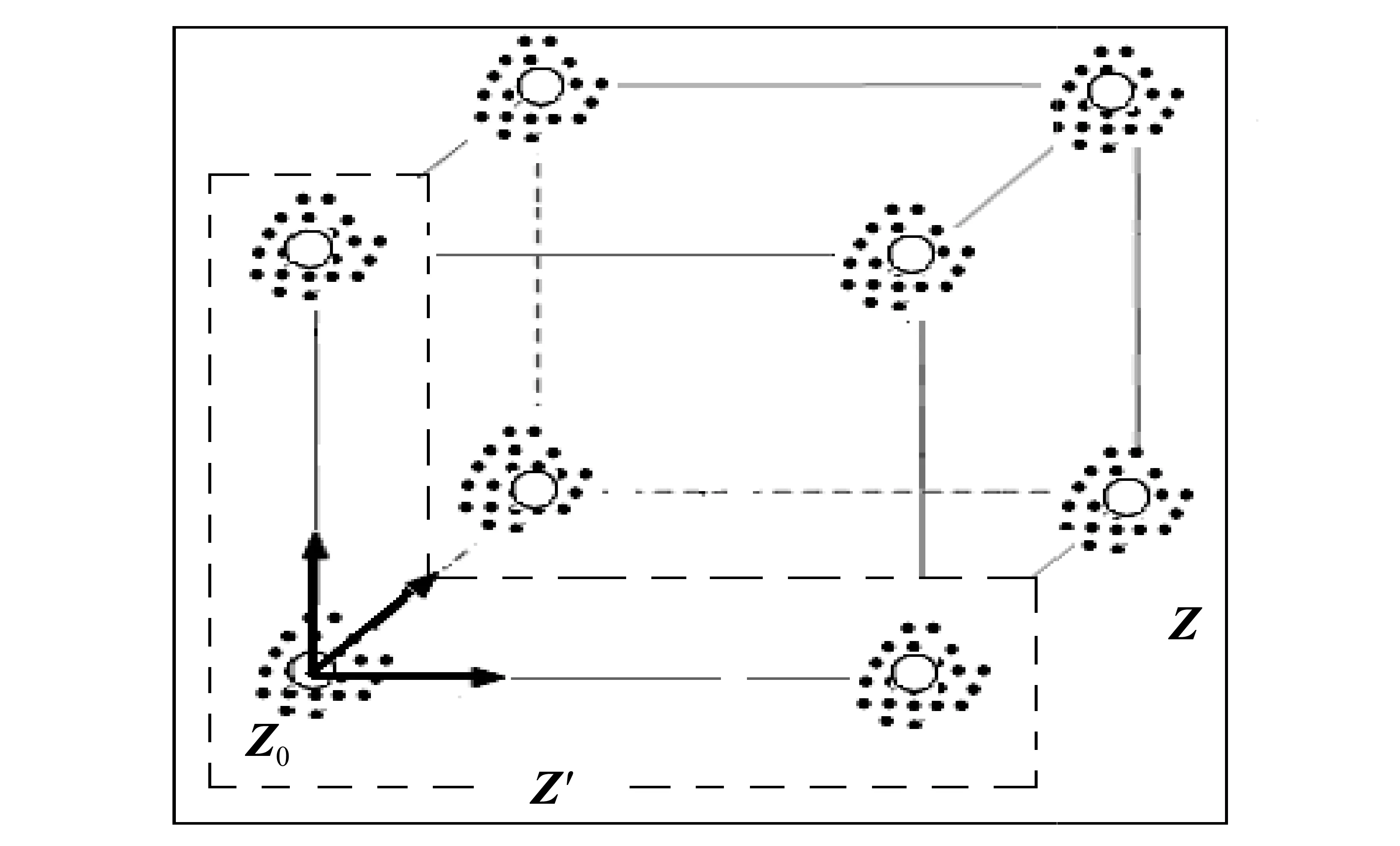
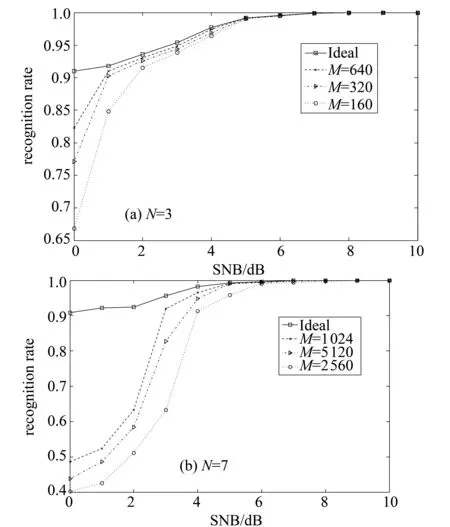
其中H是转换矩阵，它包括在多维空间连续转动信息，而多维空间的转动可通过转动矩阵R和转换矩阵H的内积来表示。定义在第i维与第j维之间的转动角用θij表示，设i

(2)

式中rii=rjj=cosα,rij=-rji=-sinα,rkk=1(k≠i,j),rkl=0(k≠l)

当经L次连续转动到时，转换矩阵可表示为

H=RLRL-1R…RM…R2R1E

(3)

其中RM表示从第iM维到第jM维的转动矩阵，因此对于N维数据块正交调制可通过改变调制参数即改变转动面和转动角度来表示。对于三维数据块正交调制，设信息符号为二进制数据即Q=2 ，取Sn=±1 根据以上定义可得到其星座图如图1所示，图中传输和接收的信号分别用白色的小园圈和黑色点表示。

图1 三维数据调制信号星座图

2 N维数据块正交调制解调识别原理

文中N维数据块正交调制解调识别原理方框图如图2所示。

图2 解调识别原理方框图

发射机输出的数据块正交调制信号在信道中受到高斯白噪声干扰，在接收端，所有接收信号用来重建N维信号框架(聚类样品)，再通过基本矢量估计和提取，分2路：一路送数据解调以解调恢复数据，另一路送矩阵转换以达到调制方式的识别目的[6]。

在接收端并不是所有的接收信号都是用来提取基本矢量，定义所有接收信号聚类样品用Z表示，用来提取基本矢量的信号聚类样品叫聚类目标样品用Z′表示，接收信号序列的初始矢量用Z0表示，其它序列信号矢量用Z1，Z2……ZM-1表示，其中M为总的接收信号聚类样品数目。以三维数据块正交调制空间为例，所有接收信号聚类样品Z、聚类目标样品Z′、初始矢量用Z0及另外三个基本矢量如图3所示。

图3 Z、Z′、Z0及另外三个基本矢量图

聚类目标样品Z′的选择很重要，直接影响到基本矢量的提取，从而影响到数据块调制信号的识别[7-8]，下面分别论述聚类目标样品Z′的选择、基本矢量的估计提取算法及调制识别的原理。

设初始矢量Z0与第i维矢量Zi之间夹角为

(4)

其中Z0·Zi为矢量Z0与Zi的内积， ‖Z0‖和‖Zi‖分别为Z0、Zi的模。

定义θne和θop其中：

(5)

(6)

选取θne和θop的平均值作为判断阀值角

(7)

若θi大于θt，则相对相邻的矢量，Zi远离Z0，所以Zi不属于聚类目标样品Z′，只有当θi小于θt时Zi才属于聚类目标样品Z′。

聚类目标样品Z′集聚成N+1组，每组的中心矢量分别用c1,c2,…,cN+1表示，N+1个矢量中最靠近初始矢量Z0的矢量我们称为基本矢量的支点矢量，用cp表示，这样得到估测的基本矢量为

ei=cj-cp

(8)

其中j= 1,2,…,N+1,cj≠cp,估测到的基本矢量的性能与初始矢量Z0的选择有关，为了提高基本矢量的估测性能，我们用cp代替Z0，并且对(4)-(7)式采用迭代法计算处理[9-11]，最终提取到符合要求的基本矢量。

3 N维数据块正交调制解调识别性能理论分析

N维数据块正交调制识别性能可用识别率高低表示。

设N维的数据块调制信号传输矢量为

T=[T1,T2,…Tn…,TN]

(9)

其中：

Tn=md=±d,±3d,…,±(Q-1)d,

n∈(1,2,…N)

噪声矢量为：N=[N1,N2,…,NN]

若接收信号总矢量为：Y=[Y1,Y2,…,YN]，则接收信号总矢量为

Y=T+N

(10)

在接收端，信号的识别率p由接收信号矢量Y在提取的基本矢量(设为Z1)上的投影y1来决定，则在发送N维的数据块调制信号T1=md时，理论上识别率为：y1处于(m-1)d与(m+1)d之间的概率[12-13],即

p=proble[(m-1)d

(11)

定义：(m-1)d与(m+1)d之间范围用L表示，考虑噪声对接收信号和提取的基本矢量的影响，信号的识别率应该由用转动矩阵R对接收信号进行变换后再在无误差的基本矢量轴(设为X轴)上的投影分量来决定[14]。而该投影分量为

y1X=R(T+N)·(1,0,…,0)=

(RT+RN)·(1,0,…,0)=f(θ)+n1

(12)

其中：f(θ)=RZ·(1,0,…,0)，θ=(…,θij,…)，n1是一维均值为0，方差为σ2高斯白噪声，因此理论上在发送N维的数据块调制信号T1=md时，理想的识别率为

(13)

4 仿真结果及其性能分析

我们用本文提出的算法对N维数据块正交调制信号的识别用MATLAB做仿真实验。仿真参数及条件为:载波频率fc=150 kHz,采样速率fs=1 200 kHz,符号率RB=12.5 kb/s,ASK的调制系数选为0.8,每个识别样本采用2 048个样点，使用随机序列作为调制信号,实验次数取1 000次，环境为理想加性高斯白噪声信道,信噪比取5～10 dB。

采用基本矢量算法和采用全部接收信号矢量进行调制识别相比较，识别所用的时间与维数之间的关系仿真结果如下表2所示。

表2 计算复杂程度仿真比较

由表2知随着维数的增大，采用基本矢量算法和采用全部接收信号矢量进行调制识别相比较，所用的时间相对越来越少，所以文中采用的算法使数据块调制的解调和识别计算复杂程度大为减低。

对于N维数据块正交调制，由表1知：接收端重建信号样品框架需2N个矢量数，为此取接收聚类样品数目M=80×2N，当N分别取3、4、5、6、7时，对应的聚类样品数目M应分别为640、1 280、2 560、5 120、10 240，在信噪比分别为5 dB、10 dB 时，识别率与迭代次数λ之间关系仿真结果如图5所示。

图5 识别率与迭代次数λ之间关系图

从图5知：①当信噪比为5 dB，迭代次数λ小于4次时，维数N越高识别率越低，这是由于迭代次数不够，基本矢量估计不准确，识别率相对低些，并且随着维数N越高，识别率越来越低。但当迭代次数λ等于4次时，识别率以达到98%以上，当迭代次数λ大于4次时，基本矢量估计提取误差很小并且基本稳定，因此，在N分别取3、4、5、6、7情况下，识别率大体相等并且维持在98%以上。②当信噪比为10 dB时，迭代次数λ小于4次时，和接收信噪比为5 dB情况同理，维数N越高识别率越低，但当迭代次数λ等于3次时，识别率就可以达到99%以上，当迭代次数λ大于4次时，在N分别取3、4、5、6、7情况下，识别率大体相等并且大约等于1。

当维数N分别取3维和7维时，N维数据块正交调制信号的识别率与输入信噪比之间关系如图6所示。

图6 识别率与输入信噪比之间关系

两图比较知：①在接收聚类样品数目M、迭代次数λ、在信噪比相同情况下，维数N=3时的识别率比维数N=7时的识别率高。②在信噪声比大于4 dB时识别率可达到90%以上，其中在N=3维时识别率可达到95%以上；在信噪声比为5 dB，N=3维及信噪声比为6 dB，N=7维时，识别率已非常逼近相对应的理论值并且接近100% ，可见，本文提出的识别方法，性能较好。

5 结 论

文中提出N维数据块正交调制方法，并对其调制解调识别方法进行研究。在普通正交调制基础上，通过从接收信号矢量序列中选择聚类目标样品，采用聚类迭代算法，提取基本矢量，可用于高维正交数据块解调和调制识别，数据块正交调制识别性能即识别率的高低与维数N、接收聚类样品数目M、迭代次数λ、输入信噪比等因素有关，随着接收信号矢量数目的增加，通过聚类迭代，识别率大为提高，并逐渐接近理想状况，当信噪声比为4 dB时识别率可达到90%以上，当信噪声比为6 dB，识别率可达到近100%，同时计算复杂程度和采用全部接收信号矢量识别相比大为减少。

参考文献：

[1]XI J X,WANG Z X.MQAM modulation scheme recognition using Hilbert transform[J].Journal on Communication,2007,28(6):320-325.

[2]KATAYAMA T,OKA I,ATA S.Modulation identification by general orthogonal modulations[C]∥Proceedings of the 2008 International Conference on Advanced Technologies for Communications (ATC 2008),2008:12-15.

[3]乔纪纲.基于像元信息分解的城市绿地信息自动提取系统[J].中山大学学报:自然科学版，2008,47(3):133-136.

[4]YAMAMOTO T,OKA I,ATA S.Clustering and labeling of orthogonal signals for modulation identifications[C]∥Proceedings of the 2008 International Symposium on Information Theory and its Applications(ISITA 2008),2008,65-69.

[5]熊会元，宗志坚,余志，等.基于凸包的棋盘格角点自动识别与定位方法[J].中山大学学报：自然科学版，2009 ，48 (1): 1-5.

[6]侯健,王华奎.一种基于星座图聚类的MQAM识别方法[J].无线电通信技术,2009(3)：35-38.

[7]张广驰,江艳敏,秦家银.OFDM系统中基于有限反馈的余量自适应比特加载[J].中山大学学报：自然科学版,2009,48 (5): 38-41.

[8]OKA I，FOSSORIER M P C.A general othogonal modulation model for software radios[J].IEEE Transaction on Communications,2009,54(10):7-12.

[9]LONG C,CHUGG K,POLYDOROS A.Further results in likelihood classification of QAM signals[J].in Proc IEEE Milcom,2008,94(25):57-61.

[10]罗中良,余剑锋.基于多传感器的神经网络模式识别方法[J].中山大学学报:自然科学版，2001,41(5):21-24.

[11]罗中良,施仁.神经网络用于产品品质鉴定的新方法[J].兰州大学学报，2001,39(4)：55-59.

[12]XU Zhinan1,BAI Wenle.A novel blind recognition algorithm for modulated m-QAM signals[C]∥Communications and Mobile Computing of the 2010 International Conference,2010:461-465.

[13]于志明.无线通信系统中的信号识别技术研究[D].哈尔滨:哈尔滨工程大学，2010.

[14]甘露.通信信号测向与分析技术研究[D].成都：电子科技大学，2009.