基于GIS和多智能体的城市人口分布模拟*

康停军，张新长，赵 元，王海鹰，张 维

(1.中山大学 地理科学与规划学院，广东 广州 510275;2.华南农业大学 信息学院，广东 广州 510642)

人口的增长已经给全球资源、环境承载能力造成了巨大压力；获取高精度的人口空间分布信息对于分析人口、资源、环境和社会经济发展的相互作用机制，提高资源和环境的综合管理能力具有非常重要的意义[1-2]。近年来，人口数据分布网格化成为人口空间分布研究领域的热点，涌现出一系列的研究成果，如遗传算法/遗传规划建模[1]、夜间灯光遥感数据[2]、重力模型[3-4]等一批模型、方法在区域层面得到应用。在城市内部人口分布模拟方面，部分学者开展了基于数字人口模型[5]、核心估计[6]、航空影像[7]等模型及数据的城市人口分布模拟。上述研究多采用“自上而下”的计量数学模型，需要大量的先验知识来建立人口和诸多影响因子之间的数学关系。另外，城市人口分布通常伴随着不同类型居民的居住分异现象，尤其是北京、上海、广州等大城市居住分异现象已比较明显，受到越来越多的研究关注[8-10]。因此，城市居住分异分析已经成为人口分布模拟不可忽略的一部分，但是“自上而下”的计量模型仅能在数量上取得较好的人口分布模拟精度，而无法对城市内部人口分布所表现出的分异特性进行描述。

微观个体(家庭)根据自身的偏好以及环境因素的影响在各居住地块不断进行选择搬迁而呈现宏观的城市人口空间分布，这构成了一个典型的“自下而上”复杂系统。多智能体理论的出现为解决“自下而上”的复杂问题提供了解决方法，其已在土地利用模拟[11]、土地利用规划[12]、居住选择及居住分异[10,13-14]等领域得到了广泛的应用。部分学者进行了基于多智能体的人口格网化分布或增长模拟的尝试研究[15-16]。吴静[15]利用多智能体分析了近2000年中国人口的演变，其理论框架适合于进行大尺度人口分布模拟，而不适用于城市内部人口分布模拟。肖洪[16]利用多智能体对长沙市人口分布进行了模拟和预测，该研究以Clark模型模拟结果对多智能体模拟模型进行初始化和精度检验，适用性受到一定限制。

目前，采用“自下而上”方法研究城市人口分布的成果十分有限。本文通过探讨微观个体与城市外部环境之间的相互作用、智能体之间的互动竞争协商，在多智能体理论框架基础上，构建了基于多智能体的城市人口分布模拟模型(Simulation Model for Urban Population Distribution-SMUPD)。进行了模型应用研究，并对模拟结果进行了检验。

1 城市人口分布模拟模型

1.1 分布影响要素

在大区域尺度人口分布研究方面主要考虑的影响要素包括：区域交通条件、气候、地形及土地利用方式等要素[1-4]。人口在城市内部分布的则主要受交通条件、自然环境、公共服务设施等因素的影响[17]。本文考虑的影响因素包括：居住用地、交通条件、自然环境、公共服务设施、教育环境。

1.1.1 居住用地 所有Agent均在已有居住用地单元进行选择搬迁，不考虑其它用地类型(林地、农田等)转换为居住用地的情况。

1.1.2 自然环境 随着人们的居住观念逐渐转变，居住地周围的自然环境成为需要考虑的一个重要因素，将水体、绿地、林地作为衡量自然环境质量的因子[10]。

(1)

式中，PEnvi表示环境质量，Dwater表示到水体(江、湖泊)的直线距离，λ1为衰减系数，r表示邻域的半径，Num表示邻域中绿地、林地所占的单元数量，ww为水体对环境质量的权重系数，wg为绿地及林地的权重系数。

1.1.3 交通条件 交通的便捷程度是选择居住地需要考虑的一个重要影响因素，本文采用指数衰减函数反映交通的通达度[11]。

PTraf=wr.e-λr·DRoad+ws.e-λs*DSubway+

we.e-λe*DExpressway

(2)

式中，PTraf表示交通的通达度，DRoad、DSubway、DExpressway分别表示到市内道路(包括主干道、次干道)、地铁、高速公路的直线距离；wr、ws、we分别表示上述交通方式的权重系数；λr、λs、λe分为对应的空间衰减系数。

1.1.4 公共服务设施 考虑的公共服务设施包括医院、娱乐设施、公园、商业中心、体育场馆、文化设施、市场商业大厦、金融证券公司，均采用指数衰减函数表达其空间吸引力。

1.1.5 教育环境 对于有入学适龄小孩的家庭而言，寻找优质学区资源成为居住考虑的一个主要因素。鉴于大城市多采取划片招生、就近入学的原则，本文对不同等级(省、市、普通)的学校赋予不同的权重分值，并划定其影响范围。中学影响要素和小学影响要素加权得到教育环境影响要素。

1.2 模型框架及运行机制

模型框架如图(1)所示，主要由多智能体、决策规则、影响要素、居住元胞及GIS系统等各部分有机耦合组成。模型对复杂的智能体(Agent)进行抽象与描述，仅考虑居民Agent，由于居民在城市内部的搬迁行为一般以家庭为单位，因此本文设计的居民Agent以家庭为单位，每个Agent代表一个家庭。

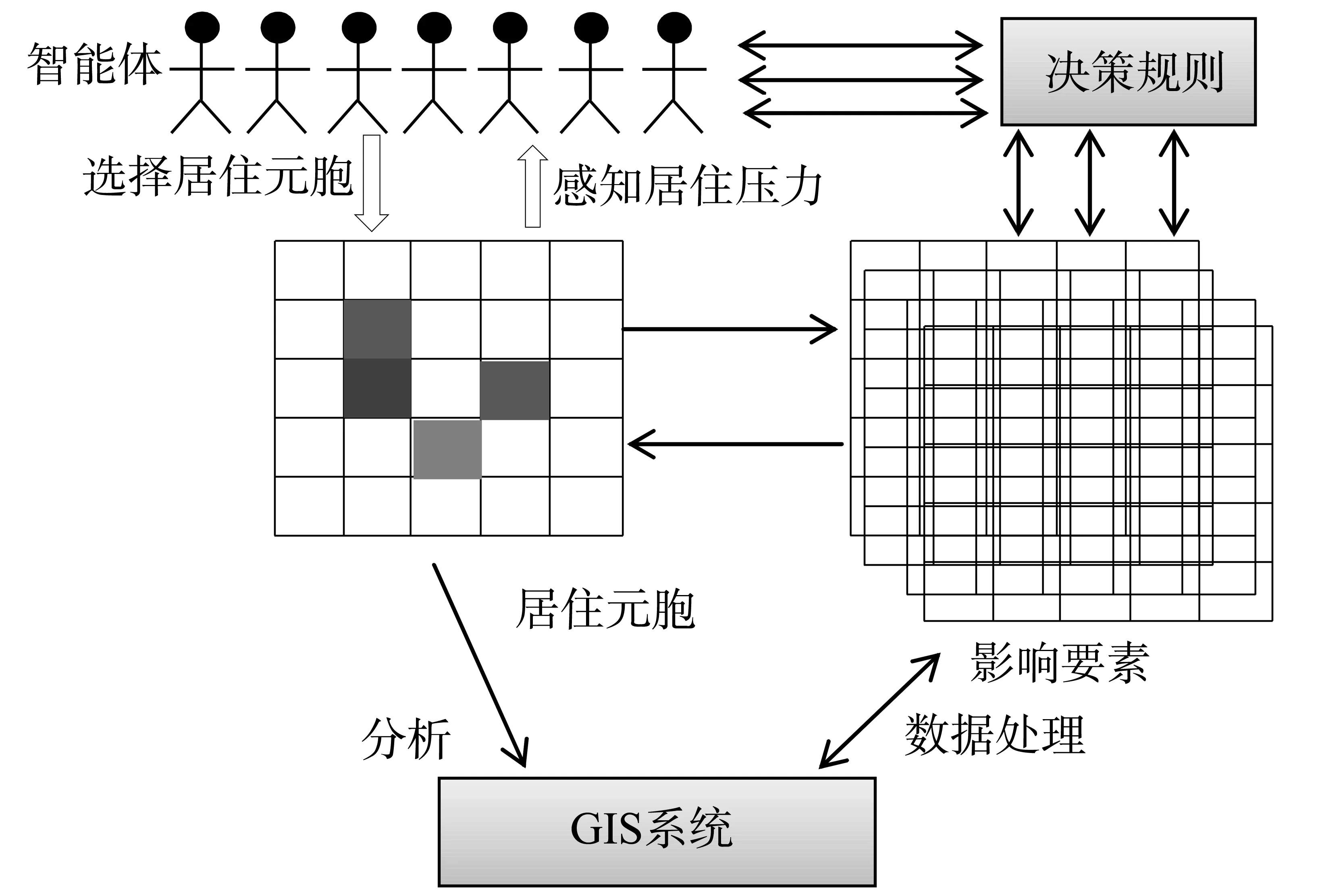
图1 基于多智能体的城市人口分布模拟模型框架

模型运行机制如下：初始状态下，按照城市家庭数量生成Agent，每个居住元胞内包含相同数量的Agents，Agent根据自身经济状况及所在居住元胞的居住压力，做出是否迁居的决策；如果迁居则根据各自的偏好以及环境因素的影响，选择适宜的居住地进行搬迁；如果不搬迁，则继续居住在原居住元胞，通过Agents不断在城市居住空间中进行搬迁，模拟城市人口空间分布。

1.3 Agent决策行为

1.3.1 计算居住压力 Agentm在居住元胞Lxy的居住压力由2部分构成：经济压力、社会压力[14]。m在元胞Lxy所产生的经济压力包含两部分：m的收入与Lxy房屋价格的差异以及m的收入与居住在元胞Lxy所有Agent的平均收入差异。经济压力可以表示为：

PEconomic(m,t,xy)=1-

waverage·|I(m,t,xy)-∑I(,t,xy)/Popxy|) (3)

m在元胞Lxy所产生的社会压力由两部分构成：类型压力、效用压力。类型压力是由居住在元胞Lxy且与m同类型的Agent占Lxy中总Agent的比例决定的，比例越高，该压力越小。效用压力由m在Lxy的效用与相邻区域居住元胞中的效用差异构成。社会压力可以表示为：

PSocial(m,t,xy)=1-(1-wtype·PType(m,t,xy))·(1-wutility·Putility(m,t,xy))

(4a)

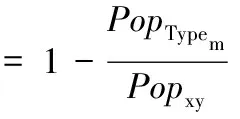
(4b)

(4c)

式(4c)中的U(m,xy)为m在元胞Lxy的效用，可计算如下：

U(m,xy)=wenvi·PEnvi+wtraf·PTraf+

wconvi·PConvi+wedu·PEdu+εxy

(5)

式中，PEnvi、PTraf、PConvi、PEdu为环境、交通通达度、公用设施、教育资源等因素影响值，wenvi、wtraf、wconvi、wedu分别为m对上述影响因素的偏好权重，其总和为1；εxy为随机扰动项。

t时刻m在元胞Lxy所产生的居住压力为：

P(m,t,xy)=wP·PEconomic(m,t,xy)+

(1-wP)·PSocial(m,t,xy)

(6)

式中，wP为属于[0,1]的常数，其它参数含义同上。

1.3.2 选择居住元胞 Agentm在居住压力作用下以一定的概率决定是否进行迁居，决定迁居的概率取决于居住压力，二者呈线性关系[13]，概率为：

PM=P0+(1-P0)·P(m,t,xy)

(7)

式中：PM为迁居概率，P0为属于[0,1]的常数，其它参数含义同上。

只有符合式(8)条件的居住元胞才可以作为Agentm的候选迁居地。

式中，TWLij为m是否将Lij作为其迁居候选地的意愿，U(m,ij)、U(m,xy)为Agentm在迁居目标点和现居住点的区位效用；P(m,t,ij)、P(m,t,xy)为智能体m在迁居目标点和现居住点的居住压力，其它参数意义同上。

利用离散选择模型确定迁居的候选位置，根据McFadden的证明[11,18]，Agentm随机选择位置Lij的概率为：

(9)

1.3.3 搬迁及更新 如果元胞Lij所居住的Agent数量没有达到最大限制，则直接搬迁至Lij。如果已经达到最大限制，则Agentm与居住元胞Lij中的任一Agentn进行协商，协商成功，n开始迁居，如果n搬迁成功，则m搬迁至居住元胞Lij。否则，m迁居失败，返回原居住元胞。协商成功的概率为：

(10)

式中，PConsult表示协商成功的概率，其它参数含义同上。搬迁后智能体更新其归属居住元胞的信息。

1.3.4 智能体经济状态及房屋价格变化 模型运行过程中，智能体的经济状态会随着其所在居住元胞房价的变化而变化。m在t时刻位于居住元胞Lxy的收入为：

(11)

模型运行过程中对房屋价格进行更新，本文假设同一居住元胞内部所有房屋价格是相同的，某一居住元胞房屋价格与该元胞房屋前一时刻的价格、元胞内部所有Agent的收入，以及周边区域中居住元胞房屋价格有关。居住元胞Lxy房价更新为：

(1+α)··

(12)

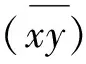
若居住元胞Lxy在t时刻无人居住，其房屋价格会随着时间折旧[13]：

(1-β)·

(13)

式中，β为折旧率，其余参数含义同上式。

2 应用案例实验

2.1 研究区概况及数据

本文的研究区(图2)为广州市2006年所辖的荔湾区(不含原芳村区)、越秀区、天河区、海珠区及白云区的14个行政街道(江高镇、人和镇、太和镇、钟落潭镇4个镇除外)，由于准确获取流动人口数据存在一定难度，本文仅研究城市内部常住人口的分布。

图2 研究区范围示意图

模拟所采用的空间数据均为2006年数据，主要包括：居住地分布图，主干道、次干道及地铁分布图，交通道路图，省、市及普通中小学分布图，银行、公园、医院、市场、商业大厦、餐饮、宾馆、体育设施分布图以及土地价格分布图。人口数据为广州市统计年鉴获取的2006年研究区各街道常住人口家庭数。社会经济统计资料包括《2006年广州统计年鉴》、《2006年广州市国民经济和社会发展统计公报》、《广州市城乡规划管理技术规定》等资料。

公共服务设施的衰减系数由其可达性决定，计算各居住元胞到距其最近公共服务设施的距离，90%的距离应该落入可达性区间[20]，区间上限为均值加标准差。假设在可达性区间的最大值处，可达性的影响值下降了90%。依据此原则，计算了各种公共服务设施及道路、河流、湖泊的可达性区间及衰减系数值(表1)。

统计资料显示，广州家庭平均人口3.21人，城镇居民人均居住面积19.44 m2。按照规划最大容积率3.2进行计算，每公顷内最大住宅数量为3.2×10 000/(3.21×19.44)≈513，因此将513作为每个居住元胞可以容纳Agents数量的最大值。

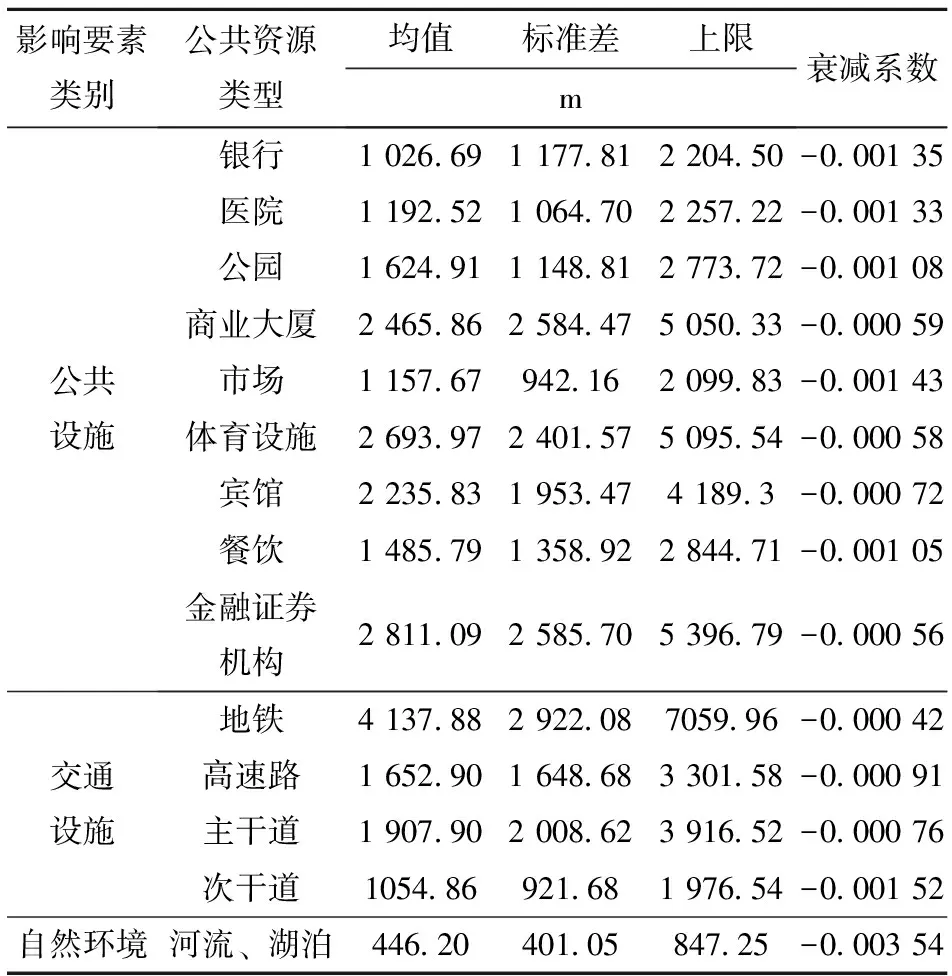
表1 影响因素可达性区间及衰减系数

图3为实验区相关影响因素，其空间分辨率均为100 m×100 m。

图3 居住影响要素

2.2 智能体分类及权重确定

根据实验区2006年统计年鉴及经济年鉴、教育局统计资料，按照家庭月收入状况(小于2 000为低收入、2 000～10 000为中等收入、大于10 000为高收入)以及是否有小学初中适龄小孩将智能体划分为6种类型，各类型比例及数量如表2所示。按照式(12)对智能体的收入进行更新并更新其收入排名，根据排名判断其类型是否发生改变。

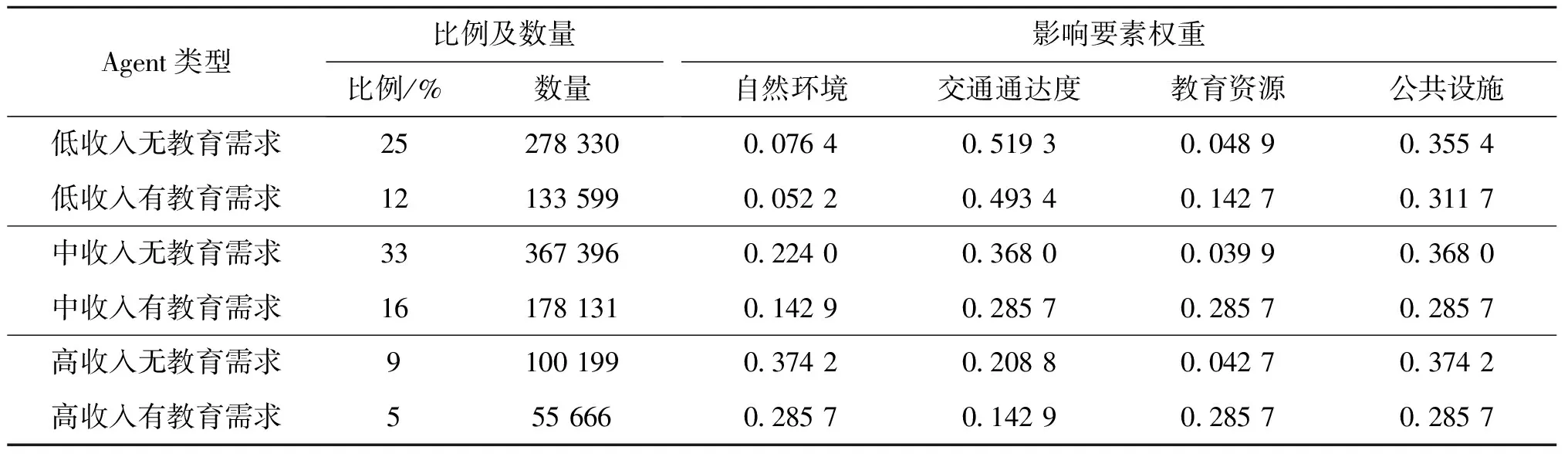
表2 Agent数量及权重

2.3 模拟结果

采用C++编程对模型进行实现。实验区2006年居住元胞数量为9 201，共有家庭数量1 113 321户，初始时按照1∶1的比例生成Agents，每个居住元胞初始Agents数量为121，各居住元胞内Agent的类型均为随机选取。

当P0=0.6,wP=0.8时模型取得较好的模拟效果，经过验证发现，自T=5 000开始，T=5 000、8 000、10 000及12 000各居住元胞Agent数量的相关性高达95%，说明模型已经基本达到均衡稳定的状态。取T=12 000时刻模拟结果作为SMUPD模型模拟的最终结果。T=0，1 000，5 000，12 000时刻模拟结果如图4所示。

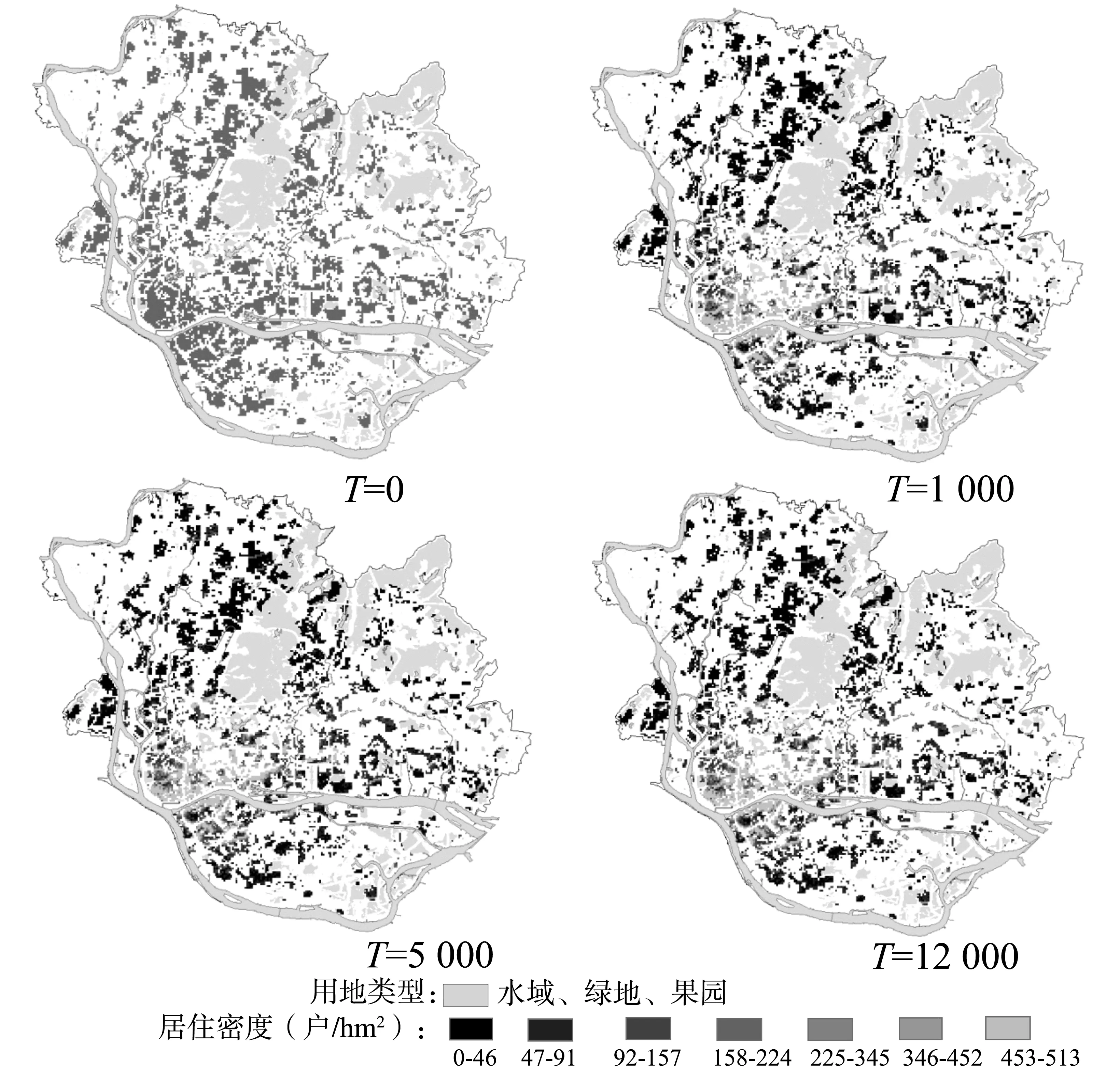
图4 不同时刻居住分布模拟

2.4 结果分析

2.4.1 人口数据空间化精度分析 重力模型已在人口分布研究中得到广泛应用[1,21]，本文采用重力模型对实验区人口分布进行模拟，利用重力模型模拟结果与SMUPD模拟结果进行对比分析。研究区重力模型结构为：

PLxy=1113321·[PEnvi(x,y)]0.28·[PTraf(x,y)]0.55·

[PEdu(x,y)]0.21·[PConvi(x,y)]0.47

(14)

式中,PLxy为元胞Lxy的重力模型模拟值，PEnvi(x,y)、PTraf(x,y)、PEdu(x,y)、PConvi(x,y)分别为环境、交通通达度、教育资源、公共服务设施在居住元胞Lxy的影响值。

结合街道边界将模拟后各居住元胞内的智能体数量累加，与统计年鉴获得的该街道的真实数据进行对比分析，采取比率误差衡量模拟的精度水平：

×100%

(15)

式中，Dm为第m个街道模拟家庭数量与统计调查数据的偏离度，PSimum为第m个街道模拟数据，PStaticm为第m个街道统计调查数据。

在模拟的t时刻各街道离散度之和与街道数量之比为平均偏离度[22]，其公式为：

(16)

式中：DAverT为T时刻模拟的平均偏离度，M为街道数量，平均偏离度越小，模拟精度越高。

重力模型和SMUPD模型模拟结果的比率误差见图(5)、平均偏离度及模拟精度见表(3)。

表3 平均偏离度及模拟精度

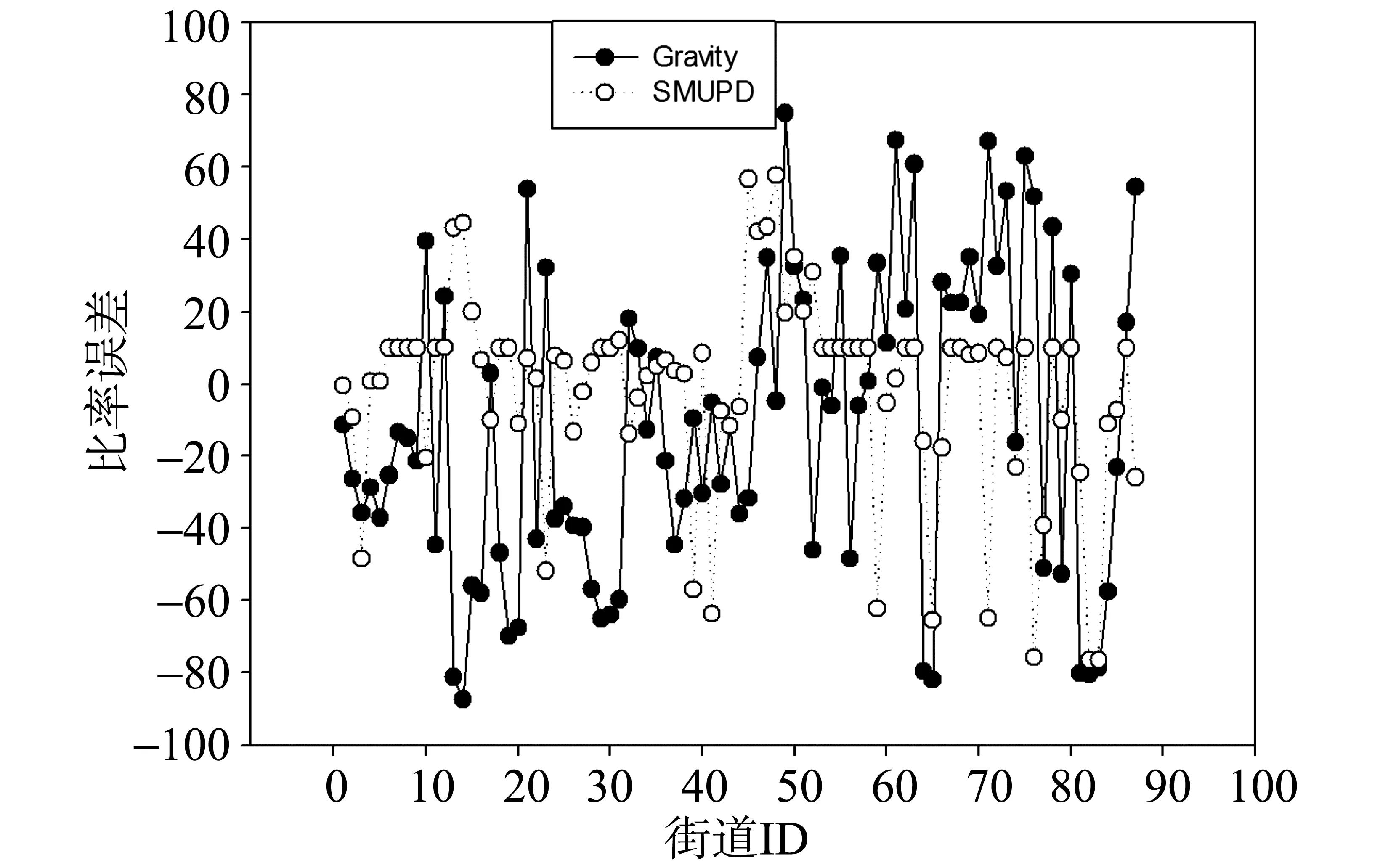
图5 重力模型(Gravity)与SMUPD模拟比率误差分布

从图(5)、表(3)可知，SMUPD模拟的大部分街道比率误差小于重力模型模拟的比率误差，且SMUPD模拟的总精度达到77.4%，明显高于重力模型模拟精度(62.4%)。

2.4.2 模拟结果居住分异分析 区位商(Location Quotient)常应用于不同群体人口分异研究中，本文采用区位商[23]对人口分布的分异状况进行分析，其公式为：

/

(17)

式中：fi为元胞i中f类型Agent的数量，ti是元胞i中总Agent数量，F和T分别是研究区域f类型Agent的数量和总Agent的数量。如果f在某个元胞的比重等于其在整个区域中的比例，则LQ=1；如果比重大于在整个区域中的比例，则LQ>1；反之，LQ<1。LQ>b表示某种居民在该居住元胞高度聚集，LQ

从图6(a1,a2)可知，广州市高收入家庭主要分布于：① 珠江两岸区域(包含荔湾区、越秀区、海珠西北部及天河区西南部)。该区域交通发达、公共服务设施便捷、拥有丰富的优质教育资源且靠近环境优雅的珠江水域，成为高收入家庭居住的首选。从上世纪末至本文研究数据时间(2006年)，此区域已建成一系列江景豪宅，如花城湾畔、椰诚苑、金海湾、中信君庭、蓝色康园以及二沙岛豪华别墅群等。② 白云山风景区周围区域。该区域由于紧靠白云山风景区且分布较多湖泊，“依山傍水”的优雅自然环境受到高收入家庭的喜爱，白云堡豪苑等一系列山景别墅分布于此。③ 天河中央商务区。作为全国三大商务区之一，此区域分布诸多的跨国金融、证券公司且交通便利，受到高收入家庭的青睐，也成为高收入家庭聚集区。

图6 按收入家庭密度分布及区位商

从图6(a2,b2)可知，相对于高收入家庭集中分布于几个区域而言，中等收入家庭即使对高收入家庭居住的高档住宅有一定的渴求，但由于家庭收入有限，大部分中等收入家庭无法支付高额的房价。因此中等收入家庭广泛分布于地段稍次于高收入家庭居住的区域，如海珠区西北部距珠江水域稍远地段，荔湾区中北部及越秀区中北部，白云区南部及天河区西南部。

从图6(a3,b3)可知，低收入家庭主要分布在白云区北部、天河区北部及海珠区东南部。即使在中高收入家庭聚集的区域也存在着部分低收入家庭的聚集区，这些聚集区主要是一些交通欠发达且公共服务设施不齐全的“城中村”，如中山大学附近的下渡村、康乐村，研究时段内珠江新城所包含的猎德、冼村及谭村等。

3 结 论

针对“自上而下”的城市人口数据空间分布化方法存在的不足，本文构建了基于多智能体的城市人口分布模拟模型(SMUPD)。智能体在居住压力作用下，根据自身经济状况及偏好对居住影响因素进行评价并选择适合的居住元胞进行搬迁，通过智能体在居住元胞不断迁居形成城市的人口分布格局，实现了以“自下而上”的方式对城市人口分布进行模拟。

根据研究区的家庭数量及类型生成对等数量的智能体，动态模拟了研究区域城市人口分布，且对人口分布所体现的分异特性进行了研究。实验结果表明：基于多智能体的城市人口分布模拟模型既取得了较好的模拟精度，又解决了原有方法在人口居住分异分析方面存在的不足，且模拟结果体现出的分异格局与研究区存在的居住分异现象大致相符，为解决人口数据空间分布化问题提供了新的途径。

城市人口分布影响因素较多，后续研究中，模型将进一步考虑经济、产业等因素对城市人口分布的影响。

参考文献：

[1]廖一兰，王劲峰，孟斌，等.人口统计数据空间化的一种方法[J].地理学报，2007，62(10)：1110-1119.

[2]卓莉，陈晋，史培军，等.基于夜间灯光数据的中国人口密度模拟[J].地理学报，2005,60(2):266-276.

[3]刘纪远，岳天祥，王英安，等.中国人口密度数字模拟[J].地理学报，2003，58(1)：17-24.

[4]YUE T X,Wang Y A,Chen S P.Numerical simulation of population distribution in China[J].Population and Environment,2003,25(2): 141-163.

[5]金君，李成名，印洁，等.人口数据空间分布化模型研究[J].测绘学报，2003，32(3): 278-282.

[6]吕安民，李成名，林宗坚，等.人口密度的空间连续分布模型[J].测绘学报，2003，32(4): 344-348.

[7]徐建刚，梅安新，韩雪培.城市居住人口密度估算模型的研究[J].遥感学报，1994，9(3)：234-239.

[8]冯健，周一星.转型期北京社会空间分异重构[J].地理学报，2008，63(8)：829-844.

[9]李志刚,吴缚龙.转型期上海社会空间分异研究[J].地理学报，2006，61(2)：199-211.

[10]陶海燕，黎夏，陈晓翔.基于多智能体的居住空间格局演变的真实场景模拟[J].地理学报，2009，64(6)：665-676.

[11]刘小平，黎夏，叶嘉安,等.基于多智能体系统的空间决策行为及土地利用格局演变的模拟[J].中国科学:D辑(地球科学) ,2006,36(11) : 1027-1036.

[12]张鸿辉，曾永年，谭荣.基于多智能体的农地非农化时空模拟与规划模型[J].测绘学报，2011，40(3)：366-372.

[13]BENENSION I,OMER I,HATNA E.Entity-based modeling of urban residential dynamics: the case of Yaffo,Tel Aviv[J].Environment and Planning B: Planning and Design,2002,29:491-512.

[14]刘小平，黎夏，陈逸敏，等.基于多智能体的居住区位空间选择模型[J].地理学报，2010，65(6)：:695-707.

[15]吴静，王铮.2000年来中国人口地理演变的Agent模拟分析[J].地理学报，20008，63(2)：185-194.

[16]肖洪，田怀玉，朱佩娟，等.基于多智能体的城市人口分布动态模拟与预测[J].地理科学进展，2010，29(3)：347-354.

[17]张文忠，刘旺，孟斌.北京市区居住环境的区位优势度分析[J].地理学报，2005，60(1)：115-121.

[18]McFADDEN D.Conditional logit analysis of qualitative choice behavior//Frontiers in Econometrics[M].ZAREMKA P,ed.New York: Academic Press，1974.

[19]徐建华.现代地理学中的数学方法[M].北京：高等教育出版社，2002.

[20]王松涛，郑思齐，冯杰.公共服务设施可达性及其对新建住房价格的影响—以北京中心城为例[J].地理科学进展，2007，26(6):78-85.

[21]BALK D L,DEICHMANN U,YETMAN G.Determining global population distribution: Methods,applications and data[J].Advances in Parasitology,2006,62: 120-154.

[22]唐华秀，马劲松，战金艳，等.江苏省人口数据离散化研究及其精度分析[J].长江流域资源与环境，2008，17(4)：506-510.

[23]俞路，赵永全.人口分布、隔离指数及其地理视角[J].市场与人口分析，2007，13(3)：1-8.