一类四次哈密尔顿系统的极限环数*

范兴宇,黄文韬,陈爱永

(桂林电子科技大学数学与计算科学学院，广西 桂林 541004)

确定Abel积分的零点个数问题和确定系统在很多项式扰动下的极限环个数密切相关，称之为弱化的Hilbert第十六问题，近些年来，对在扰动项下的哈密尔顿(Hamilton)系统

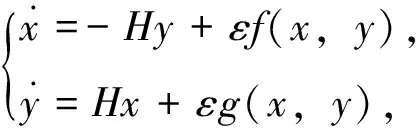
(1)

的极限环数的研究越来越受到重视[1-4]，其中H(x,y),f(x,y),g(x,y)为实系统数多项式，degH(x,y)=n+1,deg(f(x,y),g(x,y))≤n。对于扰动哈密尔顿(Hamilton)系统的极限环个数研究，可分为两类：一类是取定较小的n值，给出Abel积分的零点个数。另一类是固定H，而f,g为任意的n次扰动。关于系统(1)的一些特殊情形的极限环研究成果颇多，见文[5-8]，值得一提的是在文[9]中，作者应用分支理论与判定函数得到了Z(3,5)≥14，文[10]的作者利用定性分析的方法也得到Z(3,2m+2n)≥m+n的结论。文[11]文通过计算系统的Abel积分和数值法得到Z(3,3)≥4，本文利用文[11]的方法研究下述四次多项式扰动下地四次哈密尔顿(Hamilton)系统的极限环个数

(2)

其中x,y,α,β,γ,δ,ρ∈C,λ∈(0,1)，得到了Z(4,4)≥14。

1 预备知识

哈密尔顿(Hamilton)向量场的扰动系统

δp(x,y,δ,μ),

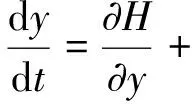
(3)

这里变量(x,y)∈R2，小参数δ∈R,0<δ≪1,μ∈Rk,二元函数H(x,y)∈Cr,r≥2。当δ=0时，则系统(3)就为哈密尔顿(Hamilton)系统。设该系统的解轨线中有闭轨线族，其表达式为：Γh={(x,y)|H(x,y)=h,h1≤h≤h2}。假定Γh关于h单调排列。对于系统(3)，定义

(4)

显然，当时，沿有，从而，系统(4)可写为

I(h)=∮Γhq(x,y,0,μ)dx-p(x,y,0,μ)dy,h∈

(5)

其中H(x,y),p(x,y),q(x,y)为x,y的实系统多项式，degH(x,y)=m+1并且max{degp(x,y),q(x,y)}≤n，记为使实代数曲线H(x,y)=h有一个紧分支Γh的所有h的值得集合，定义函数(5)为系统(3)的一个Abel积分。确定Abel积分I(h)的孤立零点个数，而此零点与极限环是相互对应的，从而研究系统的极限环个数可转化为求其Abel积分I(h)的孤立零点个数。

2 高次项扰动下的四次哈密尔顿系统的极限环

在扰动的哈密尔顿(Hamilton)系统(2)中，

(6)

其中λ∈(0,1)。针对该系统，下面我们考虑时的情形即

,.05x2-0.95x

(7)

通过计算机软件易得该系统的周期解图像，见图1。

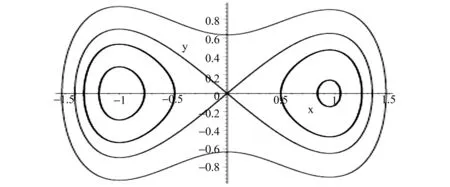
图1 四次哈密尔顿系统的周期解

由系统(2)易知

f(x,y)=0,

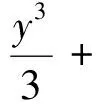
(8)

从而，该系统的阿尔贝积分为

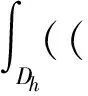
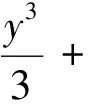
I(h)=αI00(h)+βI10(h)+

γI20(h)+δI02(h)+ρI30(h)

(9)

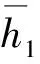
定理1 对于系统(2)|λ=0.95，若参数α,β,γ,δ,ρ选择合适的数值，则当ε→0时，系统的Abel积分(9)有14个零点，即系统至少存在14个极限环。

证明证明过程分两个部分。首先，确定合适的参数(α,β,γ,δ,ρ)的值。先应用文[11]的方法，我们考虑如下线性系统

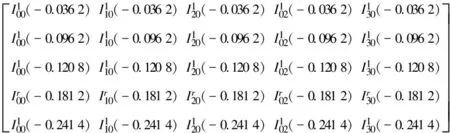
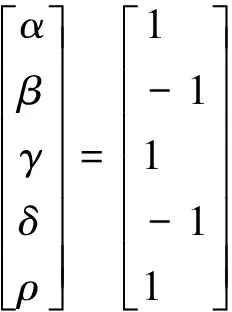
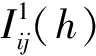
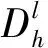
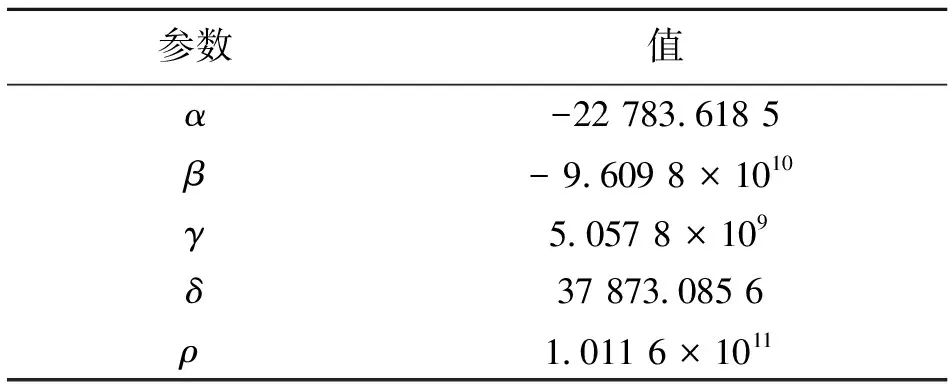
表1 参数值

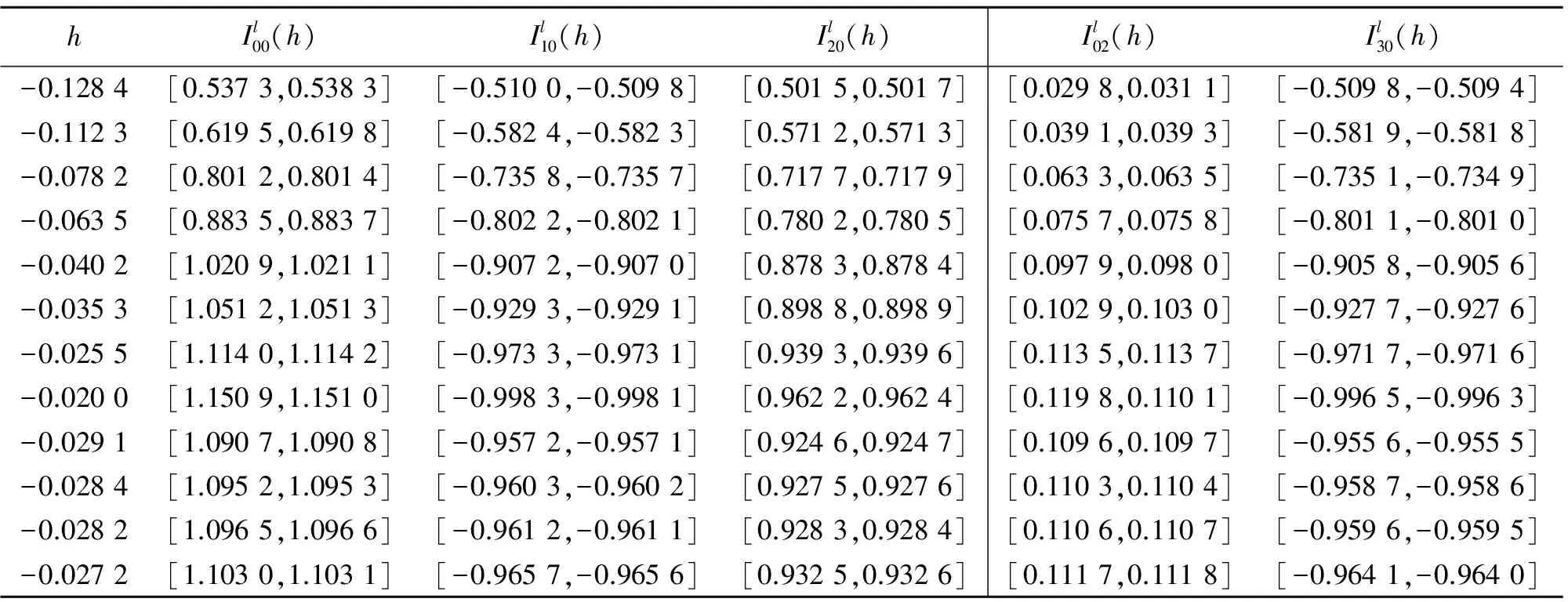
表2 左区域上的积分值

再由(9)可得Il(-0.128 4)，Il(-0.112 3)，Il(-0.078 2)，Il(-0.063 5)，Il(-0.040 2)，Il(-0.035 3)，Il(-0.025 5)，Il(-0.020 0)，Il(-0.029 1)，Il(-0.028 4)，Il(-0.028 2)，Il(-0.027 2)的值，见表3。将该表的数值反映到函数图象中，见图2。易见，在左积分区域上是连续的，且至少存在6个零点。

图2 I(h)在左区域上的图像

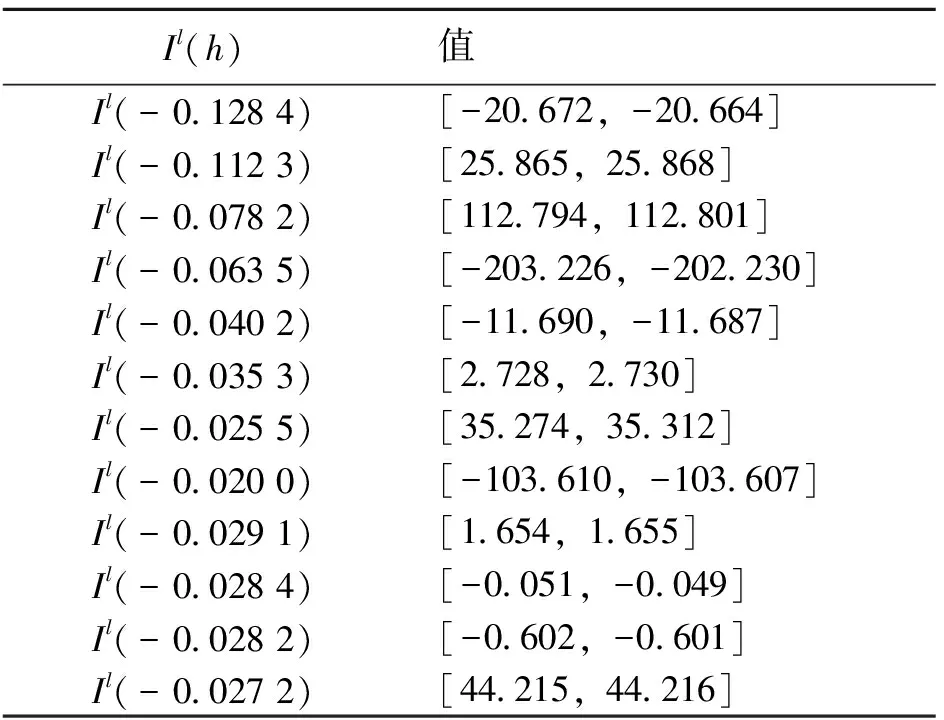
表3 Il(h)的值

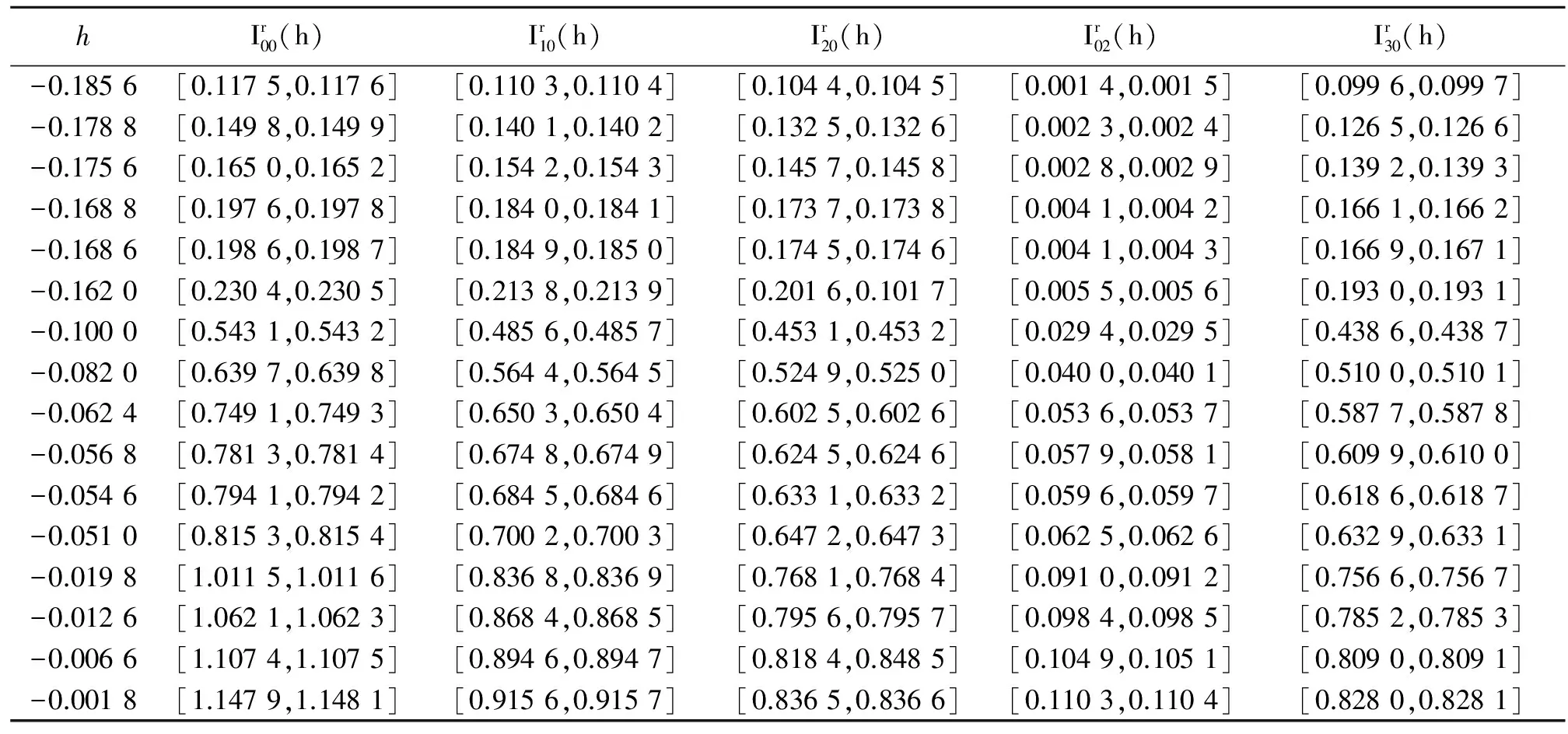
表4 右区域上的积分值

表5 Ir(h)的值

图3 I(h)在右区域上的图像

参考文献：

[1]CHEN F,LI C,LIBRE J,et al.A unified proof on the weak Hilbert 16th problem forn=2[J].J Diff Equa,2006,221(2): 309-342.

[2]CHRISTOPHER C,LI C.Limit cycles of differential equations,advanced courses in mathematics[M].CRM Barcelona Birkhäuser Verlag,Basel,2007.

[3]ECALLE J.Introduction aux functions analysables et preuve constructive de la conjecture de Dulac[M].Hermann,Pairs,1992.

[4]ROUSSARIE R.Bifurcation of planar vector fields and Hilbert’s sixteenth problem,progress in mathematics[M].Birkhäuser Verlag,Basel,1998.

[5]DUMORTIER F,LI C.Perturbations from an elliptic Hamilton of degree of four:(I)saddle loop and two saddle cycle[J].J Diff Equa,2001,176(1): 14-157.

[6]DUMORTIER F,LI C.Perturbations from an elliptic Hamilton of degree of four:(II)cuspidal loop[J].J Diff Equa,2001,175(2): 209-243.

[7]DUMORTIER F,LI C.Perturbations from an elliptic Hamilton of degree of four:(III)global center[J].J Diff Equa,2003,188(2): 473-511.

[8]DUMORTIER F,LI C.Perturbations from an elliptic Hamilton of degree of four:(IV)figure eight-loop[J].J Diff Equa,2003,188(2): 512-554.

[9]ZHOU H X,XU W,LI S,et al.On the number of limit cycles of a cubic polynomials Hamiltonian system under quintic perturbation[J].Applied Mathematic and Computation，2007,190(1): 490-499.

[10]WU C Q,XIA Y H.The number of limit cycle of cubic Hamiltonian system with perturbation[J].Nonlinear Analysis: Real World Application,2006,7: 943-949.

[11]JOHNSON T,TUCKER W.On a computer-aided approach to the computation of Abelian integrals[J].BIT Numerical Mathematics,2011,51:653-667.