一点超前数值差分公式的提出、研究与实践*

张雨浓，陈宇曦，陈锦浩，殷勇华

(中山大学信息科学与技术学院，广东 广州 510006)

数值微分是数值计算应用中的一个重要概念，是求解常微分方程和偏微分方程的重要工具[1～4]。它根据给定的离散采样点数据，使用多项式插值法、有限差分法、正则化方法或待定系数法等方法逼近目标函数在目标点处的一阶导数值[5-6]。对于有着广泛应用背景和实用性的有限差分类型的方法，人们对其研究兴趣与日俱增[5,7～10]。一般来说，若给定未知目标函数在指定区间上的离散采样点数据，可使用多点中心差分公式求远离边界的目标点的一阶导数值，以及使用多点前向差分公式和多点后向差分公式求区间边界处目标点的一阶导数值。然而，多点中心差分公式的使用需要保证目标点两端有相同数量的计算数据点，但对于靠近边界的目标点来说，它靠近边界的一边会出现数据点不足的情况，因此可能无法使用多点中心差分公式。另外，未知目标函数的一阶导数在这类目标点处可能会发生加速变化，而前(后)向差分公式只使用目标点远离边界一端的计算数据点，因此可能无法适应该变化，使得用该公式得到的一阶导数近似值误差较大。考虑到这类目标点的特殊性，需研究出一种综合三种传统有限差分公式特性的新差分公式对其进行一阶导数的近似计算。本文将针对靠近右边界目标点一阶导数的计算，将后向差分公式在形式上“前移”一点，即可得到适应该类目标点的一点超前数值差分公式。该公式参考了前(后)向差分公式在数据点利用上的不平衡性，解决了目标点单边数据点不足的问题，同时它又利用所“前移”的一点，适当调节了目标点的一阶导数估算，适应了函数在该处可能发生的一阶导数加速变化。

1 一点超前数值差分公式

基于多项式插值理论，利用采样数据点以及相应的函数值，可以通过构造插值多项式P(x)来近似求得一个未知目标函数f(x)的逼近表达式，即f(x)≈P(x)；进而，对P(x)求一阶导数便可近似得到未知目标函数f(x)的一阶数值微分公式，即f′(x)≈P′(x)[11-12]。另外，在实际应用中，数字离散系统往往是等间距地采集数据[13]，也即xi+1-xi=h(i=0,1,2,…,n)，其中h>0为采样间隔常数，为此，本文将主要研究和探讨等间距一点超前数值差分公式。

定义1[5,11,14]设未知目标函数f(x)在离散采样数据点xi处的函数值为f(xi)，i=0,1,2,…,n。若存在n次多项式Pn(x)=a0+a1x+ … +anxn满足条件Pn(xi)=f(xi)，则称Pn(x)为未知目标函数f(x)的n次插值多项式。

引理1[5,11,14]如果x0,x1,x2,…,xn是采样区间[a,b]上(n+1)个互不相同的数据点，且未知目标函数f(x)的(n+1)阶导数连续(记f∈C(n+1)[a,b])，则对任一x∈[a,b]，存在c∈(a,b)使得f(x)=Pn(x)+Rn+1(x)，其中Pn(x)为未知目标函数f(x)的插值多项式，Rn+1(x)为余项且Rn+1(x):=f(n+1)(c)(x-x0)(x-x1)…(x-xn)/(n+1)!。

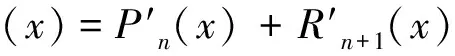
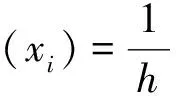
(1)

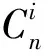
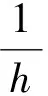
(2)

对于公式(2)，分别令n=1,2,…,15，经过计算，即可推导出二至十六个数据点的等间距一点超前数值差分公式。其中，表1列出了二至八个数据点的等间距一点超前数值差分公式，而九至十六个数据点的等间距一点超前数值差分公式在附录中列出。

表1 二至八个数据点的等间距一点超前数值差分公式

观察表1可以发现，二数据点等间距一点超前数值差分公式即为传统的二数据点前向差分公式，而三数据点等间距一点超前数值差分公式即为传统的二数据点中心差分公式。

2 计算机验证与实践

由于一点超前数值差分公式在数据点的利用上具有了“前瞻性”，有效调节目标点的导数值计算，因此能很好地解决因目标函数的一阶导数加速变化而影响微分计算精度的问题。为验证一点超前数值差分公式的这种特性，这里选取两个目标函数f1(x)=sin(x)和f2(x)=arctan(x)来进行计算机数值实验，用一点超前数值差分公式和后向差分公式分别计算这两个目标函数在一阶导数变化最快的地方的一阶导数近似值，再通过比较两个公式的求导效果研究一点超前数值差分公式的性能优势。

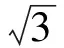
如前所述，二数据点等间距一点超前数值差分公式即为二数据点的前向差分公式，而三数据点等间距一点超前数值差分公式即为二数据点的中心差分公式，而前人已对它们进行了有效性研究[5,11]，因此本文不再对它们展开更深入的探讨。这里将使用四至八个数据点的等间距一点超前数值差分公式进行实验。

一般来说，数值微分计算的结果只有计算机表示能力的一半精度[11]，因此，我们在实验中使用优化步长。另外，考虑到在实际工程应用中所得到的样本数据精度有限，现对实验中所使用的目标函数样本数据作出精度限制，统一精确到小数点后9位，并以四数据点等间距一点超前数值差分公式为例求其优化步长。

用ei(i=0,1,2,3)表示表1中四数据点等间距一点超前数值差分公式中对应样本函数f(xi)(i=0,1,2,3)的舍入误差，再根据式(1)中微分公式的余项，可得到f′(xi)的误差项表达式[11]：

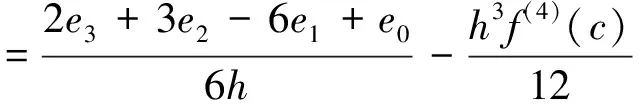
设每个误差ei的量级为ε，同时误差是积累的，且|f(4)(x)|≤M，则可得到如下误差界：

通过求函数g(h)=2ε/h+Mh3/12的最小值可得到优化步长，从而使误差界最小。设g′(h)=0，可得-2ε/h2+Mh2/4 = 0，即h4= 8ε/M，这样可得到优化步长：

(3)

对于目标函数f1(x)=sin(x)，使用边界|f1(4)(x)|≤|sin(x)|≤1=M和值ε=0.5×10-9，代入式(3)计算可得优化步长h=0.007 952 707，可以看到h=0.01时最接近优化值。用同样的方法可得到关于这两个目标函数其它多点等间距一点超前数值差分公式的优化步长。为了方便比较，这里同时算出后向差分公式在同样情况下的优化步长，并根据两个差分公式的优化步长差异，统一选择用于计算机实验的优化步长，如表2所示。

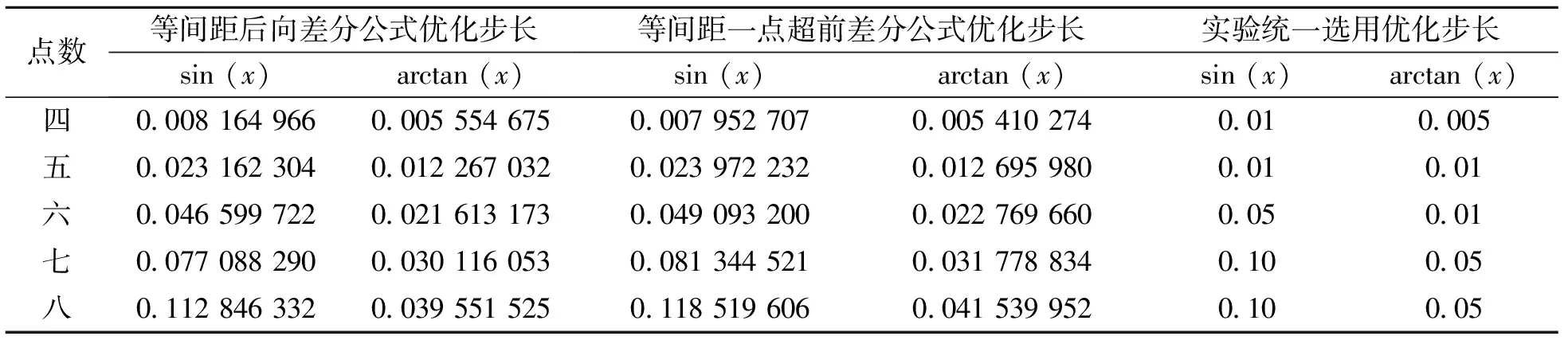
表2 四至八个数据点的等间距数值差分公式的优化步长

综合以上分析，我们将使用表2中实验统一选用的优化步长，分别利用后向差分公式和一点超前数值差分公式，求目标函数f1(x)=sin(x)和f2(x)=arctan(x)分别在x1=1.571和x2=0.577处一阶导数近似值，并以近似值与真值之差的绝对值作为实验计算误差进行比较分析，如表3所示。

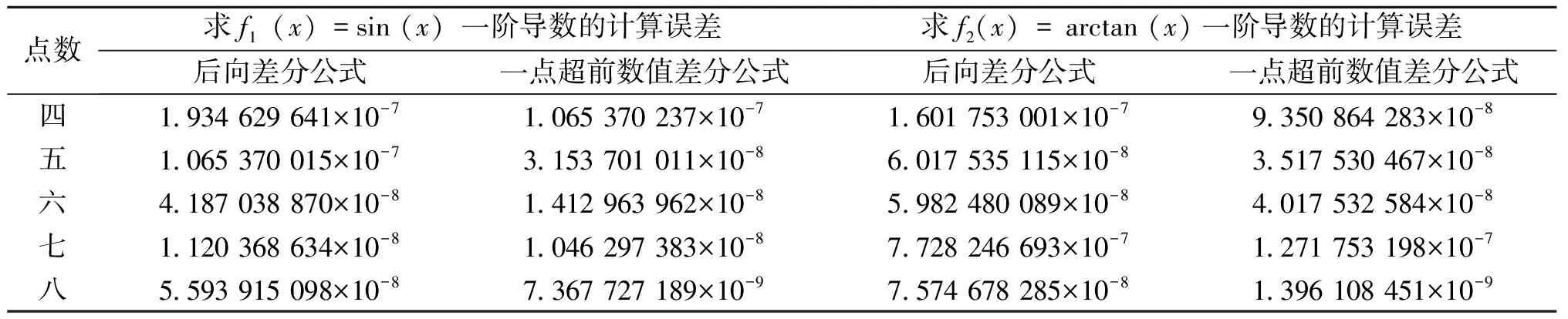
表3 目标函数f1(x)=sin(x)和f2(x)=arctan(x)一阶导数的求解误差

分析表3可以发现，使用一点超前数值差分公式计算目标函数导数时计算误差均小于使用后向差分公式计算目标函数导数时计算误差。这说明了，一点超前数值差分公式的求导性能优于后向差分公式，而且，当目标函数的一阶导数在目标点处加速变化时，一点超前数值差分公式能很好地适应该变化，使计算得到的一阶导数值具有更高的精度。

3 结 论

一阶数值微分在科学研究中有着重要的应用。而作为常用的数值微分方法，有限差分法包含了传统的前向差分公式、后向差分公式以及中间差分公式，它们在计算目标函数在指定区间边界和中部目标点的一阶导数时体现出高度的方便性和有效性。然而对于靠近区间边界的部分目标点，因其两端的计算数据点个数具有明显的不平衡性，点数较多的多点中心差分公式可能无法使用。而且目标函数的一阶导数在目标点处可能加速变化，对于只考虑单边数据点的前(后)向差分公式来说，它们可能无法调节由该变化带来的误差影响。而一点超前数值差分公式正是针对上述方法的缺点而研究出来的新的有限差分公式，它具有对数据点利用的不平衡性和对目标函数一阶导数加速变化的适应性，使实际的求导性能优于后向差分公式，因此成为一种更为方便和高效的差分算法。计算机数值实验进一步验证表明：一点超前数值差分公式可以取得较好的一阶导数估计精度。

附录九至十六个数据点的等间距一点超前数值差分公式。

前文已列出了二至八个数据点的等间距一点超前数值差分公式，考虑到方便其他研究者和应用者对公式的深入研究和使用，此处我们再列出九至十六个数据点的等间距一点超前数值差分公式，如表4所示。

表4 九至十六个数据点的等间距一点超前数值差分公式

参考文献：

[1]ZHANG Y N,JIANG D C,WANG J.A recurrent neural network for solving sylvester equation with time-varying coefficients [J].IEEE Transactions on Neural Networks,2002,13(5): 1053-1063.

[2]ZHANG Y N,GE S S.Design and analysis of a general recurrent neural network model for time-varying matrix inversion [J].IEEE Transactions on Neural Networks,2005,16(6): 1477-1490.

[3]ZHANG Y N,CHEN K.Comparison on Zhang neural network and gradient neural network for time-varying linear matrix equation AXB = C Solving[C]∥ Proceedings of International Conference on Industrial Technology Chengdu,China,2008.

[4]MA W M,ZHANG Y N,WANG J.MATLAB simulink modeling and simulation of Zhang neural networks for online Time-varying Sylvester Equation Solving[C]∥ Proceedings of International Joint Conference on Neural Networks.Hong Kong,China,2008: 286-290.

[5]张雨浓，郭东生，徐思洪，等.未知目标函数之一阶数值微分公式验证与实践[J].甘肃科学学报,2009,21(1): 13-18.

[6]LI J P.General explicit difference formulas for numerical differentiation[J].Journal of Computational and Applied Mathematics,2005,183: 29-52.

[7]郭莹莹，余向阳.光学Bloch方程的数值解法[J].中山大学学报:自然科学版,2005,44(5): 108-110.

[8]孙建平,赵亚红.二阶差分系统正解的存在性[J].甘肃科学学报,2001,14(3): 7-10.

[9]KHAN I R,OHBA R,HOZUMI N.Mathematical proof of closed form expressions for finite difference approximations based on taylor series[J].Journal of Computational and Applied Mathematics,2003,150: 303-309.

[10]田瑞,李明,滑斌.有限差分法求解方同轴线的特性[J ].甘肃科学学报,2007,19(1): 1112113.

[11]JOHN H M，KURTIS D F.数值方法(MATLAB版)[M].周璐，陈渝，钱方，等译.4版.北京：电子工业出版社，2009.

[12]ZHANG Y N,MA W M,YI C F.The Link between Newton Iteration for Matrix Inversion and Zhang Neural Network(ZNN)[C].Proceedings of IEEE Conference on Industrial Technology,2008:1-6.

[13]FRANKLIN G F,POWELL J D,NAEINI A E.自动控制原理与设计[M].李中华,张雨浓，译.5版.北京: 人民邮电出版社,2007.

[14]李建良，蒋勇，汪光先.计算机数值方法[M].南京：东南大学出版社，2000.