参考节点嵌入最短距离估算在图聚类中的应用
温菊屏,林冬梅
(1.佛山科学技术学院 电子与信息工程学院,广东 佛山528000;2.佛山科学技术学院 信息与教育技术中心,广东 佛山528000)
0 引 言
图聚类算法是一种分析社会关系网络的有效算法,它可以发掘社会关系网络中的子团体,对社会关系网络的分析有重大意义,包括提高互联网信息服务,发掘网络舆论导向等作用。图聚类有很多不同的方式,比较具代表性的有:Markov聚类[1]、谱聚类、基于密度的聚类[2]和基于划分的聚类[3]等。
本文主要研究基于划分的聚类算法,此算法使用距离来衡量点与点之间的相异度。由于社会关系网络图中的节点没有坐标值,所以只能采用具有坐标值无关特性的距离算法进行聚类,比如最短路径算法和随机漫步算法[4]等。其中,最短路径算法问题是图论研究中的一个经典算法问题,是本文研究的主要内容。
最短路径算法旨在寻找图(由结点和路径组成)中两结点之间的最短路径。其中,Dijkstra算法以及A*[5]搜索都是很有代表性的最短路径算法,由于要遍历计算的节点很多,所以效率低。最短路径算法在交通网络中应用很广泛,比如google map、GPS,用户给定两个地点a、b,要求计算出这两点之间的最短路径,由于是在线查询,没有预存储阶段,所以在线查询时间很长。为了快速响应用户的请求,需要有更为高效的算法计算两点之间的距离。
文献 [6]中提到了参考节点嵌入算法思想,该算法是从所有点中选择比较少量的参考点,预先将参考点与其他点之间的距离计算存储下来,在需要计算两点距离时,通过预先存储的距离,计算出两点之间近似估算距离。本文对最短路径算法做了改进,引入基于参考节点嵌入的最短距离估算方法来近似获得两点之间的距离。从理论和实验来比较两种距离算法时间复杂度的大小,并且用估算的近似距离和真实距离相比,计算距离相对误差率,实验证明利用改进后的距离算法计算的近似距离,相对于真实距离误差很小,但极大缩短了计算时间。
1 最短路径算法距离的计算
文中最短路径算法采用最有代表性的Dijkstra算法,它用于计算一个节点到其他所有节点的最短路径。
Dijkstra算法的缺点是时间复杂度大,分析如下:假设一个连通的大图一共有n个顶点,一共有m条边,则针对最短路径算法而言,一个点到所有n个点的时间复杂度为O(n*logn+m),则n个点到所有n个点的时间复杂度为O(n*n*logn+n*m)。最坏情况下 m=O(n2),因此时间复杂度的最坏情况为O(n3)。
2 基于参考节点嵌入的最短距离估算
2.1 算法思想
一个图通常表示为G=(V,E,w)。其中V是顶点的集合,E是边的集合,w:E→R是一个边权重函数,把一条边映射成一个实数域上的权重。如果一个图是无权图,那么每条边的权就是1。
(1)从V中选择d个参考点:v1、v2、……vd,计算这d个参考点到V中每个点之间的最短路径距离,将其预先存储下来。
(2)求任意两点之间的最短路径距离,假设第一个点为s,第二个点为t,dist(s,t)表示s到t的最短路径距离,dist(s,t)的计算方法如下:由于参考点vi和s、t构成一个三角形,根据三角形两边之和大于第三边的原理,dist(s,t)<dist(s,vi)+dist(vi,t)(i=1、2、3……d),则可以取 min(dist(s,vi)+dist(vi,t))作为最接近s、t两者之间的真实最短路径的距离,其中dist(s,vi)、dist(vi,t)通过查询预先存储的距离获得。
2.2 参考点的选择
从V中选择d个参考点,其中选择的方法有很多种,比如随机选择法、基于度的大小选择法。本文考虑到社会关系网络中,由于比较重要的人联系人多,故选择他们作为参考点比随机选择更为合理,则算法中根据每个节点的度大小进行降序排列,选择度数最大的前d个节点作为参考节点。
2.3 时间复杂度分析
基于参考节点嵌入的最短距离估算,距离矩阵的计算分两个部分进行:第一个部分是计算度数最大的d个点到其他所有点的距离,其时间复杂度为O(d*n*logn+d*m);第二个部分是通过d个参考点来计算剩下n-d个点的近似距离,对于两个点之间距离dist(s,t)的计算,需要查2d个距离,时间复杂度为O(d),由于图是无向图,那么剩下n-d个点,以每个点为起点,计算它与所有其它点之间距离的时间复杂度为O((n-d)*(n-d)*d),故两个部分时间相加,则时间复杂度为:O(d*n*logn+d*m+(n-d)*(n-d)*d),由于d<<n,则时间复杂度最大值为n2。由此可见,相对于最短路径距离算法时间复杂度而言,时间复杂度大大降低。
3 最短距离估算在图聚类中的应用
由于基于划分的聚类算法具有简单、快速并有效处理大规模数据等诸多优点,它已经成为经典并应用最广泛的聚类方式之一,主要包括k-means算法和k-medoids算法,本文采用的是k-medoids的聚类算法。
基于划分的聚类算法是使用距离来衡量点与点之间的相异度。由于社会关系网络图中点没有坐标值,所以选择与坐标值无关的最短路径距离作为点与点之间相异度的衡量是行之有效的方法,但是,计算所有点对之间的最短路径算法,例如Dijkstra和Floyd-Warshall算法具有时间复杂度大的缺点,因此需要找一种复杂度低的算法来计算所有点对之间的最短距离,在保证精确度的同时,降低时间复杂度。
参考节点嵌入(reference node embedding)算法思想被广泛应用在各种网络数据上,包括社会关系网络[6-9],公路网络[10],因特网等等,用于快速的估算两点之间的最短距离,例如在公路网络中查询两个地点之间的最短路径[10],或者在因特网中查询最近的服务器以减少客户端的访问延迟。另外对于参考节点嵌入算法思想,在计算机理论研究领域也有一些研究成果[11-12],着重于给出这种估算最短距离的一个误差上界和复杂度的分析[13-15]。参考节点嵌入的核心思想就是选择一些参考节点,用预先计算出参考节点到所有点的最短距离作为一种索引,利用这些预先算好的距离和三角不等式关系,快速处理用户的在线查询。本文的贡献在于,在图聚类的问题中,引入最短路径作为一种有效的距离衡量,并且采用了参考节点嵌入的思想来快速计算所有点对之间的最短路径,在保证精度的同时,降低时间复杂度,提高运行效率。
4 实 验
4.1 实验数据
实验数据来源于一个真实的图——DBLP数据集(http://www.informatik.uni-trier.de/~ley/db/)。在实验中选用来自数据库、数据挖掘、信息检索和人工智能这4个研究领域的参考文献数据,从中挑选出这4个领域内最高产的前1000名作者,构建他们的合著者关系大图。在该图中,每一个节点表示一个作者,每一条边表示两个作者之间的合著关系。在选择的1000个点中,有68个是相对孤立的点,对于不连通的点,得到的最短路径是无穷大,为了保证做最短路径的查询都得到有意义的解,选择其中一个最大的连通子图,该子图包含932个节点。
4.2 实验步骤
(1)使用Dijkstra算法和基于参考节点嵌入的最短距离估算算法,分别计算出精确距离矩阵和近似距离矩阵,同时测试计算距离矩阵所需的时间,比较这两种算法运行时间的长短。
(2)根据精确距离矩阵和近似距离矩阵计算距离相对误差率。
(3)在使用k-medoids算法时,分别使用精确距离矩阵和近似距离矩阵进行聚类,根据衡量指标density数值大小,来判断两种距离算法是否达到相同的分类效果。
(4)在使用k-medoids算法时,采用基于参考节点嵌入的最短距离估算算法,将最大的连通子图分成若干类,根据程序运行得到的每个子类里作者名单,判断实验分类与实际情况是否吻合,验证是否达到良好的分类效果。
4.3 测试时间
为了验证两种算法运行时间的长短,对程序采集数据,Dijkstra算法所需要的时间为16.022s。基于参考节点嵌入的最短距离估算算法所需要的时间,随着参考节点数目d值的增加,程序运行的时间也随之增加,具体数据值和变化趋势如表1和图1所示。
4.4 距离相对误差率
由于基于参考节点嵌入的最短距离估算算法,是基于有限个参考点得到的近似距离,与Dijkstra算法得到的精确距离有一定的偏差,其中误差随着d值的增大逐渐降低,直到误差率为0,当d=400时,距离相对误差率降到0.004433,误差率极小,具体数据值和变化趋势如表2和图2所示。
4.5 衡量指标
为了在节省运行时间的情况下,达到与Dijkstra算法同样的分类效果,d的取值不能太小,也不能太大,d值太小则误差率太大,d值太大则运行时间增加,通过试验得到当d=400时,采用基于参考节点嵌入的最短距离估算算法的运行时间大约是Dijkstra算法时间的一半,分类效果相当。为了表现分类效果,在这里将给出一个衡量指标density。假设图为无向图,首先统计整个大图,在没有分割之前,一共有n条边,接着分别计算k类中每类包含的点之间的边数,假设分别为n1、n2、……nk,最后计算density=(n1+n2+……+nk)/n。最理想的状态是:在切分大图时,都是在没有边的地方切割,则density的结果为1。density的值越大说明分割的方法越好。将算法用程序实现之后,运行程序采集数据:在每一个k值的情况下,都要进行10次分类(为了保证可比性,两个算法用到的随机聚类中心点采用相同的点),取10次分类比率的平均值作为当前k值下的最终比率denstiy,根据两个算法density值的大小,可以比较出分类效果的好坏。假设density1是使用Dijkstra算法得到的比率,density2是基于参考节点嵌入的最短距离估算算法得到的比率。实验数据证明,当d=400时,density2和density1大致相同,说明取得了相同的分类效果。density1、density2两者数据如表3所示,变化趋势如图3所示。

表1 基于参考节点嵌入的最短距离估算算法的运行时间

图1 基于参考节点嵌入的最短距离估算算法的运行时间

表2 距离相对误差率

图2 距离相对误差率

表3 两种距离算法density数值
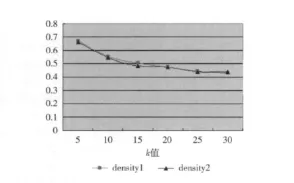
图3 两种距离算法density数值
从表3和图3我们可以看出:①对于两种距离算法来说,k值增大,density值下降,这个趋势都是相同的,因为分的类越多,类与类之间的边就越多,而类内部的边就少,所以density下降;②使用Dijkstra算法与基于参考节点嵌入的最短距离估算算法,获得的density大致相同,达到同样的分类效果。
4.6 聚类效果
为了验证基于参考节点嵌入的最短距离估算图聚类算法的有效性,在使用k-medoids算法时,采用d=400时对应的近似距离矩阵进行聚类,将最大的连通子图数据分成7小类,实验结果表明每类数据均为相同领域合著关系比较紧密的作者列表,实验分类情况和实际情况吻合,分类效果理想。在这7小类中,选择其中具有代表性的4类,其中每类只列举出比较多产的前20位作者姓名,如图4和图5所示。

5 结束语
针对社会关系网络图中点没有坐标值的问题,本文提出选用与坐标值无关特性的最短路径距离作为点与点之间相异度的衡量是一种行之有效的方法。同时,为了克服最短路径算法时间复杂度大的缺点,对最短路径算法进行改进,引入基于参考节点嵌入的最短距离估算思想。实验证明,基于参考节点嵌入的最短距离估算算法在取得较好的聚类效果的同时,大大降低了运行时间,提高了效率。
[1]Venu Satuluri,Srinivasan Parthasarathy.Scalable graph clustering using stochastic flows:Applications to community discovery [C].Paris,France:Proceedings of the 15th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining,2009:737-746.
[2]XU Xiaowei,Nurcan Yuruk,FENG Zhidan,et al.SCAN:A structural clustering algorithm for networks [C].San Jose,CA,USA:Proceedings of the 13th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining,2007:824-833.
[3]ZHANG Jiangpei,YANG Yue,YANG Jing,et al.Algorithm for initialization of K-Means clustering center based on optimized-division [J].Journal of System Simulation,2009,21(9):2586-2590(in Chinese).[张健沛,杨悦,杨静,等.基于最优划分的K-Means初始聚类中心选择算法 [J].系统仿真学报,2009,21(9):2586-2590.]
[4]Graph clustering based on structural/attribute similarities [C].Lyon,France:Proceedings of the VLDB Endowment,2009:718-729.
[5]Goldberg A V,Harrelson C.Computing the shortest path:A*search meets graphs theory [C].Vancouver,Canada:Proceedings of the Sixteenth Annual ACM-SIAM Symposium on Discrete Algorithms,2005:156-165.
[6]Potamias M,Bonchi F,Castillo C,et al.Fast shortest path distance estimation in large networks [C].Hong Kong:Proceed-ings of the 18th ACM Conference on Information and Knowledge Management,2009:867-876.
[7]Gubichev A,Bedathur S,Seufert S,et al.Fast and accurate estimation of shortest paths in large graphs [C].Toronto,Canada:Proceedings of the 19th ACM International Conference on Information and Knowledge Management,2010:499-508.
[8]Sarma A D,Gollapudi S,Najork M,et al.A sketch-based distance oracle for web-scale graphs [C].New York,NY,USA:Proceedings of the Third ACM International Conference on Web Search and Data Mining,2010:401-410.
[9]Rattigan M J,Maier M,Jensen D.Using structure indices for efficient approximation of network properties [C].Philadelphia,PA,USA:Proceedings of the 12th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining,2006:357-366.
[10]Kriegel H P,Kr?oger P,Renz M,et al.Hierarchical graph embedding for efficient query processing in very large traffic networks [C].Hong Kong:Proceedings of the 20th International Conference on Scientific and Statistical Database Management,2008:150-167.
[11]Kleinberg J,Slivkins A,Wexler T.Triangulation and embedding using small sets of beacons [C].Rome,ITALY:Proceedings 45th Annual IEEE Symposium on Foundations of Computer Science,2004:444-453.
[12]Thorup M,Zwick U.Approximate distance oracles [J].Journal of the ACM,2005,52(1):1-24.
[13]HU H,LEE D L,LEE V S.Distance indexing on road networks [C].Seoul,Korea:Proceedings of the 32nd International Conference on Very Large Data Bases,2006:894-905.
[14]Samet H,Sankaranarayanan J,Alborzi H.Scalable network distance browsing in spatial databasdes [C].Vancouver,Canada:Proceedings of the 2008ACM SIGMOD International Conference on Management of Data,2008:43-54.
[15] WEI F.TEDI:Efficient shortest path query answering on graphs [C].Indianapolis,IN,USA:Proceedings of the International Conference on Management of Data,2010:99-110.

