ATC与CO方法对比及其在卫星设计问题中的应用

吴蓓蓓，黄 海，吴文瑞

（北京航空航天大学 宇航学院，北京100191）

0 引 言

解析目标分流（ATC）方法是密歇西根大学的Michelena等于1999年基于产品开发过程的提出的一种复杂系统设计方法［1］，主要用于汽车、飞机等设计领域［2－3］；协同优化（CO）方法是斯坦福大学的Kroo等人于1994年针对航空系统学科间组织困难和通讯困难提出的一种两级多学科设计优化（MDO）方法［4］，在航天飞机、卫星和星座系统中得到广泛应用［5－6］。两种方法既存在相似性也有不同之处，本文在两种方法基本原理研究的基础上重点对两种方法的计算效率进行对比，已有研究中，密歇西根大学的Allison等人通过数学解析算例说明了两种方法的不同点和互补性［7］，文献 ［8］将两种方法应用到飞机设计中，得到了相近的结果，但上述研究对两种方法的计算效率无对比研究。同时，由于ATC方法在航天器MDO问题中的应用研究较少，本文将进一步将ATC方法的应用某卫星设计问题，推进其在航天器设计领域的应用。

1 基本原理

本节介绍两种方法的基本原理并讨论二者的相似和区别，它们是ATC与CO方法对比研究的基础。

1.1 ATC方法

ATC方法起初面向的是可分解为层级问题的产品设计，如图1所示，设计指标自系统到子系统到部件不断分流，同时各级响应由下而上不断反馈，系统、子系统和部件级各单元问题分别独立求解，上下级间交叠优化直到满足收敛条件优化过程停止。以第i级第j个问题Pij为例，其优化表达式如式（1）所示

式中：Xij＝［xij，yij，y（i＋1），R（i＋1），εR，εy］T——设 计 变 量，它包含局部设计变量xij，共享设计变量yij，子问题共享变量y（i＋1）和子问题响应矢量 R（i＋1），约束容差εR和εy。其中，y（i＋1）＝｛y（i＋1）k｝k，R（i＋1）＝｛R（i＋1）k｝k，y（i＋1）k，R（i＋1）k——问题Pij第k个子问题的共享变量和响应矢量，k＝1，2，…cij，cij——子问题数目；，——问题 Pij的Rij和yij参 数 在 父 代 复 制；，——问 题 Pij的和参数在子代的复制；gij，hij——不等式约束和等式约束。

原始ATC方法将容差εR和εy也作为设计变量，增加了优化问题的维数，Michalek和Papalambros使用罚函数法［9－10］，将一致性约束直接放入优化目标降低了优化问题维数。2005年，Tosserams等人用广义拉格朗日罚函数代替二次罚函数，并引入交替方向乘子法协调各级优化问题，进一步提高了ATC方法的计算效率［11］，2010年Tosserams等人又发展了ATC方法的非层级表达式，使之适用于一般的复杂系统设计问题［12］。

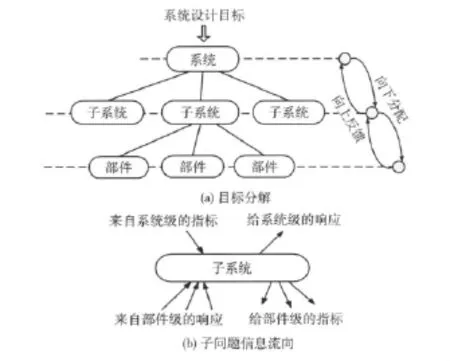
图1 ATC方法

1.2 CO方法

CO方法将复杂系统设计问题沿学科边界进行分解，各学科在满足本学科约束的情况下独立独立进行优化，系统级通过一致性约束协调学科级问题之间的差异。按照标准CO方法，系统级优化问题可以描述为

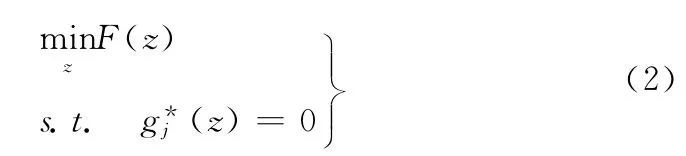
式中：F（z）——系统级目标函数，z——系统级设计变量，由学科间共享设计变量和耦合参数变量组成；——系统级约束，又称为一致性约束，通过调用学科优化得到，j∈1，2…n，n为学科数目。学科（子系统）级优化问题可以描述为

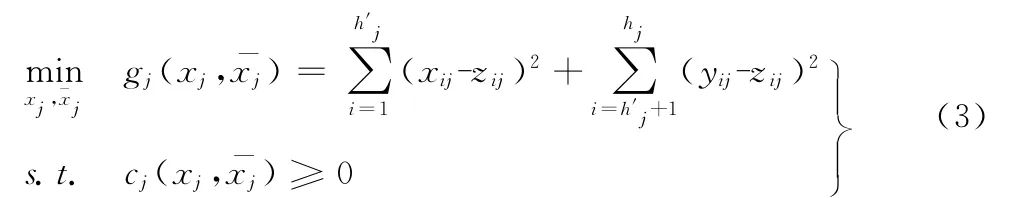
式中：xj＝｛xij｝i——j学科共享设计变量，i＝1，2，…h′j；——j学科局部设计变量；yij——j学科输出到其他学科的耦合参数，i＝＋1，＋2，…hj；zij——系统级分配到j学科的指标参数矢量，i＝1，2，…hj；cj——j学科约束。

CO方法由于系统一致性约束而存在一系列缺陷，比如系统级约束函数不光滑，系统级约束函数在最优解处的雅可比矩阵奇异，学科级优化问题拉格朗日乘子为0等问题。面对CO方法的缺陷，相关学者提出了一系列改进措施来改善上述问题，如约束松弛法、响应面法、罚函数法等［13］。

1.3 原理对比

表1列出了ATC与CO方法在起源、级数、分解标准、表达式、优化过程、信息通讯、收敛性等方面的对比信息，可以看出ATC与CO方法虽然在问题的表达式方面相似，但是在起源、适用级数、分解标准，特别是优化过程、通讯方式、收敛性等方面二者却不同。在ATC方法中，上下级之间采用交替优化的策略，子系统优化后向系统级返回共享变量和响应参数，而CO方法中，学科优化嵌套于系统优化中，在系统级优化每一步均要调用一次完整的学科级优化，学科优化后向系统返回一致性约束（即学科优化目标）。

2 解析算例测试对比

该节使用ATC和CO方法分别求解两解析算例，分别给出测试问题在两种方法下的优化表达式、协调策略优化结果对比，重点对两种方法的计算效率进行对比研究。算例一分解后子问题之间仅存在共享设计变量，算例二子问题之间除了包含共享变量外，还存在耦合参数［13］，两者求解过程略有不同。

2.1 算例一

算例一如式（4）所示，该优化问题精确最优解为X＝［0.8，1.6］和f＝3.2000，为了进行算法测试可以将其看为如图2所示的两个子问题组成

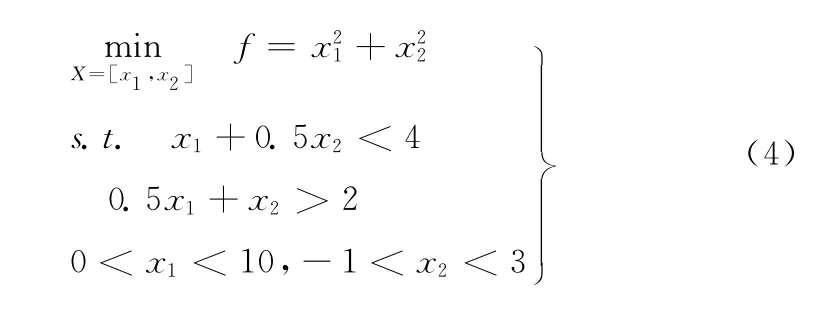
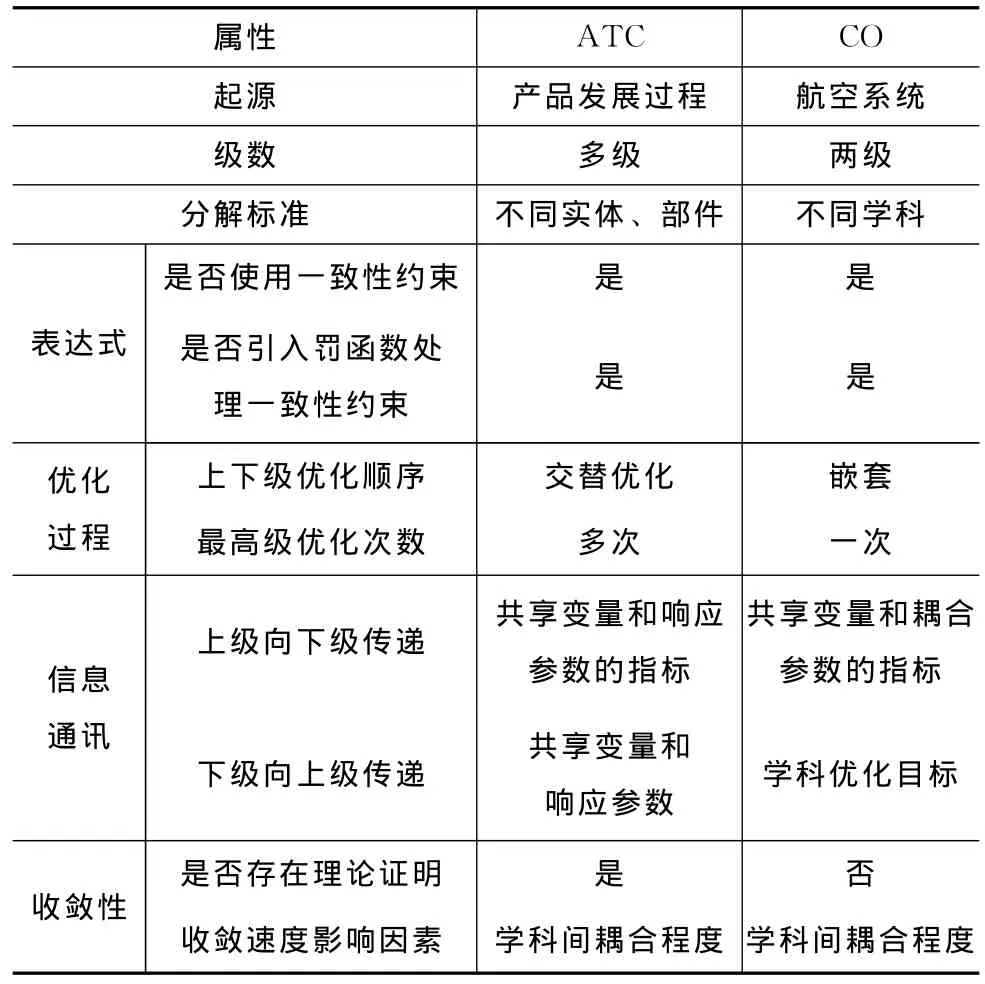
表1 ATC和CO方法特性对比

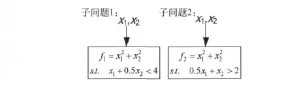
图2 算例一分解

2.1.1 问题表达式

（1）ATC方法

按照ATC方法，系统级优化表达如式（5）所示，为了避免罚因子过大带来的病态问题，采用广义拉格朗日罚函数处理偏差项［11］

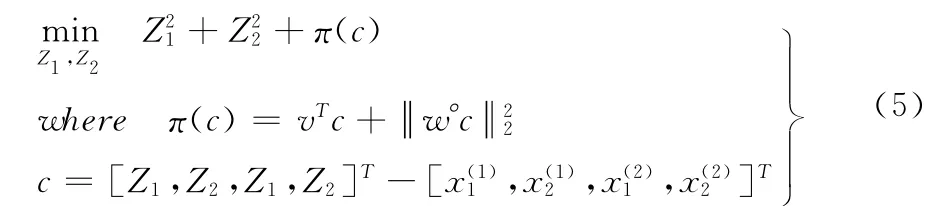
式中：Z1，Z2——系统级设计变量；π（c）——广义拉格朗日罚函数，c——系统指标和子系统响应差，上标（1）和（2）分别代表子系统1和2的响应，v为拉格朗日乘子矢量，w为罚因子矢量。以子问题1为例的优化表达式为

式中：π（c1）——子系统1的优化目标，同样采用拉格朗日函数形式，v1，w1——对应的拉格朗日乘子矢量和罚权重矢量。

（2）CO方法

按照CO方法，系统级优化问题表达如式（5）所示，为了改善一致性约束带来的缺陷，采用罚函数法处理一致性约束

式中：J1，J2——学科1和2的优化目标，以子问题1为例的优化表达式

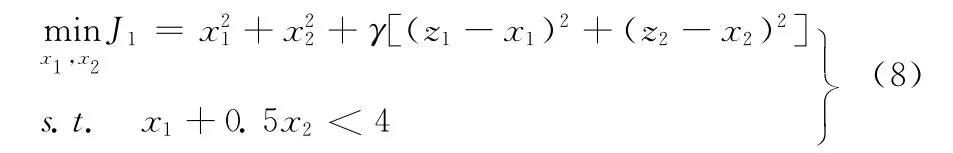
式中：x1，x2——学科1设计变量；γ——罚参数；J1由系统目标和一致性约束组成。

2.1.2 协调策略

ATC方法的协调过程如图3所示，拉格朗日乘子，罚权重初值和增长步长分别为0，1和2。CO框架如图4所示，系统优化内嵌学科优化，罚参数取为1。

2.1.3 优化结果

寻优算法采用序列二次规划（NLPQL）算法，系统和子系统（学科）问题均采用解析法计算敏度，收敛精度为1e－5，一致性约束要求不超过1e－4，选定5组初值分别进行计算，所需运算次数和结果误差的平均值见表2。

从表2可以看出，ATC和CO计算精度相当；就系统级函数运算次数来说，ATC方法约是CO方法的3倍；就子系统函数运算次数来说（以子系统1为例），CO方法约是ATC方法的3倍；就系函数总运算次数说，CO方法约是ATC方法的1.6倍，表明采用ATC方法的计算效率高于CO方法。

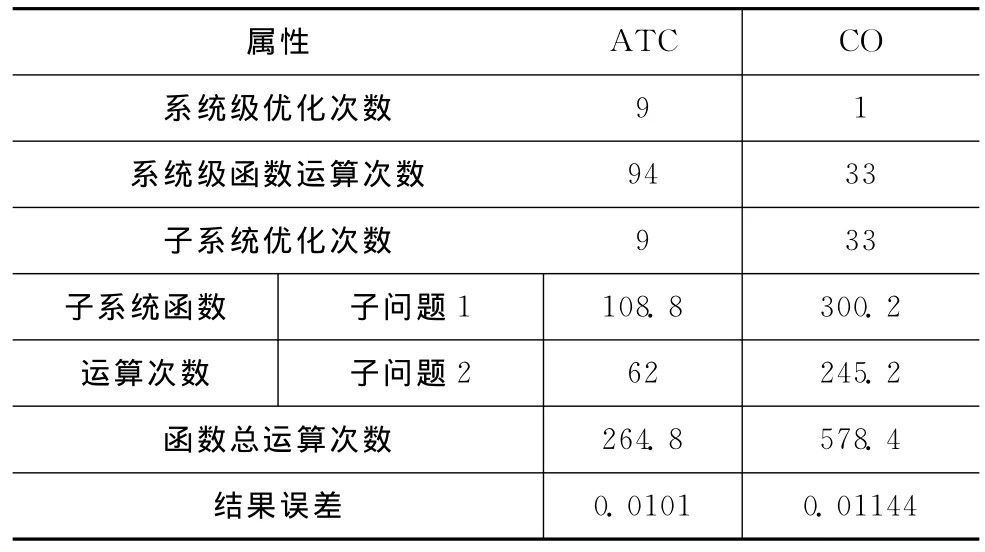
表2 算例一优化结果对比

2.2 算例二

算例二如式（9）所示，该问题全局最优解为X＝［3.03，0，0］和f＝8.00286，将其看作如图5所示的两子问题组成，y1和y2为学科间耦合参数

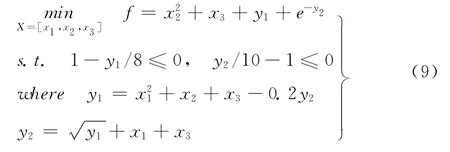
图5 算例二分解

算例二问题表达式、协调过程同算例一基本类似，。对于耦合参数，通过将其作为设计变量实现子问题之间的解耦。对于优化过程，ATC方法求设置拉格朗日乘子，罚权重初值和增长步长分别为0，0.1和1.2；对于CO方法，通过求解序列罚参数下的系统级优化问题来获得满足一致性约束的优化结果，罚参数序列初值为1，增长因子为1.2。对于寻优算法，同样采用NLPQL法，但敏度计算通过有限差分法计算，并计入函数运算次数，同样选取5组初值进行计算，所需运算次数和结果误差的平均值如表3所示。

从两种方法运算次数和结果精度的对比可以得出与算例一相似的结论。该例中CO方法结果精度略高，但CO方法函数总运算次数约是ATC方法的2倍，所以就计算效率而言，ATC方法相对CO方法有较大优势。

2.3 结 论

由以上两个算例可以看出ATC方法通过减少子系统优化和函数运算次数，使整个优化过程的计算效率高于CO方法。对于大型分布分析式问题，可以按子系统边界进行分解，采用ATC方法组织设计过程，减少子系统分析设计次数，提高设计效率。

表3 算例二优化结果对比

3 卫星设计问题应用

卫星设计涉及有效载荷、轨道、电源、结构、控制、推进多个学科，是典型的复杂系统设计问题，本文将ATC方法应用到文献 ［14］描述的对地观测卫星总体参数MDO问题中，检验该方法在航天器设计问题中的有效性。

3.1 问题描述

该问题以地面分辨率G和覆盖带宽φ的综合指标最大化为优化目标，考虑有效载荷、姿控、电源、结构和推进等5个子系统的设计变量和约束条件（具体见文献 ［14］）。将原问题按照子系统边界进行分解，形成一个系统级和五个子系统级优化问题，按照ATC方法形成问题表达式，系统级问题可以描述为

式中；P（X）——系统优化目标；X——系统级设计变量，h，hsa，Lsa，Lt——共享设计变量，其它为耦合参数变量，各符号含义如表4所示。π（c）——广义拉格朗日罚函数，c——系统指标和子系统响应之间的偏差矢量，t1，t2，…，t5——系统分配到有效载荷、姿控、电源、结构和推进子系统的指标矢量，r1，r2，…，r5——子系统对应响应参数矢量。

以姿控子系统为例的子系统级优化问题表达式为

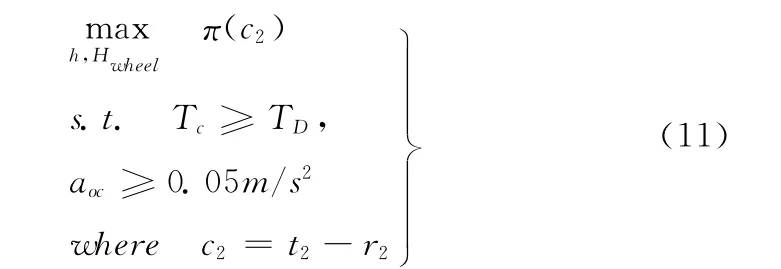
式中：Hwheel——动量轮容量，为姿控子系统局部设计变量；Tc——飞轮控制力矩；TD——外界环境干扰力矩；aoc——轨控加速度；c2——姿控子系统指标响应偏差，t2和r2如式（12）所示

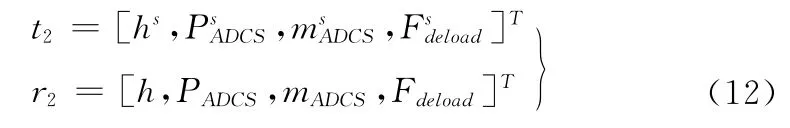
表4 符号含义

3.2 结 果

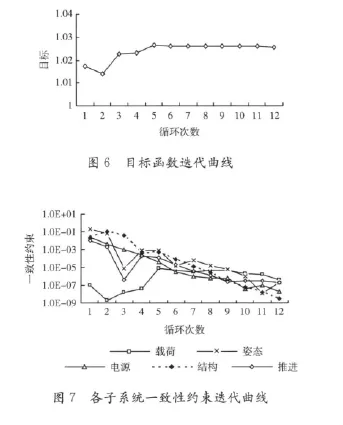
拉格朗日乘子和罚权初值以及罚权步长分别选取0和1以及1.3，各子系统一致性约束要求不超过10－6。经过12次循环，优化过程停止，表5给出了采用ATC方法目标函数优化结果，与文献 ［14］结果一致。图6和图7分别给出了目标函数和子系统一致性约束的迭代曲线，随着系统和子系统之间的协调，目标函数得到优化，同时一致性约束也逐渐满足，表明ATC方法求解卫星MDO问题是有效的。

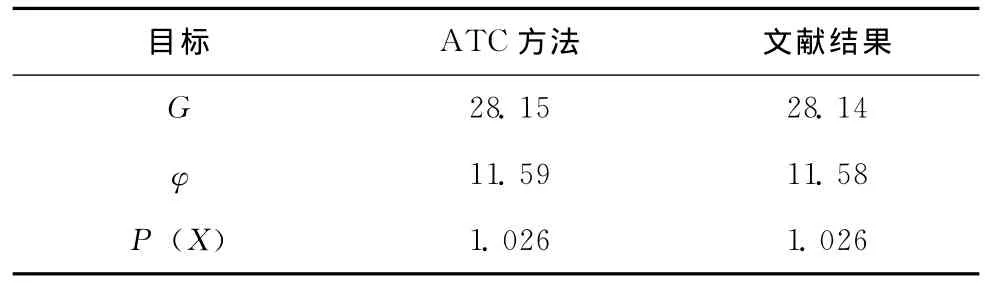
表5 优化结果对比

4 结束语

ATC和CO作为两种基于分解思想的复杂系统设计方法，在计算表达式以及系统指标、一致性约束等关键术语方面存在相似性，但在上下级（系统和子系统）之间优化策略、通讯方式和适用级数等方面存在不同。本文针对实际问题求解中两种方法的计算效率问题，采用两个解析算例进行测试求解，结果表明ATC方法相对CO方法可以大大减少子系统优化分析次数，进而提供整个优化过程的计算效率。最后通过ATC方法在卫星设计问题中的求解得到正确的结果，表明ATC方法在航天器设计问题中应用的有效性。

［1］Michelena N，Kim H M，Papalambros P Y.A system partitioning and optimization approach to target cascading ［C］.Munich，Germany：12th International Conference on Engineering Design，1999：1－6.

［2］Kokkolaras M，Louca L，Delagrammatikas G，et al.Simulation－based optimal design of heavy trucks by model－based decomposition：An extensive analytical target cascading case study［J］.International Journal of Heavy Vehicle System，2004，11（3）：403－433.

［3］Allison J，Walsh D，Kokkolaras M，et al.Analytical target cascading in aircraft design ［R］.Reston，Va：American Institute of Aeronautics and Astronautics，2006.

［4］Kroo I，Altus S，Braun R，et al.Multidisciplinary optimization methods for aircraft preliminary design ［R］.Development and Application of the Collaborative Optimization Architecture in a Multidisciplinary Design Environment，1994.

［5］Yokoyama N，Suzuki S，Tsuchiya T.Multidisciplinary design optimization of space plane considering rigid body characteristics［J］Journal of Spacecraft and Rockets，2007，44（1）：121－131.

［6］WU Beibei，HUANG Hai，WU Wenrui.Multidisciplinary optimization of main parameters of spacecraft with sub－vehicles［J］.Acta Aeronautica et Astronautic Sinica，2011，32（4）：628－635.［吴蓓蓓，黄海，吴文瑞.带子星航天器总体参数多学科设计优化 ［J］.航空学报，2011，32（4）：628－635.］

［7］Allison J，Kokkolaras M，Zawislak M，et al.On the use of analytical target cascading and collaborative optimization for com－plex system ［C］.Rio de Janeiro，Brazil：6th World Congress on Structural and Multidisciplinary Optimizations，2005：1－10.

［8］Allison J，Roth B，Kokkolaras M，et al.Aircraft family design using decomposition－based methods ［R］.Reston，Va：American Institute of Aeronautics and Astronautics，2006.

［9］Michalek J J，Papalambros P Y.An efficient weighting update method to achieve acceptable consistency deviation in analytical target cascading ［J］.Transactions of the ASME，2005，127（5）：206－214.

［10］ Michalek J J，Papalambros P Y.Technical briefs weights norms and notation in analytical target cascading ［J］.Journal of Mechanical Design，2005，127（5）：499－501.

［11］Tosserams S，Etman L F P，Papalambros P Y，et al.An augmented lagrangian relaxation for analytical target cascading using the Alternation directions method of multipliers ［J］.Structural and Multidisciplinary Optimization，2006，31（3）：176－189.

［12］Tosserams S，Kokkolaras M，Etman L F P，et al.A nonhierarchical formulation of analytical target cascading ［J］.Journal of Mechanical Design.2010，132（5）：1－13.

［13］Roth B D.Aircraft family design using enhanced collaborative optimization［D］.CA，U.S.：Stanford University，2008：21－23.

［14］TAN Chunlin，PANG Baojun，ZhANG Lingyan，et al.Multidisciplinary optimization in earth observation satellite main parameters［J］.Journal of Beijing University of Aeronautics and Astronautics，2008，34（5）：529－532（in Chinese）. ［谭春林，庞宝君，张凌燕，等.对地观测卫星总体参数多学科优化 ［J］.北京航空航天大学学报，2008，34（5）：529－532.］