基于Delaunay三角网矿体和采空区储量计算算法与实现＊

李 华，宁化展，丁希旺

（滨州市水利勘测设计研究院测量队，山东 滨州256612）

0 引 言

数字地形模型（DTM）是以离散分布的平面点来模拟连续分布的地形，是野外地表勘测成果的数字化展现，广泛的应用于地理信息系统各领域中。Delaunay三角网是DTM的主要实现形式，用一系列互不交叉、重叠的连接在一起的三角形网来表示地形［1］。

矿产储量，简称储量，一般是指经过地质勘探、基建勘探和生产勘探后，经勘查证实存在矿体，探明其空间分布、产状、形态、规模和质量，可以开发利用的原地矿产资源量［2］。根据各种探矿工程和技术手段所得到的资料及信息（一般是钻孔资料），通过一定的计算方法计算矿产的地下埋藏量，这一系列的工作称之为矿产储量（资源量）计算。

矿产资源储量的计算方法有断面法、算术平均法、等值线法等，这些算法都是在矿产资源勘探时期估算矿产资源储量的计算方法，这些算法并不适于计算矿体采空区的开采量。为此，提出了一种基于矿体区域的采空区矿体储量计算方法，根据矿体采空区范围及回采率计算出矿体资源已开采量和矿体资源剩余储量。

1 矿体区域Delaunay三角网的生成

基本Delaunay三角网生成有以下四个步骤：凸壳的生成过程、初始三角网生成过程、离散点插入初始三角网过程、局部优化过程。矿产资源的储量计算是在已知矿产资源分布边界，以及区域钻孔资料数据计算所得，根据钻孔的稀疏程度还要对离散钻孔点进行插值运算。因此论述的Delaunay三角网生成有以下六个步骤：

1）点差值过程：由于钻孔点不多以及区域边界太长，为了使生成的三角网最优及矿产量的计算更准确需要对边界点及钻孔点进行插值运算。

2）凸壳生成过程：凸壳［3］是包含所有离散点的最小多边形，一般的凸壳构造方法只是找出了最少点的多边形，对于多点在一条凸壳边上的情况只是找出了两个端点而中间点却没有找出来，这种情况对矿体的建模有影响，为此采用一种夹角与距离最小［4］的凸壳构造方法。

3）初始三角网生成过程：利用凸壳点生成初始三角网（如图1所示）。

4）点插入过程：将点集中的离散点（不包含凸壳点）依次插入［5］，在初始三角形链表中找出三角形外接圆包含插入点的三角形（称为该点的影响三角形），剔除查找出的影响三角形的公共边，将此插入点同查找到的影响三角形的全部顶点连接起来，完成一个点在Delaunay三角形链表中的插入，如图2所示。

5）局部优化过程：局部优化算法是为了生成Delaunay三角网。算法的基本含义：对由两个公共边组成的四边形进行判断，如果其中一个三角形的外接圆包含第四个顶点，则这个四边形的对角线互换，如图3所示。

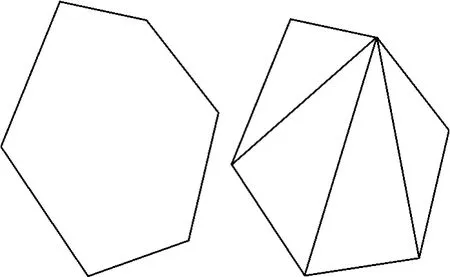
图1 初始三角网

图2 点插入

图3 局部有化过程

6）三角形剔除过程：根据已知边界条件，将不符合条件的三角形剔除，如图4所示。若只是按照三角形三个点都在边界上这个条件来剔除可能会剔除一些合法的三角形，因此还要加上内切圆圆心是否在边界内这个条件。算法描述如下：①判断三角形的三个顶点是否位于边界上，②若果不是都在边界上删除三角形，如果均位于边界上，求出内切圆的圆心，判断是否位于边界内，若是三角形保留否则三角形剔除［4］，如图4所示。

图4 三角形剔除

2 采空区域Delaunay三角网的生成

矿山储量动态管理中，遇到的主要问题是两个三维实体：采空区与矿体［6］。需要管理的内容是二者相交部分的矿产量，此矿产量的计算首先要求采空区的平面区域与矿体Delaunay三角网区域的相交Delaunay三角网区域，如图5所示，再求出此Delaunay三角网区域的矿产量。

图5 采空区域

根据采空区平面二维边界求其与矿体表面Delaunay三角网相交部分的Delaunay三角网的算法思想如下：

1）如图5所示，内边界点也要参与Delaunay三角网的构建；

2）以内边界的一条边开始查找此边影响的三角形（即：与此边相交的三角形）并依次对查找的三角形编号记录下来，判断三角形在边界外侧的顶点与此三角形跟影响边的交点组成的是三角形还是四边形，若是三角形直接连接，若是四边形根据Delaunay三角形优化原则连接四边形的一条对角线构成两个三角形，如图6所示。

影响三角形的查找方法如下：以起始边的一个端点开始，首先查找以此端点为顶点的三角形并判断那个三角形与此边相交求出交点，如此得到第一个影响三角形；找出与第一个三角形影响边共边的三角形并求出此三角形与起始边的交点，如此得到第二个影响三角形，依次循环直到求出的交点为起始边的另一端点，这样就找出了所有影响三角形及它们与影响边的交点；

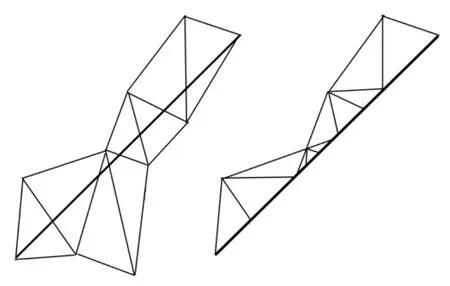
图6 边界影响三角形

3）依照步骤2）求出其它边界边的影响三角形和每个影响三角形与边界边的交点，并按步骤2）的方法生成边界外侧的三角网；

4）边界点和边界上的交点与边界内的点重新生成Delaunay三角网，如图7所示。

图7 三角网生成

3 基于Delaunay三角网的储量计算方法

根据Delaunay三角网模型，直接利用Delaunay三角形进行体积计算，体积计算如下：先求出每个Delaunay三角形所构成立柱体的体积Vi，再把区域内所有立柱体的体积相加，从而得到整个矿区内矿产体积储量V，再乘以矿产密度，就是矿体重。因此，地质体的体积计算也就是计算每个三棱柱［7］，如图8所示的体积，然后累积和就是地质体的体积。

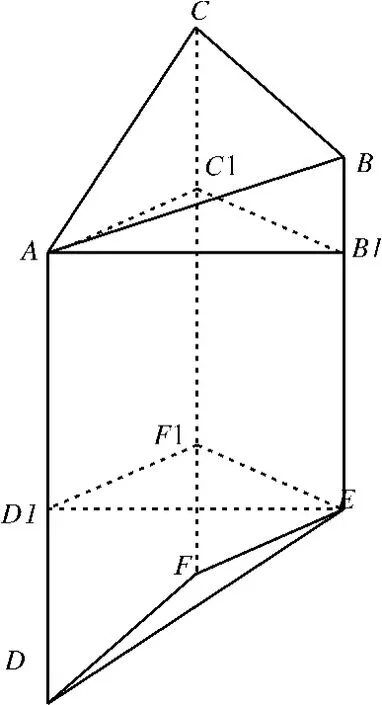
图8 矿体线性模型

已知三棱柱上表面三角形三个点A，B，C和下表面三角形三个点D，E，F的（X，Y，Z）坐标，求三棱柱的体积算法思想如下：

1）找出上表面三角形点Y值最小的点A和下表面三角形点Y值最大的点E，并以这两点为基准做横切面把三棱柱分成一个直三棱柱和两个四棱锥体。

2）根据A，B，C三点的坐标值可求出BB1、CC1、C1B1、AC1、AB1的长度，进而求出四边形CC1B1B的面积S.在三角形AB1C1中根据求出的三边长可求出A到边B1C1的高h，即四棱锥的高。上表面四棱锥的体积v＝S＊h／3.

3）A，E两点的高程差即是直三棱柱的H，根据第二步求出的三角形AB1C1三个边长可求出直三棱柱的横截面面积S，则直三棱柱的体积V＝S＊H.

4）按照步骤②的方法求出下表面四棱锥的体积，三个体积累计求和即为此三棱柱的体积，多个三棱柱体积的累计即得到地质体的体积。

图9 矿体面状模型

图9、10示出了以滕州曹庄煤矿三层煤数据及采空区数据生成的煤层模型和采空区模型。选中煤层或任一采空区都可计算出其体积、表面积及投影面积。体积及面积信息在窗体状态栏左下角显示，如图11所示。

图10所示浅色区域为选中的矿体采空区区域，其体积为2 894 621.0m3与ARCGIS计算的体积2 888 418.6m3相似率达0.997 8，实践证明此算法是正确有效的。

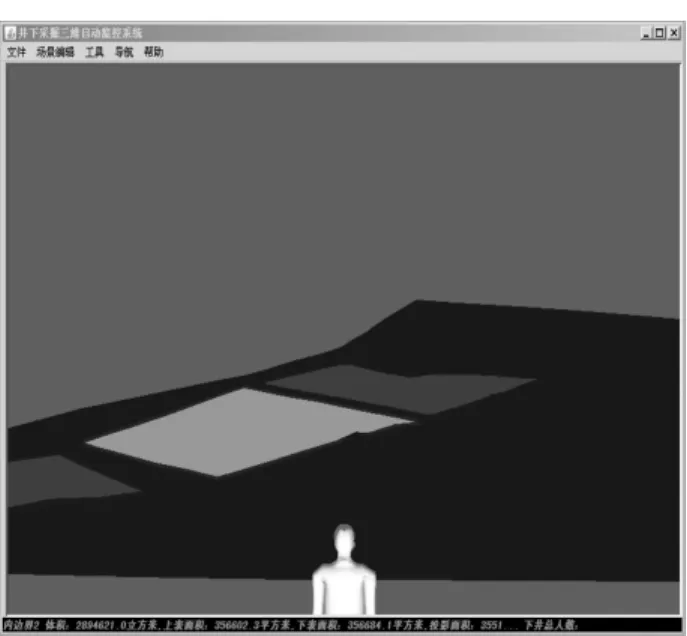
图10 矿体面状模型

图11 状态栏

4 结 论

根据钻孔的坐标及属性数据库，利用java3D可视化技术，通过对Delaunay三角形生成过程中点集进行封闭性判断，生成任意地区Delaunay三角网，结合钻孔属性数据库，对任意区域矿产储量进行计算，为计算任意区域矿产储量与可视化提供了一种新思路，该方法不仅克服算术平均法误差大及其它方法难以自动实现的缺点，而且为矿山管理提供可视化查询与分析功能。

［1］ 袁 翰，李伟波，陈婷婷.对构建Delaunay三角网中凸壳算法的研究与改进［J］.计算机工程，2007，33（7）：70－72.

［2］ 蒋 锐，宋焕斌，朱杰勇.基于三维栅格数据的露天矿山储量动态监测研究与应用［J］.矿产与地质，2009，23（5）：469－472.

［3］ 刘永和，王润怀，齐永安.一种非凸包边界约束不规则三角网生成算法［J］.测绘科学，2008，33（3）：79－81.

［4］ 宁化展，田茂义.带有边界条件的Delaunay三角网生成算法的研究与实现［J］.全球定位系统，2010，35（4）：39－42.

［5］ 徐道柱，刘海砚.大量约束边条件下Delaunay三角网的快速生成［J］.测绘工程，2007，16（3）：6－10.

［6］ 张尹军.矿产资源储量动态监测的问题及建议［J］.商品与质量，2010，（7）：74－75.

［7］ 张渭军，孔金玲，翁晓鹏.基于钻孔数据Delaunay三角网的矿产储量计算［J］.测绘科学，2010，35（4）：57－58.