三天线GPS姿态解算误差分析＊

陈 杨，唐 艳，周 伟，徐昕诰

（61081部队，北京100094）

0 引 言

GPS最初设计主要用于精密定位及授时，随着计算机技术及载波相位差分技术的发展成熟，利用多个GPS天线组成载体姿态测量系统，对载体姿态进行实时或事后测量已经成为GPS研究领域的一个方向。利用GPS进行载体姿态测量精度取决于GPS测量的精度，同时还与其他一些因素有关，如天线的夹角、基线的长短等［1－2］。给出利用三天线直接求解载体姿态参数方法，探讨了影响三天线姿态解算误差的因素，给出实例，并分析在给定条件下GPS姿态解算误差的大小。

1 三天线GPS姿态解算模型

1.1 天线架设及载体平台坐标系的建立

天线架设如图1所示，选天线1的相位中心为载体平台坐标系的原点，天线1指向天线2的连线与载体运动方向相同，此方向为载体平台坐标系的Y轴正方向，载体平台坐标系的X轴垂直于Y轴，并指向载体前进方向右侧，载体平台坐标系的Z轴与其X，Y轴垂直，构成右手坐标系。载体姿态定义在本坐标系上，横滚角为绕载体平台坐标系Y轴旋转的角度，向右旋转为正，向左为负，用r表示；俯仰角为绕载体平台坐标系X轴旋转的角度，向上旋转为正，向下为负，用p表示；航向角为绕载体平台坐标系Z轴旋转的角度，从真北方向起算，0～360°，用h表示。

图1 天线架设示意图

1.2 坐标系转换

利用GPS进行载体姿态测量，得到的原始数据是各历元GPS天线相位中心在WGS－84坐标系下的结果［3］。为了计算载体姿态，首先以天线1的定位结果作为当地水平坐标系的坐标原点将天线2和天线3的定位结果，转换成当地水平坐标系中的坐标。设天线1在某历元的定位结果为

式中：w表示WGS－84坐标系下的坐标；L，B，H分别表示经度、纬度和高度。则任一点在WGS－84坐标系下的坐标Xw可以通过Bursa－Wolf坐标系转换模型得到其在以点为原点的当地水平坐标系下的坐标值。

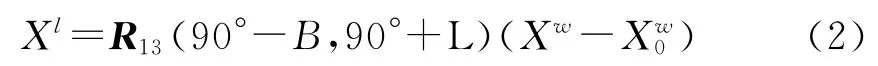
式中，Xl为当地水平坐标系下的坐标值。

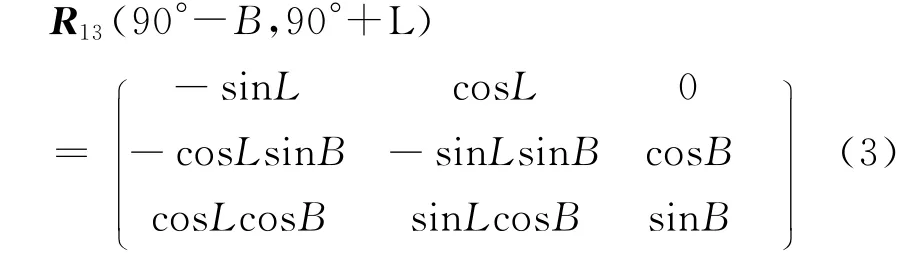
选定当地水平坐标系与载体坐标系原点相同，位于天线1的相位中心。则当地水平坐标系可以通过三次坐标旋转得到相应的载体坐标系，而转换参数正好就是三个姿态角r，p，h.

式中，Xb为载体坐标系下的坐标值。

在天线安装的时候，三个天线的相位中心在载体坐标系下的坐标值已知，故可通过式（4）解算出姿态参数。

1.3 姿态参数计算

天线在载体上的安装位置如图2所示，天线1与天线2的距离为L12，天线1与天线3的距离为L13，天线1相位中心与天线2相位中心一起构成Y轴，天线3偏离Y轴的角度为θ23，则可得各天线在载体坐标系下的坐标分别为b1＝（0，0，0）T，b2＝（0，L12，0）T，b3＝（L13sinθ23，L13cosθ23，0）T.设各天线相应的当地水平坐标系坐标分别为l1＝（0，0，0）T，l2＝（x2，y2，z2）T，l3＝（x3，y3，z3）T，则有

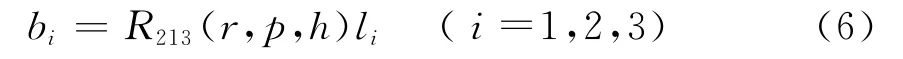
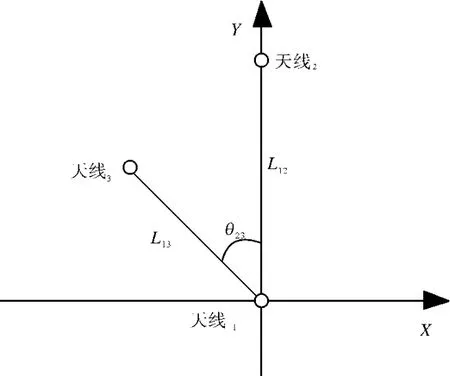
图2 天线平面示意图

将天线2的当地水平坐标代入上式可得

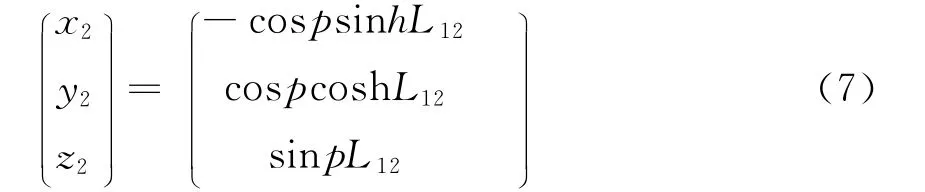
整理得到航向角和俯仰角的计算公式

得到了航向角和俯仰角之后，将天线3的当地水平坐标l3＝（x3，y3，z3）T代入式（6）可得

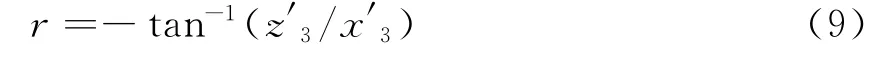
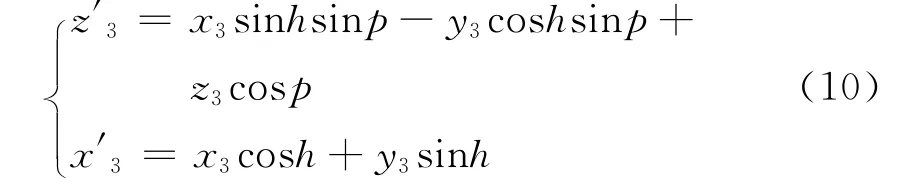
式（8）、（9）即为三天线GPS姿态参数计算公式。

2 姿态解算误差分析

2.1 航向角误差分析

对式（8）微分，利用误差传递公式，忽略各坐标分量之间的相关性，则航向角的标准误差为［4－5］

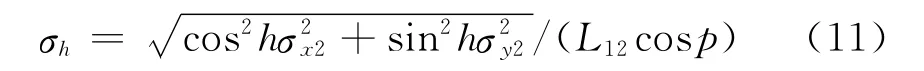
为简化分析，可认为各天线当地水平坐标系下的各坐标分量的误差是独立同分布的，因此可设

式（11）可以简化为

当前主流技术的GPS载波相位测量定位的精度指标可以达到水平2cm＋2ppm，垂直3cm＋3 ppm（RMS），不妨取σ＝3cm，取p的范围为0°～30°，L12的取值范围为2～20m，航向误差σh如图3所示

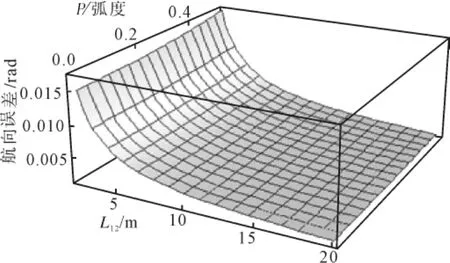
图3 航向误差示意图

从图中可见，在GPS载波相位测量误差一定的情况下，影响航向误差的主要因素是基线的长度，基线越长，航向误差越小。此外俯仰角的大小也是航向误差的一个影响因素，俯仰角绝对值越小，航向误差也越小，俯仰角为零式航向误差最小。

2.2 俯仰角及横滚角误差分析

对式（8）、（9）分别微分，利用误差传递公式，可分别得到俯仰角和横滚角的误差。

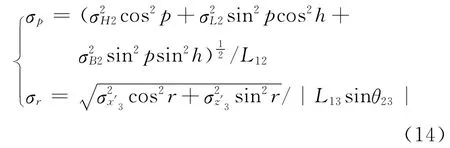
同样为简化分析，可认为各天线WGS－84坐标系下的各坐标分量的误差是独立同分布的，因此可设

则俯仰角误差可简化为

可以看出，俯仰角的误差大小与定位误差大小成正比，与基线长度成反比。

对于天线3，可认为其当地水平坐标系下的各坐标分量的误差是独立同分布的，因此可设σx3＝σy3＝σz3＝σ，对式（10）利用误差传递公式可知

因此，横滚角误差计算式可以简化为

取σ＝3cm，θ23的范围为10°～170°，L12的取值范围为2～20m，横滚角误差σr由图4示出。

从图4可以看出，横滚角误差σr与基线长度成反比，还与三天线夹角θ23有关，当三天线夹角成90°时，横滚角误差最小。

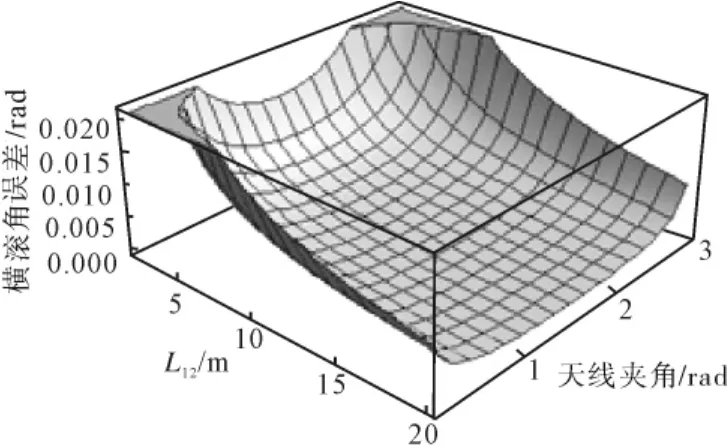
图4 横滚角误差示意图

3 结 论

利用三个GPS天线的观测数据可以对载体姿态进行测量，载体姿态测量精度主要取决与GPS载波相位测量定位的精度和基线长度，在载体长宽有限的情况下，提高GPS测量精度，合理的对布置GPS天线的相对位置，都可以提高三天线GPS的测姿精度。

［1］ 李征航，黄劲松.GPS测量与数据处理［M］.武昌：武汉大学出版社，2005：50－51.

［2］ 何海波.高精度GPS动态测量及质量控制［D］.郑州：解放军信息工程大学测绘学院，2002.

［3］ 韩慧群.GPS姿态测量系统研究与开发［D］.哈尔滨：哈尔滨工程大学，2006.

［4］ 许江宁，朱 涛，卞鸿巍.GPS姿态测量综述［J］.海军工程大学学报，2003，15（3）：17－36.

［5］ 罗建军，袁建平.航天器GPS姿态估计算法研究［J］.宇航学报，2001，21（3）：62－65.