考虑负荷管理影响的配电网孤岛划分方法

程 寅，周步祥，林 楠，王学友

（1.四川大学电气信息学院，成都 610065；2.四川电力职业技术学院，成都 610071）

智能电网是经济和技术发展的必然结果，智能电网的主要特征之一就是分布式电源的大量接入和充分利用［1，2］。孤岛是配电网引入DG以后出现一种新的运行方式，在IEEE1547－2003标准中已经不再禁止有意识的孤岛的存在，而是鼓励供电方和用户通过技术手段实现DG的孤岛运行，通过合理计划形成的孤岛可以保证重要负荷的供电，减小停电面积，提高供电可靠性，保证电能质量，这有利于电网的可靠运行和分布式发电技术的发展［3～6］。

需求侧管理技术是智能电网最重要的组成部分之一，我国正在开展电力需求侧管理，并将大量配置相应的负荷管理系统［7］。负荷管理作为需求侧管理的一项基本工作，对配电网孤岛划分有着重要的影响，在尝试将某负荷加入孤岛时，其同段母线或同一线路分段中的不可控负荷（未装备负荷控制终端的负荷）也将被加入到孤岛范围内，影响孤岛内负荷总量，除此之外，在孤岛划分时，有选择性的关闭一些可控负荷，也可以扩大孤岛范围或更好地满足重要负荷的供电，从而影响孤岛划分结果。

在现有的孤岛划分和孤岛搜索方式中，文献［8，9］介绍了一种基于有序二元决策技术，分阶段在线搜索孤岛区域的方法，但配电网中的DG孤岛与输电系统中的孤岛有所不同［10］。

文献［10］提出的基于有根树的孤岛搜索方法只能应用于辐射状结构的配电网中，不适用于环网结构。

文献［11］将负荷全部处理为可控负荷，在搜索最小生成树的过程中，未考虑同段母线或同一线路分段中的不可控负荷对孤岛内负荷总量的影响。

文献［6］定义了负荷单元的概念，将负荷单元中的全部负荷视为不可控负荷，以负荷单元为单位进行孤岛的扩大融合，未考虑负荷的可控性对孤岛划分的影响。

在保证电力系统安全的前提下，本文根据实际用电的需求，充分考虑负荷管理对孤岛划分的影响，提出了孤岛划分的原则和孤岛划分过程中可能出现的各种约束条件。采用改进的邻接矩阵模型，通过构造支路状态矢量，与关联矩阵结合来反映配电网网架结构的变化，并利用了邻接矩阵连通性的传递性质，实现了对孤岛的拓扑辨识。

1 孤岛划分问题的数学模型

孤岛划分属于非线性、多目标、不可微的约束组合化问题。孤岛划分的约束涉及电气约束、运行条件约束和网络结构约束［12］，并且应考虑系统中重要负荷的用电需求，因此本文在确定孤岛方案时，主要考虑以下两方面的原则：

①在满足孤岛内总负荷不超过DG总发电容量的前提下，使孤岛包含的负荷总量尽可能最大；

②孤岛包含的重要负荷总量尽可能最大。

目标函数考虑划分组合使所有孤岛集合中的负荷单元的负荷加权和最大，即恢复负荷供电率最高。孤岛划分问题的数学描述如下。

目标函数为式中：NL为孤岛内所有负荷节点的集合；SL，k为k节点的负荷总量；λk为k节点的重要系数，对应负荷的等级属性，可根据实际情况设定，λk越大越能体现负荷在目标函数的重要性，有利于该负荷包含于孤岛方案中。如本文算例中重要负荷和一般负荷λk分别取为5和1。

孤岛划分还应考虑电气约束和运行条件约束，其约束条件为

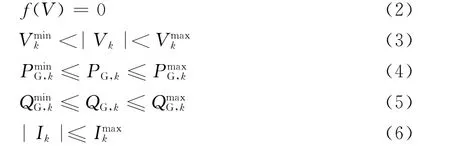
式中：f（V）为潮流平衡方程；Vk为节点k的电压幅值；PG，k和QG，k为节点k发电机总有功／无功出力；Ik为注入节点k的电流。

2 基于邻接矩阵的拓扑描述

邻接矩阵使用节点－支路关联矩阵和支路－节点关联矩阵表示配电网络的基本拓扑结构［13］。图1为一典型配电网接线。

图1 典型的配电网络接线Fig.1 Typical distribution network

把配电网中的电源，母线，用户映射为拓扑图中的节点，节点之间的开关和线路等设备映射为拓扑图中的支路，可得节点－支路的关联矩阵，aij＝1表示节点i与支路j连通，开关全部闭合的矩阵A0称为原始节点－支路关联矩阵。此类关联矩阵包括由其计算得到的邻接矩阵和全连通矩阵皆为布尔型矩阵，遵守布尔运算法则［14］。如果网络中某些开关因故障或其他原因断开，如图1所示，此时对应的节点－支路关联矩阵A称为当前节点－支路关联矩阵。

定义支路状态矢量

支路j正常运行时，sj＝1，因故障或其他原因停运时，sj＝0。

如图1所示，s2＝0，此时有

S＝［101111111］

A就是A0的每一行与S的各个对应元素进行“与”运算后得到的。

显然，也可以定义支路－节点关联矩阵

则有

定义矩阵

则矩阵C表示网络图中节点与节点间的邻接关系。根据连通性的传递性，Cij表示节点i与节点j的连通性，C经过n－1次（n为节点数）自乘可得到全连通矩阵为

T＝C9＝C＾C＾C…＾C＝

根据全连通矩阵T和全连通矩阵行比较法［14］可得到配电网连通区域为（1，3，4，5，6）和（2，7，8，9，10）。

本文通过把实际配电网抽象为拓扑网络，通过定义的节点－支路关联矩阵和支路状态矢量计算得到的全连通矩阵T反映出配电网结构的变化。

3 基于邻接矩阵的含分布式电源配电网的孤岛划分方法

3.1 相关定义说明

（1）可控负荷：安装有负荷控制终端，调度部门可以直接控制（切除或并入电网）的负荷。

（2）不可控负荷：调度部门不能直接控制，只要与电源（变电站或DG）连通，就会被供电的负荷。当孤岛范围发生变化时，必须考虑不可控负荷对负荷总量限制条件的影响。在算法流程中，将同段母线或同一线路分段中的不可控负荷进行合并，并与同段的可控负荷进行关联，只要孤岛中存在与之相关联的可控负荷，此部分不可控负荷也要同时加入到孤岛范围内。

（3）负荷顺序：“负荷顺序”是算法自定义的向孤岛内添加负荷时的搜索顺序。

“负荷顺序”只针对可控负荷而言，不可控负荷是根据与可控负荷的关联关系加入孤岛之中的。“负荷顺序”可以是按可控负荷节点重要性从高到低，重要性相同的负荷按负荷量从大到小的顺序进行排列，也可以根据需求自定义排列，原则上尽可能将同在一个分段或支路的负荷节点排列在一起，靠近DG的分段或支路负荷排列在前，以减少形成孤岛时开关操作次数。

（4）（孤岛内）负荷总量限制条件［12］为

式中：NG为孤岛内DG的集合；β为孤岛内线路损耗所占DG总容量的百分比。

需要注意的是，负荷总量限制条件考虑了孤岛内的线路损耗，所以β及其所确定的负荷总量限制条件都应当在每次潮流计算后相应进行改变。

（5）分离区域：因故障与大电网分离的部分。

（6）计算网络D：算法用于讨论的抽象网络，等同于实时形成的孤岛部分。

（7）配电网的开关位置矢量K：如i支路上有开关设备，则Ki＝1，否则Ki＝0，以图1所示配电网络图为例，此时有

K＝［111100011］

开关位置矢量K用于确定可以动作的开关位置，并可通过相应位置上Ki与Si的异或运算来改变有开关支路的运行状态，即改变支路状态矢量S。

（8）负荷顺序矢量V：按“负荷顺序”对负荷节点进行排序形成负荷顺序矢量V，负荷顺序矢量V可由一定的负荷排序原则动态形成。

3.2 假设条件

本文基于邻接矩阵的含分布式电源配电网的孤岛划分方法主要基于如下假设条件：

①故障前配电网的网架结构和运行情况是已知的；

②故障点、重要负荷和DG的位置是已知的；

③正常运行方式下，DG并网运行；

④故障可以被隔离。

3.3 算法的描述

本文算法在隔离故障后，先确定从大电网分离的包含DG连通区域，以缩小孤岛划分的搜索范围。其次，在满足负荷总量限制条件的前提下，尝试以“负荷顺序”将分离区域内可控负荷与DG连通，并在扩大孤岛的过程中充分考虑不可控负荷的影响。在添加负荷结束后，对各种约束条件进行检查，并对出现的越限情况进行处理，必要时对孤岛内可能引起越限的负荷进行切除。然后重新进行扩大孤岛过程，如此循环直至得到可行的孤岛划分结果，其算法流程见图2。

步骤1 检测故障并隔离故障，确定从大电网分离的区域，以缩小孤岛划分的搜索范围。在故障定位后，得到故障后支路状态矢量S′（S0中动作开关所在支路或断线支路对应的状态矢量S0i＝0得到S），通过第2节所介绍方法，根据原始节点－支路关联矩阵A0与S′的相关计算得到全连通矩阵T并搜索分离连通区域，进而可以得到包含DG的从大电网分离的区域。得到从大电网分离的区域后，建立分离区域的初始节点－支路关联矩阵A0S（不包含故障支路）和分离区域的初始支路状态矢量S0S、开关位置矢量KS、负荷顺序矢量VS，以缩小算法的搜索范围。

步骤2 切除分离区域内所有的可控负荷并将区域内的所有开关断开，初始计算网络D，将分离区域内所有的可控负荷节点的状态置为停运，支路状态矢量为S1S＝S0Sxor KS。

步骤3 尝试扩大孤岛范围，进行添加负荷方案，添加负荷方案是通过现有的开关设备将负荷加入到计算网络D中，添加负荷方案描述如下。

①确定初始计算网络D。尝试连接分离区域中的DG和“负荷顺序”中排序第一的负荷节点VS1。利用邻接矩阵找到DG到VS1节点在分离区域中的最短路径［15］。若将VS1节点加入计算网络D中满足负荷总量限制条件（考虑与之相关联的不可控负荷的影响，下同），则可将此负荷加入，并通过找到的最短路径得到S2S（S1S中最短路径所经支路对应的状态矢量S1Si＝1得到S2S）；否则，不能将此负荷加入计算网络D中，直接转入下一步；

②以“负荷顺序”，尝试将分离区域内的其他负荷节点加入计算网络D：若某负荷节点加入计算网络D中，满足负荷总量限制条件，则可将此负荷加入，并相应更新SkS。将此步骤的SkS全部按顺序保存，以便以后的减负荷方案中进行使用；

③在分离区域中的所有负荷节点均被尝试加入计算网络D后，添加负荷方案结束。

步骤4 添加负荷方案结束后，对形成的孤岛进行潮流计算，对约束条件进行检查。对孤岛系统（计算网络D）进行潮流计算，检查是否存在越限情况（约束条件（2）～（6））：满足约束条件，算法结束得到孤岛划分结果；不满足约束条件，执行约束处理方案

步骤5 对越限的约束条件进行处理。

图2 算法流程Fig.2 Flow chart of the proposed algorithm

①如果孤岛系统存在电压越限的情况：考虑通过DG调压措施处理电压越限，若单独的调压措施不能解决电压越限情况，则执行减负荷方案。b.在减负荷方案切除了可能引起越限问题的负荷后，需要再次进行添加负荷方案（步骤3）并进行潮流计算，如此循环直至得到可行的孤岛划分结果为止。需要注意的是，此后的添加负荷方案过程尝试加入的负荷不包括每次减负荷方案中最后切除的负荷节点。

步骤6 得到可行的孤岛划分方案，输出结果。

根据最后得到的支路状态矢量SkS，通过与分离区域的初始节点－支路关联矩阵A0S进行相应计算得到全连通矩阵Ts，并搜索包含DG分离连通区域，进而可以得到最后的孤岛划分结果。

4 测试系统及计算结果分析

②如果孤岛系统存在其他越限情况，则直接执行减负荷方案来处理越限问题。减负荷方案描述如下：

a.减负荷方案从某种意义上可以说是添加负荷方案的逆过程，目的是将可能引起系统越限问题的负荷切除。以孤岛中后添加的负荷先去除的原则，对计算网络D中的负荷进行切除，并对支路状态矢量SkS进行逆向更新，在切除了越限节点（支路）下游的某一负荷后，此次减负荷方案结束；

在Matlab计算环境下，采用配电网IEEE34节点测试馈线对本文的算法进行仿真计算。相应馈线的参数见文献［16］，网络结构及开关配置情况见图3，测试系统的基本信息见表1。

由文献［16］可知，测试系统将负荷分为点负荷（spot loads）和分布式负荷（distributed loads）。点负荷以节点形式存在，负荷量较大。分布式负荷分布在节点之间，负荷量较小。本文假设系统中所有的点负荷都为重要负荷，分布式负荷均为一般负荷；假设点负荷均为可控负荷，分布式负荷有着相同的可控负荷比例。

在不同的可控负荷比例和“负荷顺序”排列的条件下，对测试配电网系统进行孤岛划分，共制定4种不同的测试方案，见表2。

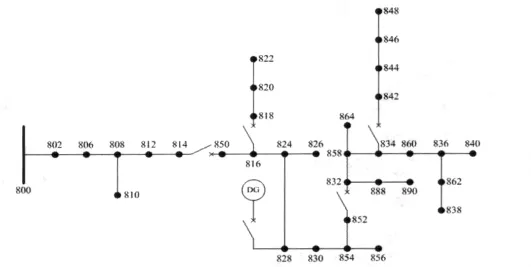
图3 IEEE34节点测试馈线Fig.3 IEEE 34 node test feeder

表1 测试系统基本信息Tab.1 Basic information of test feeder

表2 测试方案描述Tab.2 Description of Test Cases

4种不同的测试方案结果如表3所示。

表3 测试方案描述Tab.3 Description of Test Cases

由仿真过程可知，本文算法可在较短的时间内得到可行的孤岛划分结果。由表3可知，4种方案有相似的孤岛规模，但方案1、4中负荷有着较高的可控比例明显比前两种方案能更好地保证重要负荷的供电（关闭重要负荷总量较小），方案2、4由于采取“就近供电”的原则来制订“负荷顺序”，分别较方案1、3有着更小的线路损耗，在实际算例中，相同的硬件条件下，方案2、4形成可行孤岛所用时间也较方案1、3更少，搜索的速度更快。仿真结果也充分说明有效的负荷管理和得当的“负荷顺序”对形成合理孤岛的重要性。

5 结论

（1）利用邻接矩阵可以实现配电网网架的参数化运算，有利于实现计算机编程。

（2）启发式的搜索策略，首先缩小搜索的空间，然后有所偏好地进行搜索，可避免陷入复杂耗时的全局搜索之中，在较短时间内得到可行的孤岛划分结果。

（3）本文通过对IEEE34节点测试馈线进行测试，表明了本文算法的正确性和有效性，并分析了负荷管理和“负荷顺序”对孤岛划分结果的影响。测试结果证明了负荷管理对孤岛划分的影响，提高系统中负荷的可控比例，能够提高孤岛规模的可控性，更好地满足较重要负荷的供电需求。

［1］ 余贻鑫，栾文鹏（Yu Yixin，Luan Wenpeng）.智能电网述评（Smart grid and its implementations）［J］.中国电机工程学报（Proceedings of the CSEE），2009，29（34）：1－8.

［2］ 鲁鸿毅，应鑫龙，何奔腾（Lu Hongyi，Ying Xinlong，He Benteng）.微型电网联网和孤岛运行控制方式初探（Control strategy for micro－grid in net－connected and islanded operation）［J］.电力系统保护与控制（Power System Protection and Control），2009，37（11）：28－31.

［3］ 施婕，艾芉（Shi Jie，Ai Qian）.智能电网实现的若干关键技术问题研究（Research on several key technical problems in realization of smart grid）［J］.电力系统保护与控制（Power System Protection and Control），2009，37（19）：1－4，55.

［4］ 王建，李兴源，邱晓燕（Wang Jian，Li Xingyuan，Qiu Xiaoyan）.含有分布式发电装置的电力系统研究综述（Power system research on distributed generation penetration）［J］.电力系统自动化（Automation of E－lectric Power Systems），2005，29（24）：90－97.

［5］ IEEE Std 1547，IEEE standard for interconnecting distributed resources with electric power systems［S］.

［6］ 易新，陆于平（Yi Xin，Lu Yuping）.分布式发电条件下的配电网孤岛划分算法（Islanding algorithm of distribution networks with distributed generators）［J］.电网技术（Power System Technology），2006，30（7）：50－54.

［7］ 王明俊（Wang Mingjun）.市场环境下的负荷管理和需求侧管理（Load management and demand side management in electricity market environment）［J］.电网技术（Power System Technology），2005，29（5）：1－5.

［8］ Zhao Qianchuan，Sun Kai，Zheng Dazhong，et al.A study of system splitting strategies for island operation of power system：a two－phase method based on OBDDs［J］.IEEE Trans on Power Systems，2003，18（4）：1556－1565.

［9］ Sun Kai，Zheng Dazhong，Lu Qiang.Splitting strategies for islanding operation of large－scale power systems using OBDD－based methods［J］.IEEE Trans on Power Systems，2003，18（2）：912－923.

［10］丁磊，潘贞存，从伟（Ding Lei，Pan Zhencun，Cong Wei）.基于有根树的分布式发电孤岛搜索（Searching for intentional islanding strategies of distributed generation based on rooted tree）［J］.中国电机工程学报（Proceeding of the CSEE），2008，28（25）：62－67.

［11］董晓峰，陆于平（Dong Xiaofeng，Lu Yuping）.基于改进Prim算法的分布式发电孤岛划分方法（Islanding algorithm for distributed generators based on improved prim algorithm）［J］.电网技术（Power System Technology），2010，34（9）：195－201.

［12］Mao Yiming，Miu K N.Switch placement to improve system reliability for radial distribution systems with distributed generation［J］.IEEE Trans on Power Systems，2003，18（4）：1346－1352.

［13］张伟，周步祥（Zhang Wei，Zhou Buxiang）.基于有向支路的配电网络拓扑分析方法（Topology analysis method of distribution network based on vector branch）［J］.电力系统自动化（Automation of Electric Power Systems），2004，28（22）：38－41，82.

［14］梁洪（Liang Hong）.配电网拓扑分析方法研究（Studies on Topology Analysis of Distributed Networks）［D］.成都：电子科技大学计算机科学与工程学院（Chengdu：School of Computer Science and Engineering University，E－lectronic Science and Technology），2008.

［15］吕昊，付立军，叶志浩，等（LüHao，Fu Lijun，Ye Zhihao，et al）.几种电力网络图的连通路径拓扑算法研究（Some topology algorithm research of power network connectivity path）［J］.电力系统保护与控制（Power System Protection and Control），2009，37（21）：82－85.

［16］Distribution System Analysis Subcommittee.IEEE 34 Node Test Feeder［R］.Piscataway：IEEE Power Engineering Society，2004.