改进的人工鱼群算法设计次同步阻尼控制器

邓盼盼，李兴源，王渝红，穆子龙，顾 威

（四川大学电气信息学院，成都 610065）

与交流输电相比，高压直流输电HVDC（high voltage direct current）具有高度可控、调节迅速、传输功率大、运行灵活等特点，在远距离大容量输电、区域电力系统互联等方面有其优越性。目前，直流输电因其在经济和技术上的优势，在远距离大容量输电和大区联网两个方面得到广泛应用［1，2］。但是另一方面，HVDC系统的快速可控，存在着与汽轮发电机组轴系机械系统发生次同步扭振相互作用的可能性，这是一个需要重点关注的问题。

次同步振荡SSO（subsynchronous oscillation）是指汽轮发电机组在运行平衡点受到扰动后处于特殊运行状态下出现的一种异常状态，在这种运行状态下，电气系统与汽轮发电机组之间在一个或多个低于系统同步的频率下进行显著的能量交换［3］。

在以往针对次同步振荡的研究文献中，通过各种方法设计控制器实现了对振荡的抑制［4～6］。但一般方法设计出的控制器难以达到最好效果，且往往是针对某一运行情况，控制器参数固定。人工鱼群算法AFSA（artificial fish swarm algorithm）拥有自学习、互学习能力，善于处理多维多目标问题，特别适用于非线性系统，并具有较好的鲁棒性，但易陷入局部最优值。

本文通过对人工鱼的觅食行为、聚群行为、追尾行为和行为选择进行了分析、改进，使得AFSA算法得到改善。并基于此改进算法，以四川电网向家坝－上海直流输电系统的送端为研究对象，设计了次同步阻尼控制器SSDC（subsynchronous damping controller），以达到抑制SSO的目的。

1 AFSA算法及其改进

1.1 AFSA算法

鱼行动的特点就是自行或尾随其他鱼找到营养物质多的地方，因而鱼生存数目最多的地方一般就是本水域中营养物质最多的地方［7］。AFSA算法就是根据这一特点，通过构造人工鱼来模仿鱼群的觅食、聚群及追尾行为，从而实现寻优［8］。

以求极小值问题为例，在一个n维的目标搜索空间中构造m条人工鱼组成一个鱼群，第条人工鱼的位置可以用向量xi＝［xi1xi2… xin］表示，其在当前位置的食物浓度即适应度函数为Y＝f（x）。人工鱼的感知距离即视野用V表示，人工鱼在运动过程中感知其视野范围内其他鱼的状况从而决定自己的行为选择。拥挤度因子用δ描述，表示在某个位置附近的拥挤程度，取0＜δ＜1。人工鱼的典型行为有觅食、追尾和聚群［9］，以下分别进行介绍。

1.1.1 追尾行为

设人工鱼当前状态为xi，探索视野范围内的人工鱼中Yi为最小的伙伴xj。如果xj的状态具有较高的食物浓度并且其周围不太拥挤，则朝伙伴xj的方向前进一步；否则执行觅食行为。

1.1.2 觅食行为

当前人工鱼xi，在其视野范围内随机选择一个状态量xj，如果适应度函数Yj＜Yi，则向该方向前进一步，前进步长step的方向与向量xixj同向。反之，再重新随机选择状态xj，判断是否满足前进条件；反复几次后，如果仍不满足前进条件，则随机移动一步。

1.1.3 聚群行为

当前人工鱼xi，探索当前视野内的伙伴数目nf及其中心位置xc，如果Yc／nf＞δYi，表明伙伴中心位置有较多的食物并且不太拥挤，则朝中心位置向前进一步。

在AFSA中，设置一个公告板，用以记录当前所有人工鱼中最佳状态及该状态的食物浓度。各人工鱼每次行动完毕后，将最新位置的食物浓度与公告板中的食物浓度进行比较，如果该位置的食物浓度大于公告板中的食物浓度，则用该位置及其食物浓度代替公告板中的相应值。

1.2 改进AFSA算法

通过对AFSA算法的研究，发现视野范围较大，人工鱼的全局搜索能力强并快速收敛，但精度差；视野范围较小，人工鱼的局部搜索能力强，但易陷入局部最优值。步长大，收敛速度快，但有时会出现振荡现象；步长小，收敛速度慢，但求解精度高。

根据AFSA算法的性质，调整视野V和步长step公式为

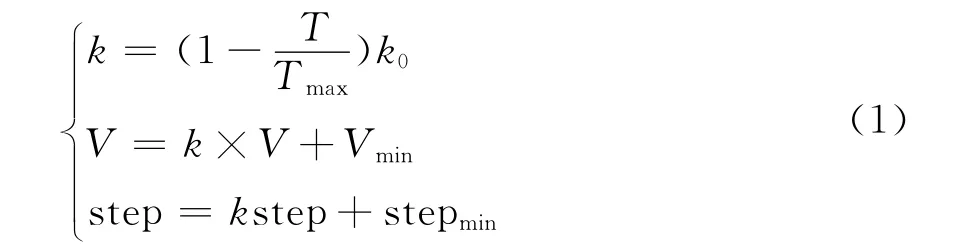
式中：T为当前迭代次数；Tmax为最大迭代次数。

如式（1）所示，应先使视野V和步长step有一较大初始值，以便于进行全局搜索。而随着迭代次数的增加，应逐步减小V和step的值。在算法运行后期，逐步加强局部搜索，定位在最优解附近区域并进行精细搜索，从而在保证收敛速度的基础上提高了算法的局部搜索能力和寻优结果的精度。

在觅食行为中，人工鱼随机选择一个状态，如果该状态优于当前位置，没有必要向该方向移动一步，为了加快搜索速度，人工鱼可以直接移动到该位置。反复几次后，如果仍不满足前进条件，则原地不动，而不是随机移动一步。另外，可以通过调控觅食行为中的重复尝试次数，防止结果陷入局部极值。为限制盲目聚群，对nf的值做出限制：当前人工鱼xi，探索当前视野内的伙伴数目，当nf＞2时，才进行是否聚群判断。

整个算法的行为选择顺序可以调整为觅食、追尾、聚群。人工鱼的初始状态都是随机的，首先尝试觅食，可使每条人工鱼均有较好的状态后，再进行追尾和聚群。这样避免了盲目的追尾、聚群行为，有效提高了算法的收敛速度。

2 系统模型

四川是一个电力输出大省。根据2012年四川电网丰水期大方式规划数据，四川电网全口径装机容量37357 MW。到2012年，川南将建成向家坝－上海和锦屏－苏南两回±800 k V特高压直流输电线路。其中向上直流送端换流站落点集中的交直流混合输电系统稳定性问题成为亟待研究与解决的重点，其拓扑结构如图1所示。

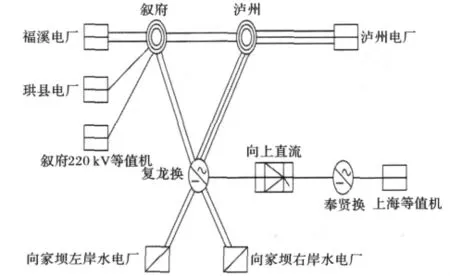
图1 拓扑结构Fig.1 Topology structure

本文以PSCAD／EMTDC作为软件平台，建立如图1所示的电磁暂态模型，研究各种孤岛运行方式下，向上直流输电系统与其送端临近大型火电机组的次同步振荡特性。根据仿真结果，向上直流降功率至20%的运行方式中，泸州机组次同步振荡情况比较严重，可能会对机组的轴系造成疲劳积累，缩短发电机轴系的寿命。

3 SSDC抑制SSO的原理

直流系统引起次同步振荡的根本原因是其快速控制导致系统产生负阻尼。美国电力研究院EPRI（Electric Power Research Institute）首先提出了用SSDC来抑制直流系统次同步振荡，其基本原理就是在次同步频率范围内为汽轮发电机提供合适的正阻尼。根据EPRI报告中SSDC的设计思路［10］，将SSDC装设于直流系统的整流器控制侧，然后通过经典控制理论中的超前、滞后校正补偿在所需要频率处的相位，可以有效增加系统次同步频率段的电气阻尼，从而抑制由直流输电系统引起的次同步振荡。如图2所示，就是希望增加的SSDC回路能够提供合适的阻尼转矩，使电磁阻尼De为正值，以达到抑制次同步振荡的目的。

对于次同步阻尼控制器的设计而言，输入信号的选择需要遵循两个原则，一是可实现性，二是有效性［11］。为了实现本地可测量，及足够的灵敏度，本文采用换流站高压交流母线的频率偏差信号ΔfHLZ，作为所设计的直流附加控制器SSDC的输入信号。四阶带通滤波器的频带为5～45 Hz。惯性环节、相位校正环节以及比例增益环节中的参数K、T1、T2、T3为自适应参数，将利用改进的AFSA算法得到。

图2 HVDC附加SSDC的基本原理Fig.2 Basic principle of HVDC added SSDC

4 基于改进的AFSA算法设计SSDC

4.1 设计思路

建立适应度函数前应先导出全系统的状态方程。先确定多馈入直流与交流混合系统各元件的数学模型，包括机组发电机的转子运动方程、轴系方程、励磁绕组的电磁暂态方程、电力系统稳定器的方程、直流系统控制器的方程和直流输电系统的方程，据此可得全系统状态方程为

式中：X为状态变量，X＝［ΔωiΔδiΔE′qΔEfΔV1ΔVSΔI1ΔISΔPdc］T；U为控制变量，U＝［ΔVISΔfHLZΔudc］T。ΔVIS、ΔV1、ΔVS分别为PSS控制器的输入变量、中间量、输出变量；ΔfHLZ、ΔI1、ΔIS分别为SSDC控制器的输入变量、中间量、输出变量；ΔPdc＝PdcREF－Pdc，PdcREF为直流功率的给定值，Δudc为直流功率的控制输入信号。

安装SSDC的目的是在复平面上让次同步振荡模式相应的特征根向左移动。系统特征值为

特征值的实部给出了系统阻尼，虚部给出了系统的振荡频率。负实部表示阻尼振荡，正实部表示增幅振荡。由此定义阻尼比

系统阻尼比确定了振荡幅值的衰减速度。SSDC应针对机组不稳定的扭振频率，使该振荡模态的特征值实部最大限度地往复平面左移，即要求阻尼比越大越好。因此，要使次同步振荡模态的阻尼比最大化，应将适应度函数选定为阻尼比。适应度函数为

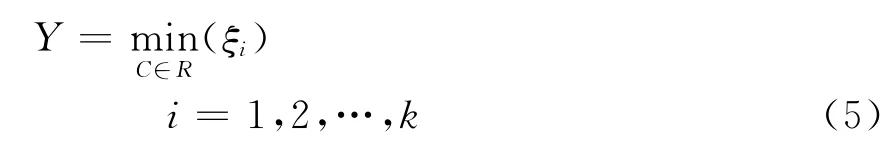
式中：ξi为第i个机电振荡模态的阻尼比；C为系统的运行条件；R为所有可能运行条件的集合。

因此，利用改进的AFSA算法进行SSDC的设计，首先应通过选定的控制器自适应参数构造人工鱼来模仿鱼群的觅食、聚群及追尾等行为，以阻尼比作为适应度函数来比较各条人工鱼的状态，从而实现寻优。这样SSDC的设计问题就转化为阻尼比寻优的问题。

4.2 算法流程

步骤1 初始化人工鱼群规模，将鱼群的规模设定为m＝10，搜索空间维数定为N＝4，每一条人工鱼的元素分别代表变量K、T1、T2、T3；初始化视野V和步长step、拥挤度δ、最大重复尝试觅食次数trynumber、最大迭代次数等参数。

步骤2 按式（1）计算视野V和步长step。步骤3 每个个体依次进行觅食、追尾和聚群行为。

步骤4 根据每一条人工鱼的当前状态，即K、T1、T2、T3代入状态方程，解出特征值，再将特征值代入适应度函数，计算出每条人工鱼所对应的适应值，并将其适应值与公告板进行比较，若较好，则将其赋给公告板。

步骤5 检查终止条件。（达到预定迭代次数或足够好的适应值），如果满足终止条件，则输出最优解（公告板中人工鱼状态和函数值），算法终止；否则，转入步骤2。

5 仿真分析

以次同步振荡最严重的向上直流降功率至20%的运行方式为例，针对泸州机组固有扭振频率：13.6 Hz，25.6 Hz，30.7 Hz，首先采用Prony辨识泸州机组的次同步振荡模态。

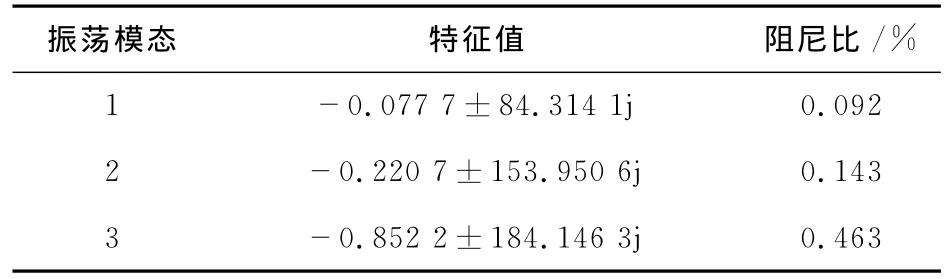
表1 次同步振荡模态Prony辨识分析Tab.1 Prony identification analysis for SSO modal

从表1中可以看出，有三个振荡模态，其中模态1特征值实部接近于零，属于不稳定状态，系统在受到扰动后，容易激发次同步振荡。

然后将采用遗传算法GA（genetic algorithm）设计出的SSDC，以及采用改进AFSA算法得到的SSDC加到向上直流整流侧控制系统中，对系统重新进行Prony辨识，结果如表2和表3所示。

表2 加入GA算法SSDC后次同步振荡模态Prony辨识分析Tab.2 Prony identification analysis for SSO modal with SSDC of GA

表3 加入改进的AFSA算法SSDC后次同步振荡模态Prony辨识分析Tab.3 Prony identification analysis for SSO modal with SSDC of improved AFSA

从表2与表3的对比中可以看出，加入了SSDC以后，各个模态下的特征值实部均往复平面左移，阻尼比也明显增大。但是使用了改进的AFSA算法设计的SSDC与使用遗传算法设计出的SSDC相比，能够使各个模态下的特征值实部更大限度地往复平面左移，相应的阻尼比也更好。

同时，针对这一运行方式，采用时域仿真来验证用GA算法设计出的SSDC，以及采用改进AFSA算法得到的SSDC对次同步振荡的抑制作用。机组模型中均采用4质量块的轴系模型，分别为高中压缸（HIP）、低压缸A（LPA）、低压缸B（LPB）和发电机缸（GEN）。取故障为2 s时泸州到复龙换流站，1回线单相接地故障，0.1 s后恢复。仿真结果如图3～图5所示。

由图4和图5可以看到，加入了SSDC以后，轴系的扭振均呈衰减趋势。但是使用了改进的AFSA算法的SSDC比使用遗传算法设计出的SSDC能在更短的时间内使扭矩衰减至稳定值，使得系统能够更快进入稳定运行状态，同时也保证了汽轮发电机组轴系的安全。并且在加装针对泸州机组设计的SSDC后，对福溪、珙县机组的扭振相互作用现象，也有一定的抑制作用，如图6和图7所示。

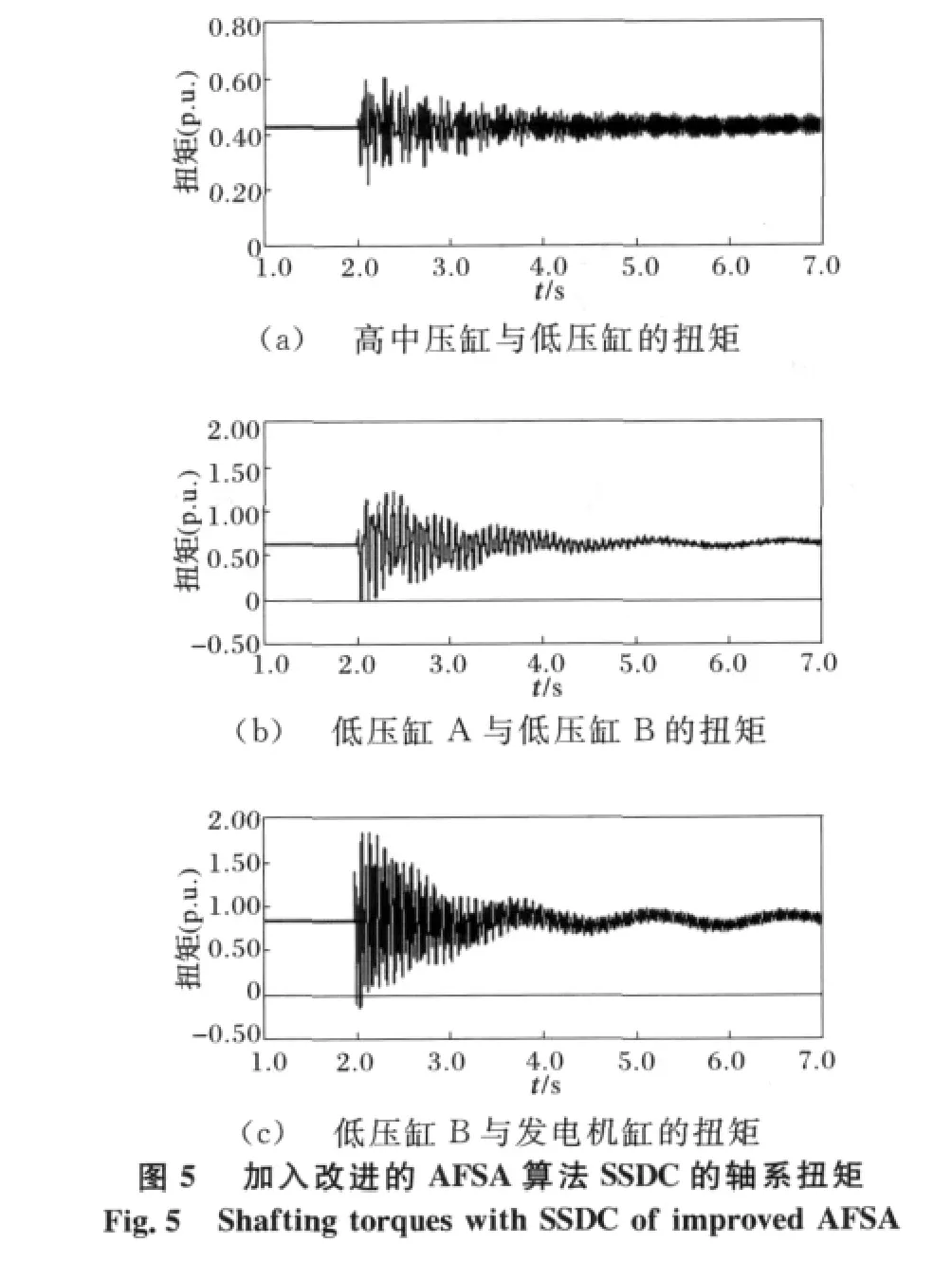
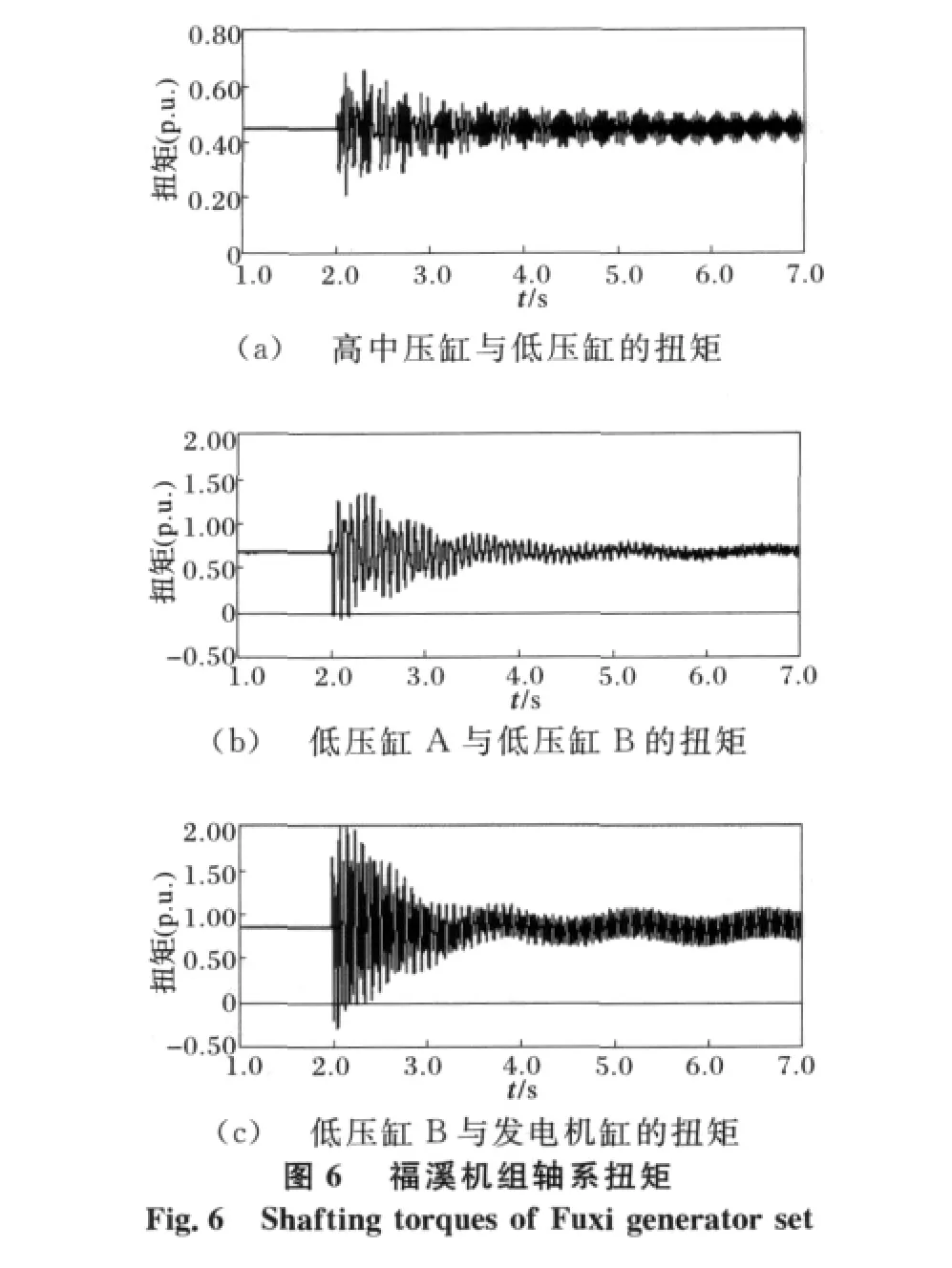
图7 珙县机组轴系扭矩Fig.7 Shafting torques of Gongxian generator set

6 结语

本文提出的改进AFSA算法较好地平衡了全局搜索能力和局部搜索能力，收敛迅速且不易陷入局部最优值，提高了该算法的自适应能力和优化精度。基于改进的AFSA算法，进行了次同步阻尼控制器的设计。通过Prony辨识分析和PSCAD／EMTDC的电磁暂态仿真证明了该次同步阻尼控制器能有效抑制轴系扭振，且具有时间短、具有一定鲁棒性的特点。

［1］ 李兴源.高压直流输电系统的运行［M］.北京：科学出版社，1998.

［2］ 浙江大学发电教研组直流输电科研组.直流输电［M］.北京：电力工业出版社，1982.

［3］ 程时杰，曹一家，江全元.电力系统次同步振荡的理论与方法［M］.北京：科学出版社，2009.

［4］ 伍凌云，李兴源，龚勋，等（Wu Lingyun，Li Xingyuan，Gong Xun，et al）.基于模糊免疫方法的次同步阻尼控制器设计（Design of subsynchronous damping controller based on fuzzy immune method）［J］.电力系统自动化（Automation of Electric Power Systems），2007，31（11）：12－16.

［5］ 刘振亚.特高压直流输电技术研究成果专辑（2005年）［M］.北京：中国电力出版社，2006.

［6］ Svensson S，Mortensen K.Damping of subsynchronous oscillations by an HVDC link an HVDC simulator study［J］.IEEE Trans on Power Apparatus and Systems，1981，100（3）：1431－1439.

［7］ 班晓娟，艾冬梅，陈泓娟，等.人工鱼［M］.北京：科学出版社，2007.

［8］ 李晓磊，邵之江，钱积新（Li Xiaolei，Shao Zhijiang，Qian Jixin）.一种基于动物自治体的寻优模式：鱼群算法（An optimizing method based on autonomous animals：fish－swarm algorithm）［J］.系统工程理论与实践（Systems Engineering Theory ＆Practice），2002，22（11）：32－38.

［9］ 李晓磊，冯少辉，钱积新，等（Li Xiaolei，Feng Shaohui，Qian Jixin，et al）.基于人工鱼群算法的鲁棒PID控制器参数整定方法研究（Parameter tuning method of robust PID controller based on artificial fish school algorithm）［J］.信息与控制（Information and Control），2004，33（1）：112－115.

［10］Piwko R J，Larsen E V.HVDC system control for damping of subsynchronous oscillations［J］.IEEE Trans on Power Apparatus and Systems，1982，101（7）：2203－2211.

［11］周铁强，刘福生（Zhou Tieqiang，Liu Fusheng）.高压直流输电系统次同步振荡的几种研究方法及其对比分析（HVDC system subsynchronous resonance several researching method and comparing analysis）［J］.电力系统及其自动化学报（Proceedings of the CSUEPSA），1992，4（2）：32－40.