基于均值漂移和粒子滤波相结合的水下运动目标跟踪

雷 飞，张新颖，王 依

LEI Fei1,ZHANG Xin-ying1,WANG Yi2

（1. 北京工业大学 电子信息与控制工程学院，北京 100124；2. 东北石油大学 研究生院，大庆 163318）

0 引言

水下智能监控系统对保证游泳者生命安全起着至关重要的作用，而实时的运动目标跟踪是其中关键的步骤。由于水下环境与其他自然场景不同，它受到光照、水波、倒影等的影响，是一个动态场景，且游泳者是非刚性目标，因姿态的变化目标会发生形变，这些都给水下的运动目标跟踪带来很大困难。因此水下视频监控中的目标跟踪算法既要适应目标和背景的复杂变化，又要保证快速、稳定的实时跟踪目标。

近年来，研究人员提出了很多目标跟踪算法，如基于特征的跟踪，基于区域的跟踪和基于变形模型的跟踪等。其中均值漂移（Mean Shift）算法[1]是一种基于密度梯度上升的非参数方法。其计算量小，适合于实时跟踪场合。粒子滤波（Particle Filter）为解决非高斯、非线性系统的目标跟踪提供了有效的手段。它通过在状态空间中传播的随机样本的概率密度去逼近目标状态的后验概率密度，从而达到最优贝叶斯估计。该方法不受动态系统各 个随机量分布形式的限制，有效地克服了卡尔曼滤波的缺点，能够应用于非线性、非高斯的运动系统中。例如Isard[2]等人利用粒子滤波算法跟踪连续图像序列中的目标轮廓；Dallert[3]等将粒子滤波和移动机器人运动和感知的概率模型相结合，提出了移动机器人蒙特卡罗定位的思想；Okuma[4]等通过将自提升检测与粒子滤波方法相结合实现了多目标的自动初始化及跟踪。

但是以上算法都是针对背景相对简单的室内监控，或者运动目标的形状具有一定规律性的情况，暂未见有关水下复杂背景下的运动目标跟踪算法。

本文结合Mean Shift算法中的核函数原理和目标模型，以RGB颜色直方图为核心建立水下运动目标模型，采用粒子滤波算法实现水下运动目标跟踪，并在跟踪过程中利用Mean Shift收敛粒子。该方法融合了Mean Shift良好的实时性和粒子滤波的鲁棒性。仿真试验结果表明，该算法能够克服气泡、倒影、遮挡的影响，实现稳定、快速的目标跟踪。

1 Mean Shift算法

Mean Shift是一种基于核密度估计的处理方法。给定一组n个一维空间的数据点的集合S＝，它的未知的概率密度函数为f (x)，取核函数Kh(x)，则在x点处的密度可按下式计算：

核密度函数估计的含义可以解释为：将在每个采样点为中心的局部函数的平均效果作为该采样点概率密度的估计值。

由于水下目标是非刚性物体，其会随着游泳姿势的改变而发生形变，而利用颜色特征具有尺度、旋转和平移不变性，因此采用颜色直方图作为目标的特征具有很好的稳定性。本文结合Mean Shift算法中提到的核函数的概念，利用RGB颜色直方图建立水下运动目标模型。核函数选择Epanechikov Kernel，即：

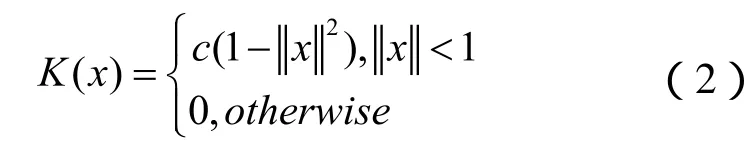
设目标区域的中心为x0，区域内的像素点用{xi; i=1,2,,N}表示。将RGB每个颜色通道划分为n个区间，则颜色的特征值u＝1,2,,M，M＝n3。按照下面公式建立模型：

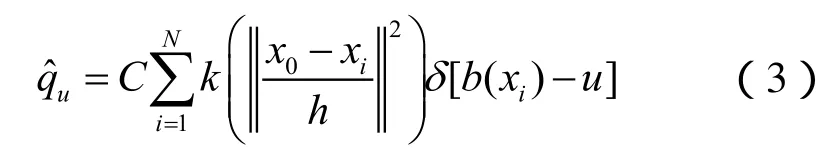
其中，d是Delta函数，C是常量系数使得

计算得到

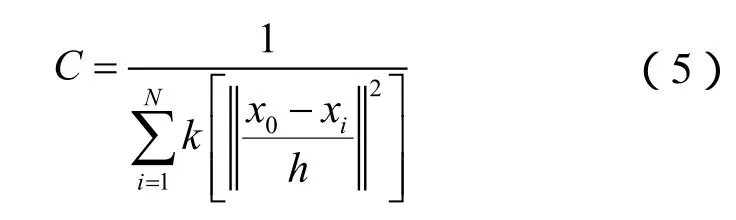
同理，以每个粒子为中心的候选目标模型为：

本文提出的跟踪算法需要计算初始帧中目标的颜色直方图作为模板，粒子区域的颜色分布与目标颜色分布越相似，权值越大，反之越小。本文使用Bhattacharyya系数作为度量直方图之间相似性的函数：

Bhattacharyya距离为：

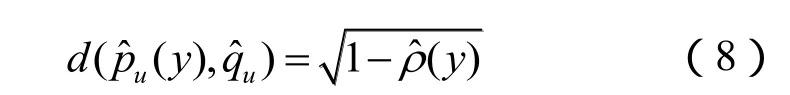
要使式（9）取得最大值，需要计算Mean Shift向量，通过迭代使其第二项取得最大值[5]。由于Mean Shift的收敛性，在不断的迭代中，候选目标的中心y0会移动到新位置yi：

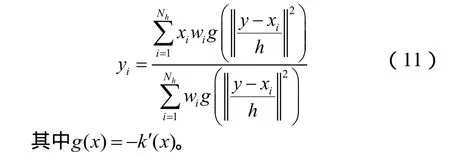
2 粒子滤波算法

2.1 粒子滤波原理

粒子滤波作为一种求解贝叶斯概率的实用方法又称为蒙特卡罗方法（Sequential Monte Carlo methods），它利用状态空间中的一系列随机样本（粒子）的加权和表示当前时刻的后验概率密度。当粒子数目不断增大时，所得的离散概率表示逐渐接近其真实值，理想情况下可以看作是最优估计。

假设系统的状态变化模型和观测模型如下：

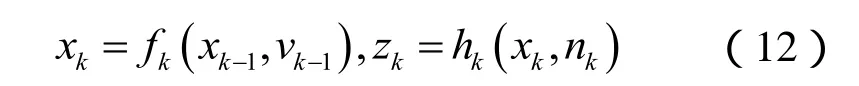
其中，xk表示系统状态变量，vk表示系统噪声，zk表示系统观测值，nk表示观测噪声。状态概率密度分布可用如下经验概率分布近似表述：

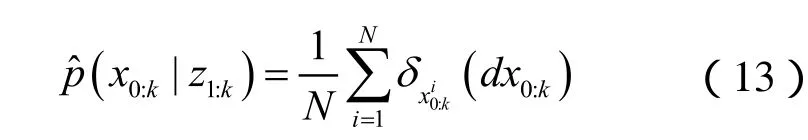
在实际中除了少数满足高斯、均匀分布的系统外，对于大部分非标准分布的函数进行采样是不可能的，通常要借助一些采样算法。实际中多采用实现递推估计的序贯重要性采样(SIS)算法。在SIS算法中，重要性函数是概率分布与p (xk|z1：k)相同，概率密度分布q (x0：k|z1：k)已知并且容易从中采样的分布函数。

若将重要性函数q (x0：k|z1：k)展开成如下连积形式：

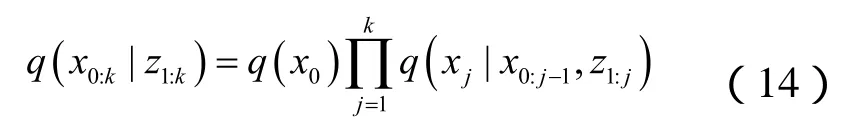
并假设系统满足马尔科夫过程，通过推导得到权值的递推更新公式：

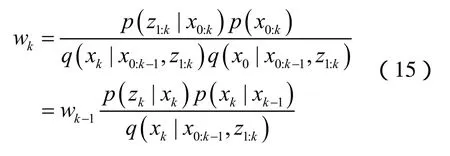
更新概率密度函数为

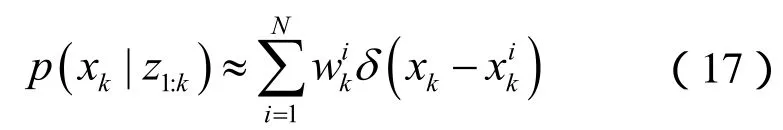
其中

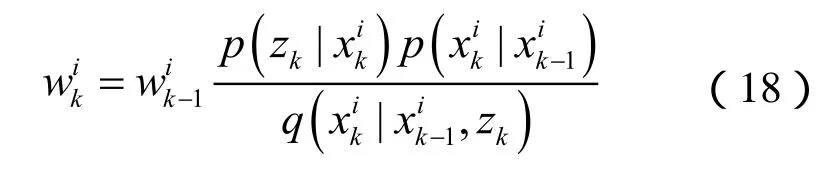
对权值归一化后：

2.2 重要性函数选取

对于SIS粒子滤波器而言，其最大的缺陷就是粒子退化现象[6]，即随迭代的深入，大部分粒子的权值变得很小，只有少数粒子具有较大权值，其多样性逐渐减低。解决这个问题的方法之一是选择合适的重要性分布。

选取重要性函数的准则是使重要性权值的方差最小。Lliu[7]在其文献中证明了采用q (xk|x0：k-1,z1：k)＝ p (xk|x0：k-1,z1：k)作为重要性函数可以获得最优估计的效果，但却需要存储之前所有时刻的状态信息，在实际中，为了计算简单，本文选取q(xk|x0：k-1,z1：k)＝ p (xk|xk-1)作为重要性函数。

2.3 重采样过程

重采样是解决粒子退化问题的另一个有效的方法。本文采用随机采样的方法，其过程是：

1）产生n个在[0，1]上均匀分布的随机数[ml;l=1,2,,n]。

2）通过搜索算法找到满足以下条件的整数m，使得

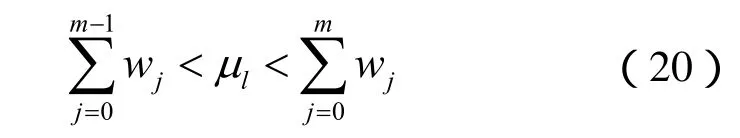
4）将区间[0，1]按式（21）分成n个小区间，当随机数ml落在第m个区间Im=(lm-1,l)上时，对应的样本将进行复制。

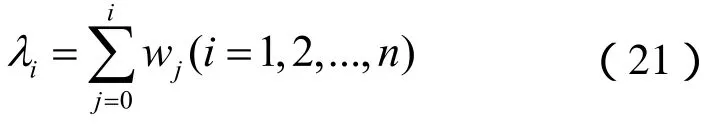
3 水下运动目标跟踪算法步骤

本文以RGB颜色直方图为核心建立水下运动目标模型，并在粒子滤波跟踪水下目标的过程中，通过Mean Shift算法对粒子进行收敛，使粒子的分布更加接近目标真实的位置。具体算法步骤如下：

1） 初始化阶段：

首先在水下视频图像的第一帧中手动选取目标，建立以RGB颜色直方图为核心的参考目标模型，生成粒子集，并令其权重为N-1。

2） 根据状态转换方程，用k-1时刻的粒子集去预测k时刻每个粒子的状态，得到新的粒子位置

3） 根据式（11），通过 Mean Shift算法对粒子在传播半径的邻域内进行迭代，使其收敛到邻域内的最大值，得到新的粒子状态。

4） 更新粒子：

由每个粒子的候选区域与参考目标模型之间的巴氏距离，得到观测值的概率密度函数：

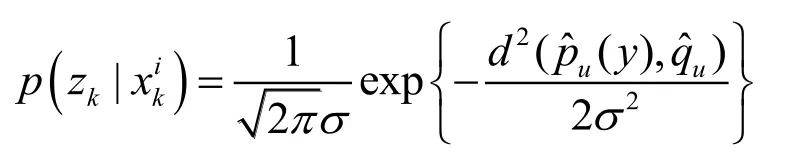
其中s表示均方差。Bhattacharyya 距离越小，相似性越大，粒子所分配的权值也越大。因此，k时刻粒子的权值就可以更新为：

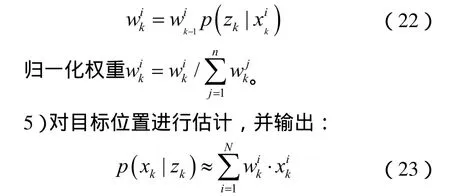
6） 重采样：

7） 令 k=k+1，重复（2）～（6）。

算法流程如图1所示。

4 试验结果与分析

仿真试验中用于跟踪的视频序列共350帧图像，图片尺寸为352×288，色彩深度为 24位。

在本文提出的水下运动目标跟踪算法中，观测值的概率密度函数为

图1 水下运动目标跟踪流程

取s=0.2，重要性函数采用均值为0，方差为1的标准正态函数。在以目标中心为中心，长度为30、宽度为20的矩形区域内进行跟踪。

卡尔曼滤波是目前比较流行的目标跟踪算法之一，其计算量小，预测具有无偏、稳定和最优的特点，但其无法适用于非线性系统中。为了验证本算法的有效性，实验中将本文采用的算法与目前常用的卡尔曼滤波算法[8]进行了比较。

图2是原始视频图像，反应了水下视频图像中的运动目标受到气泡、倒影、浮标对人的遮挡等影响。

图2 原始视频图像

图3是利用Kalman滤波器进行目标跟踪的结果。由于跟踪过程中受到水波、倒影和浮标遮挡的影响，且目标做非线性运动，导致卡尔曼滤波器无法有效的跟踪到目标。从图中可以看出跟踪结果失真严重，到279帧时，完全丢失目标，跟踪失败。

图4是采用本文提出的算法进行水下目标跟踪的结果。在跟踪初期，第17 帧的跟踪结果与图3中的17帧相比，没有表现出明显优势；但随时间的推移，目标受到水波、浮标遮挡、气泡等的干扰，分别如图4中第46帧、第124帧、第185帧和第225帧所示，本文采用的算法依旧能准确地跟踪目标。在第279帧，目标受到自身倒影的影响，采用卡尔曼的跟踪方法已经失效，而本文的算法则表现出了良好的跟踪效果。

图3 利用Kalman滤波器进行目标跟踪的结果

5 结论

本文将Mean Shift和粒子滤波相结合实现了水下运动目标跟踪算法。粒子滤波器的主要缺点是需要大量的粒子来近似描述目标的状态，因而较费时。而本文中利用Mean Shift算法在重采样之前将粒子收敛到靠近目标真实状态的区域内，由于每个粒子表示的状态更加合理，因而算法对粒子数量的需求大大降低，算法的实时性得到了提高。由仿真试验结果可以看出，本文提出的水下运动目标跟踪算法在背景混乱和发生目标遮挡的情况下实现了快速、稳定的实时目标跟踪。进一步地，该算法有效地克服了卡尔曼滤波器的缺点，可以适用于非线性、非高斯的运动系统中。

[1] Cheng Y. Mean shift,mode seeking and clustering [J].IEEE Transactions on Pattern Analysis and Machine Intelligence,1995,17(8)： 790-799.

[2] Isard M,Blake A. Condensation-conditional Density Propagation for Visual Tracking [J]. Int J of Computer Vision,1998,29(1)： 5-28.

[3] F Dellaert,W Burgard，D Fox. “Monte Carlo localisation for mobile robots” in Proceedings of the IEEE International Conference on Robotics and Automation,vol.2 Detroit,MI,May 1999,1322-1328.

[4] Okuma. K.,Taleghani,A.,de Freitas,J.,et al. A Boosted Particle Filter： Multi-target Detection and Tracking. In：European Conference on Computer Vision,2004,1(5)： 28-39.

[5] D. Comaniciu,V. Ramesh,and P. Meer. Kernel-based object tracking[J]. IEEE Trans. on Pattern Analysis and Machine Intelligence,2003,(25)5： 564-577.

[6] 康健,芮国胜. 粒子滤波算法的关键技术应用[J]. 火力与指挥控制,2007(4)： 53-55.

[7] Liu J S,Chen R. Sequential Monte Carlo methods for dynamical systems [J]. J of the American Statistical Association,1998,93(5)： 1032-1044.

[8] Lei fei,Zhao Xiaoxia. Adaptive Background Estimation of Underwater Using Kalman-Filtering[C]. The 3rd International Congress on Image and Signal Processing.16-18 Oct. 2010： 64-67.