在共轭基础上的准双曲面齿轮主动修形设计

邓效忠，蒋 闯

(河南科技大学机电工程学院，河南洛阳471003)

0 前言

准双曲面齿轮由于传动比大、传动平稳、体积小而被广泛应用于汽车的驱动桥主传动中。对于准双曲面齿轮小轮的加工设计，传统的方法是通过局部综合法计算出小轮的机床调整参数［1－4］，然后在专用铣齿机上进行切齿加工。这种方法计算量很大，并且不易得到一套精确的加工参数。精锻近净成形准双曲面齿轮是一项新技术，精锻的模具需要在加工中心上用指形铣刀铣削成形，利用主动设计修形技术对精锻的模具进行加工设计至关重要。基于共轭齿面的主动设计修形技术，与传统切削方式相比，不受刀具和机床结构的限制，根据已得到的大轮齿面，利用共轭齿面原理包络出小轮齿面，再对小轮齿面进行修形，从而达到修正接触区的目的。

在共轭齿面主动修形设计的研究方面，文献［5－6］在理论方面对准双曲面齿轮加以推理计算，但需要确定被计算齿面的一阶及二阶参数;文献［7］利用载荷－变形效应条件来控制弧齿锥齿轮的二阶接触参数，但没有对准双曲面齿轮进行研究。

本文基于大轮成形法加工对齿面点求解，根据啮合坐标系和共轭原理，利用齿面旋转投影原理计算出小轮的三维坐标点和单位法矢［8］。采用抛物线的修形方式对小轮齿面进行修形，在四轴联动的加工中心上进行切齿试验，并在齿轮测量中心上对其进行测量，验证齿面主动修形技术的可行性。

1 共轭齿面点的计算

建立齿轮副啮合坐标系如图1所示。坐标系S1和S2分别与小、大轮固连，Sh与齿轮箱体固连，Sd与Sh固连，为描述大小轮位置关系的辅助坐标系。Sd与Sh的坐标原点Od与Oh分别与大轮和小轮轴线上交叉点重合。φ1和φ2分别为小轮和大轮的啮合转角，E为小轮偏置距，Γ为齿轮副轴线交角(文中为90°)。

图1 齿轮副啮合坐标系

2 共轭齿面修形

本文对齿面点的修形，在齿长方向和齿高方向均采用抛物线型修形方式，基于抛物线修形建立的修形坐标系如图2所示。

坐标系S1是与小轮固连的坐标系，以设计交叉点为原点，X1轴为小轮旋转轴。坐标系Sm为抛物线修形坐标系，坐标原点为小轮节锥线与齿宽中线的交点，以节锥线所在方向为Xm轴，齿面中点的法矢所在的方向为Ym轴，垂直于节锥线的方向为Zm轴。图2中，δ2为小轮节锥角。

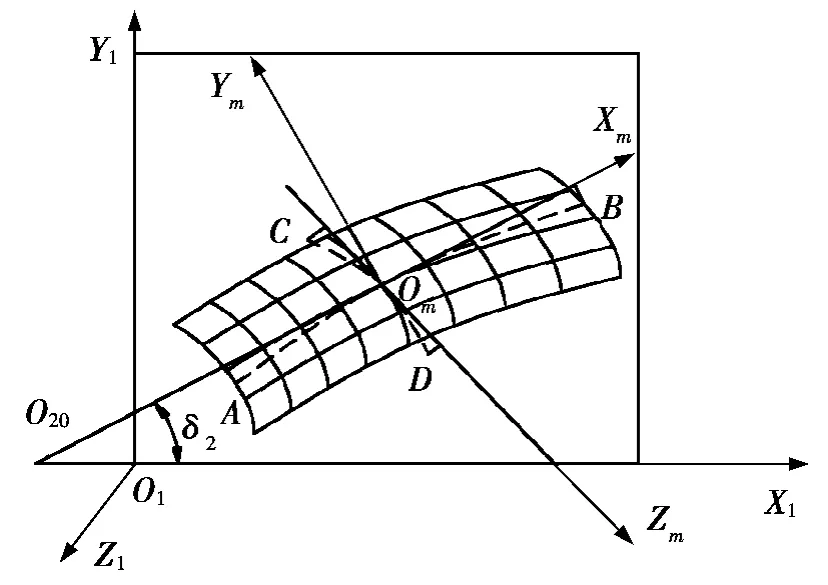
图2 齿面修形坐标系

齿长方向上，在XmOmYm平面内建立抛物线，如图2中AOmB所示，设其方程为

在端点A、B处，设定一个ym值，ym的设定根据准双曲面齿轮的承载啮合仿真确定，保证在齿面承载下有最佳的接触区。根据齿宽得到A、B处的xm值，则可以确定系数a的值。在齿长方向上为九等分，可以计算出每个等分点处xm的值，进而也可以确定每个等分点处的ym值。

齿高方向上，在ZmOmYm平面内建立抛物线，如图2中COmD所示，设其方程为

以节锥线为分界线，分别将齿顶高和齿根高划分为两部分，在C点设定一个yCm值，根据齿顶高和齿根高的已知量，可以确定系数b和D点的yDm值，然后以和齿长方向相同的方法确定每一个等分点的zm值和ym值。yCm和yDm的设定同样根据准双曲面齿轮的承载啮合仿真确定，保证在齿面承载下有最佳的接触区。

在节线方向上和齿宽中线方向，均以每个等分点的ym或zm值为修正量，直接在每个等分点所对应的法矢方向上将原坐标向下变动△r1=ym或△r2=zm。设在坐标系S1中，齿长方向或齿高方向任一点的坐标为(x，y，z)，其对应单位法矢为(cosα1，cosα2，cosα3)，修形之后坐标为(x'，y'，z')，△r在坐标系S1中各个坐标分量上的投影为(△x，△y，△z)，则有

其中，(△x，△y，△z)=(△r cosα1，△r cosα2，△r cosα3)。

上面的推导过程求出了在节线方向上和齿宽中线方向上每一点的修形量和修形后的坐标，在齿面上任一点，设其所对应齿宽中线第i个点所在的行和节线方向上第j个点所在的列，可确定其修正量为

至此，可确定齿面上每个点修形之后的坐标(x'，y'，z')。

3 应用实例的三维仿真及齿面点计算

基于上述修形理论，以z1=6，z2=35中的小轮为例进行计算，齿轮副参数如表1所示。

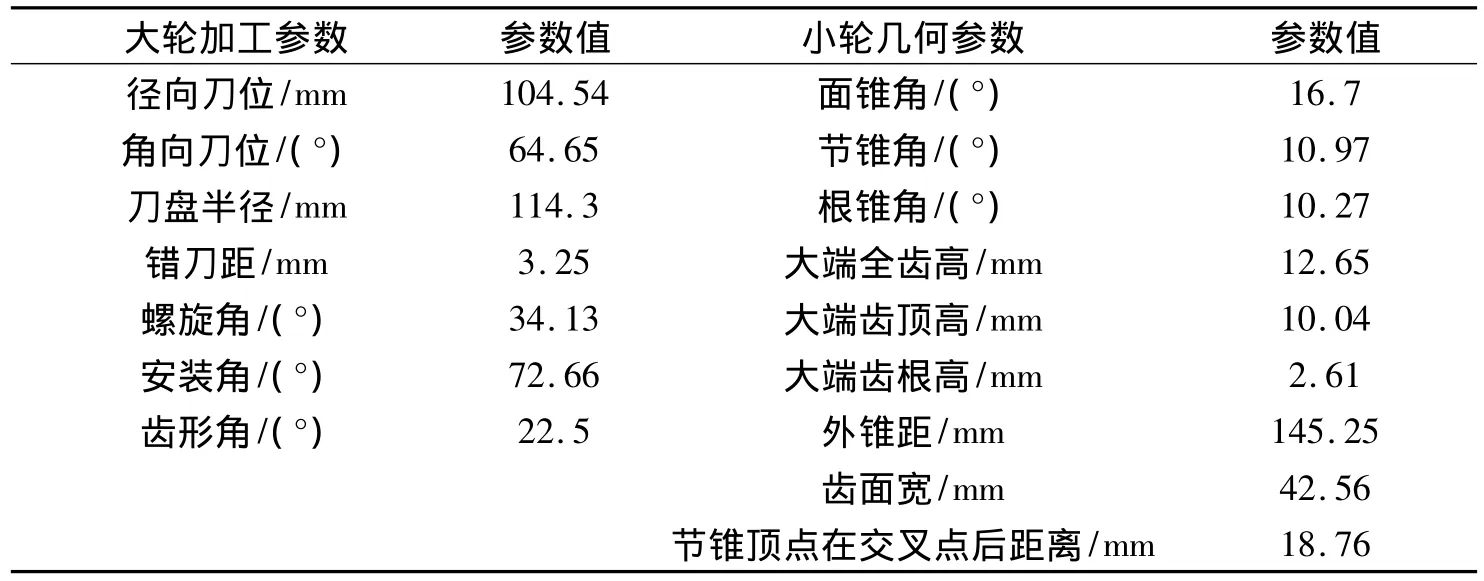
表1 齿轮副参数

对共轭修形齿面点的计算以VC编程软件来实现，在VC中编制相应程序，其界面如图3所示。

图3 小轮齿面点计算

根据承载啮合仿真设定齿长方向最大修形量为0.10 mm，齿高方向最大修形量为0.03 mm，在图3所示的程序界面上输入相应的修形量即可完成齿面点的计算。将所得齿面点导入UG建模软件中，可得修形后齿轮副啮合仿真图及小轮三维模型，如图4和图5所示。

图4 修形后齿轮副啮合仿真

图5 小轮三维模型

4 切齿试验及齿面测量

图6 小轮精加工模型

图7 齿面测量

小轮齿面的加工在FMH-630四轴联动加工中心上进行。根据UG中建立的三维模型，结合FMH-630加工中心特点，建立三维坐标系，生成数控程序并进行后置处理后，分别用半径为3 mm和2 mm的球头铣刀对小轮凹、凸面和齿根过渡曲面进行粗加工和精加工。精加工后的小轮如图6所示。

为了验证齿面主动修形技术的可行性和齿面加工的精确性，在JD45+型齿轮测量中心上对小轮齿面采用点阵式测量［10－11］。选用直径为2 mm的球形测头，在测量软件中设置相应的参数，然后根据5×9点阵由参考点分别向大端和小端进行测量，如图7所示。小轮齿面的测量点和准双曲面齿轮最常用的HFT法(大轮成形法，小轮刀倾法)理论计算齿面进行对比，偏差很小，测量报告如图8所示，具体偏差如表2所示。

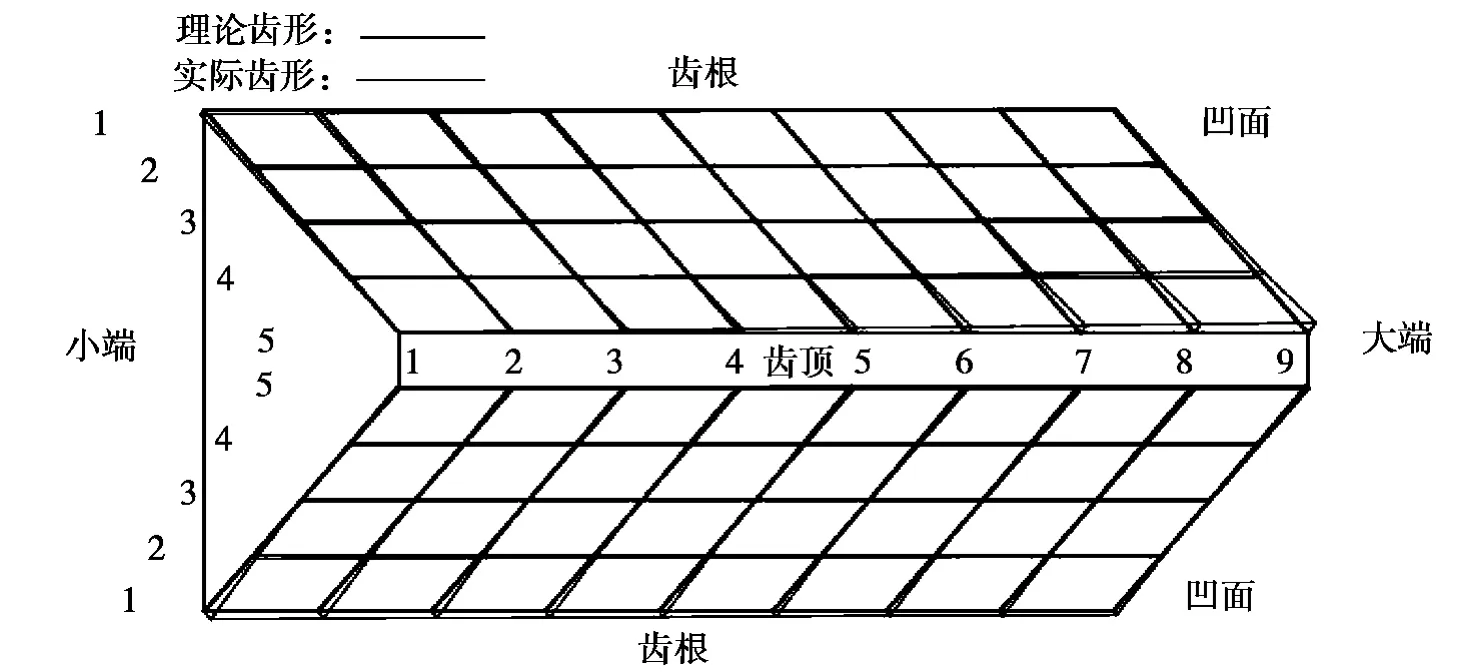
图8 齿面测量结果

从测量结果看，用HFT法计算出的齿面点与在共轭齿面基础上通过抛物线修形得到的齿面相比，凹面最大偏差存在于大端齿顶，为0.081 4 mm，凸面最大偏差存在于小端齿根，为0.071 9 mm。两者压力角和螺旋角均基本吻合，测量结果符合预期目标，验证了齿面点加工的精确性和齿面主动修形技术的可行性。

表2 齿面偏差

5 结论

根据大轮的齿面方程和小轮几何参数，实现了在共轭基础上修形齿面点的计算，通过理论研究对准双曲面齿轮的主动修形理论进行了探讨，在卧式加工中心上进行了小轮的切齿试验，在齿轮测量中心上对齿面的误差进行了测量。测量结果表明:修形效果符合预期目标，验证了本文提出的抛物线型修形理论的正确性。

［1］ Litvin F L.Gear Geometry and Applied Theory［M］.New Jersey:Prentice Hall，1994.

［2］ 曾韬.螺旋锥齿轮设计与加工［M］.哈尔滨:哈尔滨工业大学出版社，1989.

［3］ 杨建军，魏冰阳，周彦伟，等.准双曲面齿轮设计加工集成系统的开发［J］.河南科技大学学报:自然科学版，2004，25 (5):17－20.

［4］ 王利环，魏冰阳.准双曲面齿轮节锥参数设计的新方法［J］.河南科技大学学报:自然科学版，2008，29(2):25－27.

［5］ 吴训成，毛世民，吴序堂.点啮合齿面主动设计理论和方法［J］.机械科学与技术，2000，19(3):347－349.

［6］ 吴训成，毛世民，高本河，等.准双曲面齿轮齿面主动设计与先进制造技术［J］.汽车工程，2001，23(1):30－32.

［7］ 周凯红，唐进元，严宏志.基于预定啮合特性的点啮合齿面设计方法［J］.航空动力学报，2009，24(11):2612－2617.

［8］ 王军，王小椿，姜虹，等.螺旋锥齿轮齿面三坐标测量［J］.机械工程学报，2003，39(6):151－154.

［9］ 蒋闯.准双曲面齿轮数字化制造建模及应力分析的新方法研究［D］.洛阳:河南科技大学，2012.

［10］ 邓效忠，李天兴，李聚波，等.汽车驱动桥准双曲面齿轮齿面测量误差精确计算［J］.中国机械工程，2012，23(12): 1502－1507.

［11］ 汪中厚，周晓玲.汽车驱动桥锥齿轮齿面检测与质量控制［J］.现代零部件，2005，5(11):57－61.